Epidemias

Qué es una epidemia.

El término epidemia (del griego epi, por sobre y demos, pueblo) describe la situación generada por una enfermedad que afecta a un número de individuos superior al esperado durante un período de tiempo.

A lo largo de la Historia, se han conocido muchas epidemias de gran importancia. En la Biblia, son frecuentes las menciones. En el siglo II d.C. las llamadas plagas del reinado de Antonino (posiblemente sarampión y viruela) se expandieron por el Imperio Romano, debilitando al mismo; las victoriosas campañas de Hernán Cortés contra los aztecas y Francisco Pizarro contra los incas estuvieron marcadas por la expansión de la viruela en el continente americano; la peste negra, procedente de Asia, acabó con la vida de millones de personas desde su aparición, en 1346; condujo además a brotes epidémicos recurrentes durante más de 300 años, entre otros la gran peste de Londres (1665–1666) y la plaga italiana (1629–1631).

Se acepta hoy día con gran generalidad que las epidemias han jugado un papel fundamental en el desarrollo histórico de la humanidad.

Algunos modelos simples.

Presentaremos aquí los resultados que producen algunos modelos matemáticos de epidemias. Con frecuencia, éstos permiten explicar y predecir la evolución de las mismas.

El primer intento de modelado se debió a Sir Ronald Ross (1857-1932), que fue introductor e impulsor de la Patometría.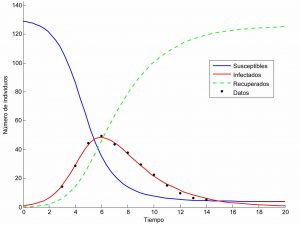

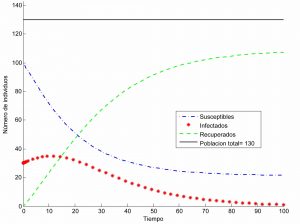
Algo más tarde, en 1927, W.O. Kermack y A.G. McKendrick idearon el modelo SIR, donde se aceptan tres tipos de individuos: susceptibles, infectados y recuperados; sus evoluciones en el tiempo están respectivamente descritas por las funciones \(S = S(t)\), \(I = I(t)\) y \(R = R(t)\), que deben verificar un sistema diferencial no lineal cuyas soluciones están representadas en las gráficas.

Tienen interés (al menos) las dos variantes siguientes del modelo SIR:

(a) el modelo SIRp,  donde se supone que algunos individuos susceptibles nacen y algunos individuos infectados o recuperados mueren a lo largo del tiempo;

(b) el modelo SIRS, en donde, además, los individuos recuperados pueden perder la inmunidad y volver a ser susceptibles.

Otros modelos más complejos

En los modelos SIR y sus variantes, se ha supuesto que la población no está extendida espacialmente y se encuentra bien «mezclada».

Podríamos haber tenido en cuenta también el efecto de la edad, la presencia de sistemas de vacunación y tratamiento, la estructura social de la población, etc.

Naturalmente, todo esto conduce a modelos de mayor complicación, donde determinar el comportamiento de las soluciones puede ser mucho más difícil.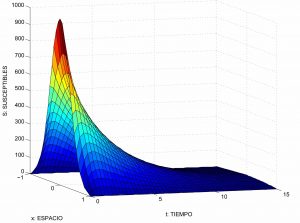

Aceptemos en particular que los individuos susceptibles e infectados están distribuidos a lo largo y ancho de un habitat 1D (un intervalo), respectivamente con densidades de población \(S = S(x,t)\) e \(I = I(x,t)\).

Tiene entonces sentido generalizar el modelo SIR y formular un sistema de ecuaciones en derivadas parciales para \(S\), \(I\) y \(R\).

Para hacerse una idea de las soluciones que se obtienen cuando imponemos que la población total se anula en el borde del hábitat (véase la gráfica a la derecha).

Para saber más

El lector encontrará más información en las referencias siguientes:

[1] Anderson, R.M. May, R.M., Infectious Diseases of Humans. Oxford: Oxford University Press, 1991.

[2] Brauer, F. Castillo-Chávez, C., Mathematical Models in Population Biology and Epidemiology. NY: Springer, 2001.

[3] Daley, D. J. Gani, J., Epidemic Modeling. An Introduction. NY: Cambridge University Press, 2005.

[4] Trottier, H., Philippe, P., Deterministic modeling of infectious diseases: theory and methods. The Internet Journal of Infectious Diseases, 2001. Retrieved December 3, 2007, from https://www.ispub.com/ostia/index.php?xmlFilePath=journals/ijid/volln2/model.xml