La descomposición geométrica de una figura para componer con las piezas otra distinta es un problema matemático con miles de años de antigüedad. Por ejemplo, Stomachion es una palabreja griega que significa «dolor de barriga», pero también es una obra de Arquímedes sobre un juego que consiste en componer cuadrados u otras figuras con las 14 piezas predefinidas en que ha sido dividido un cuadrado.
Más recientemente, en 1833, F. Bolyai, P. Gerwien y W. Wallace demostraron que dados dos polígonos del mismo área puede descomponerse el primero en otros que por traslaciones y giros formen exactamente el segundo. Se dice entonces que los dos polígonos son equidescomponibles.
Si consideramos tres o más dimensiones, tenemos uno de los resultados más sorprendentes de las matemáticas: la paradoja de Banach-Tarski. Es este un resultado tan extraño que aun siendo un teorema lo llamamos paradoja: afirma que casi cualquiera dos conjuntos en el espacio tengan o no el mismo volumen son equidescomponibles (basta, por ejemplo, que contengan una bola y estén contenidos en otra). Esto es, un guisante se puede descomponer en piezas que recompuestas dan como resultado el sol.
La idea básica del teorema de Banach-Tarski es en realidad debida a Hausdorff, quién uso el resultado para demostrar que la medida de volumen no puede definirse para todos los conjuntos del espacio de manera consistente con los axiomas básicos del volumen. Dicho en otras palabras, hay conjuntos tan complicados que no se les puede calcular el volumen, por lo que descompuesto un cuerpo en este tipo de conjuntos la conservación del volumen deja de tener sentido. A estos extraños conjuntos se les llama no medibles.
La geometría del plano, impide sin embargo estas construcciones paradójicas. De hecho, el propio Banach probó que sí es posible definir el área para todos los conjuntos, de manera que en cualquier descomposición de figuras planas se tiene que conservar el área. Teniendo esto en mente, Tarski planteó en 1925 la extensión del teorema de Bolyai-Gerwain-Wallace para cuadrados y círculos: ¿son equidescomponibles un cuadrado y un círculo del mismo área? Esto es, ¿existe un puzle con un número finito de piezas con el que podamos reconstruir un cuadrado y también, colocándolas de otra forma, un círculo? (por el teorema de Banach las dos figuras deben tener el mismo área). A este rompecabezas se le llamó problema de la cuadratura del círculo de Tarski.
El problema de Tarski no tiene relación con el problema clásico de la cuadratura del círculo, que propone construir un cuadrado con igual área que un círculo usando exclusivamente regla y compás. Este problema que data de los griegos fue resuelto negativamente por F. Lindemann a finales del siglo XIX.
En el concepto de conjuntos equidescomponibles juega un papel relevante la mayor complejidad del grupo de los movimientos del espacio respecto a los del plano. Por ejemplo, en el espacio, si consideramos sólo traslaciones, ni la construcción de Hausdorff ni la de Banach y Tarski son ya posibles, y dos conjuntos equidescomponibles por traslaciones necesariamente tienen el mismo volumen. En el plano, la situación es distinta, porque usar sólo traslaciones no limita demasiado nuestras posibilidades. Por ejemplo, como muestra la figura podemos «girar» un cuadrado usando sólo traslaciones:
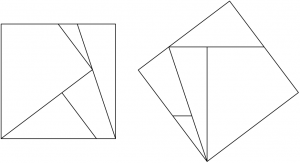
En 1994, el matemático húngaro Mikos Laczkovich resolvió el problema de la cuadratura del círculo de Tarski afirmativamente, demostrando que el círculo podía descomponerse en menos de $latex 10^50$ piezas que mediante traslaciones (únicamente traslaciones) podían reconstruir exactamente un cuadrado.
Esto es sorprendente porque la intuición nos dice que algunas de las piezas deberían tener una curvatura para adaptarse a la forma del círculo, curvatura que debe desaparecer al componer el cuadrado. La importancia de este hecho había sido demostrada en 1963 por Dubins Lester, Morris W. Hirsch y Jack Karush; probaron que (dicho sin mucha precisión) el círculo y el cuadrado no son equidescomponibles con piezas que podamos recortar con unas tijeras (piezas limitadas por curvas de Jordan, si se quiere más precisión). Las piezas en la construcción de Laczkovich necesariamente han de ser difíciles de imaginar.
Por esta razón la pregunta que nos surge de la construcción de Laczkovich, y que él mismo planteó en su trabajo, es si se puede conseguir que las piezas sean medibles. El que las piezas sean medibles les da un grado de realidad. Los conjuntos no medibles nos los impone la lógica, pero no tienen una realidad física. De hecho, el que en la paradoja de Banach Tarski las piezas sean necesariamente no medibles (yo diría que no son de este mundo) le da un carácter extravagante y ajeno a la realidad física. Así que en el caso del plano, quedaba el problema abierto de si podemos cuadrar el círculo con piezas medibles.
Y decimos quedaba, porque se acaba de probar que tal descomposición es posible: hay un número finito de piezas medibles que colocadas de cierta manera componen exactamente un círculo y trasladándolas convenientemente forman exactamente un cuadrado del mismo área –el resultado será publicado próximamente en Annals of Mathematics–.
La demostración se debe a los matemáticos Lukasz Grabowski, András Máthé y Oleg Pikhurko, que trabajan en tres universidades del Reino Unido. Su demostración usa la teoría de grafos y se aplica a situaciones mucho más generales que la del cuadrado y el círculo en el plano.
Para saber más:
Grabowski, A. Máthé, O. Pikhurko, «Measurable circle squaring», Annals of Mathematics, (por aparecer).
S. Wagon, «The Banach-Tarski paradox, Cambridge University Press, Cambridge, 1993.

Dejar una contestacion