Modelos matemáticos de la dinámica de poblaciones: Modelo de Malthus

1.- Introducción del modelo de Malthus

Thomas Robert Malthus nació en 1766 en Surrey, condado del sureste de Inglaterra, Reino Unido. Estudió en el Jesús College de Cambridge, donde cursó estudios en filosofía y teología; hasta que en 1788 se graduó como Ministro Anglicano. A partir de ese año se mantuvo en Cambridge como fellow hasta 1804, año en el se casó, por lo que tuvo que renunciar a su cargo, según las reglas del Jesús College.

En 1798, a sus 32 años, Malthus publicó, anónimamente, un libro titulado An Essay on the Principle of Population (Un Ensayo sobre los Principios de la Población) y del que llegaron a editarse hasta seis ediciones, en las que el autor iba incorporando nuevos datos intentando justificar y argumentar sus postulados. Desde su edición, este libro tuvo una gran repercusión en las ciencias económicas, pero nosotros centraremos nuestra atención en su trascendencia en la dinámica de poblaciones, en demografía.
Malthus quería explicar la razón de la pobreza existente en aquellos tiempos, y formuló una teoría que puede ser resumida de forma simplificada con la siguiente frase: “Cuando no lo impide ningún obstáculo, la población va doblando cada 25 años, creciendo de período en período, en una progresión geométrica. Los medios de subsistencia, en las circunstancias más favorables, no se aumentan sino en una progresión aritmética.” Su visión se basaba en que las mejoras tecnológicas agrícolas y en la producción de alimentos solo conllevaban mejoras temporales ya que serían consumidas por el excesivo aumento de la población.

2.- Catástrofe Malthusiana

Bajo este supuesto, Malthus previno una Catástrofe en el año 1880, ya que si la población crece de forma geométrica y los recursos de forma aritmética, habría un momento donde las personas no tendrían recursos para sobrevivir, vivirían en la miseria. Para evitar tal catástrofe, se pueden proponer varios controles que eviten el crecimiento exagerado de la población. Unos pueden ser intrínsecos (enfermedades, guerras, epidemias, mala alimentación, hambre…) y otros que el propio Malthus sugirió con ahínco (de muy diversos tipos) en el crecimiento demográfico. Propuso, por ejemplo, controles en los nacimientos y reducir o eliminar a los pobres. Tanta repercusión tenían los planteamientos de Malthus, que incluso el gobierno inglés promulgó leyes en contra de la indigencia.
La catástrofe malthusiana no se produjo ya que, por un lado, Malthus no tuvo en cuenta la gran capacidad que ha tenido el hombre para generar alimentos, la tecnología también crece, y por tanto, crecen métodos para desarrollar más alimentos. Y por otro lado, muchas sociedades moderaron su índice de natalidad al alcanzar un mayor nivel de renta.

3.- ¿Puede ser el modelo de Malthus una buena aproximación?

A pesar del fracaso de las previsiones malthusianas, este modelo ha seguido usándose para modelar el comportamiento de algunas especies (por ejemplo, para modelar el crecimiento inicial de bacterias sobre un sustrato rico en nutrientes, donde las bacterias pueden crecer y reproducirse sin restricciones). La ley se puede escribir en términos de ecuaciones diferenciales de la siguiente forma: el crecimiento de una especie es proporcional al número de individuos de la especie; o bien, que la tasa de crecimiento de la especie es constante. Esta suposición hace que la población crezca de forma exponencial, como predijo Malthus, eso sí, con una velocidad constante que en principio es desconocida. Por otro lado, el crecimiento de los alimentos, según proponía el propio Malthus, era constante, con lo que los alimentos crecían de forma lineal.

Claramente el modelo de Malthus es muy simple y poco realista para que recoja el comportamiento complejo de una población. En realidad, según este modelo o una población crecería de forma incontrolada a lo largo del tiempo o decrecería hasta desaparecer la especie.

Evidentemente una de sus grandes limitaciones es que se supone que la tasa de crecimiento de la especie se mantiene constante a lo largo del tiempo, es siempre la misma y no depende de otros factores o recursos, como por ejemplo de la propia especie.

Veamos a continuación varios ejemplos de cómo variaría una población determinada según el modelo de Malthus. Pongamos como ejemplo la población española. En la tabla siguiente mostramos el crecimiento de la población española desde el inicio del siglo XX:

 

1900	1910	1920	1930	1940	1950	1960
18.616.630	19.990.669	21.388.551	23.677.095	26.014.278	28.117.873	30.582.936

 

1970	1981	1991	2001	2006	2008	2014
33.956.047	37.742.561	39.433.942	40.499.791	44.708.964	46.063.511	46.507.760

 

Si tomamos como referencia la velocidad de crecimiento de la población española en los años 70, dicha tasa (calculada ajustando los datos conocidos) es 0.009611040332240, por lo que según la ley de Malthus en 2014 tendríamos una población de 51.829.149 !!! por los 46.507.760 que había según los datos, y una estimación de 118.451.334 de habitantes para 2100.

En la figura superior siguiente comparamos la población real en España desde 1970 y 2014 (expresadas con *) y la estimación con el modelo de Malthus (curva continua). 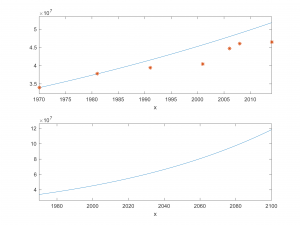En la inferior, se muestra el perfil de la solución hasta el año 2100.

Puede parecer que hemos elegido una etapa en la que en España se produjo el conocido como baby-boom y por tanto la previsión no era la correcta. Sin embargo, si tomamos la velocidad media desde 1900 hasta 1980 de España, 0.007695460854668, se obtiene según el modelo de Malthus una población en el 2014 de 44.761.025….y de 86.760.152 de habitantes en 2100. En la siguiente figura (der.) mostramos de nuevo por una lado (figura superior) la comparación de la población real con la estimación por el modelo de Malthus desde 1900 al 2014. En la inferior se representa dicha estimación hasta el año 2100.

Esto es, incluso teniendo una velocidad de crecimiento calculada, en media, durante un siglo, el modelo deja de ser realista cuando se deja pasar una cantidad de tiempo importante.

Por otro lado, tomando como dato que en el 2013 España tiene una tasa de crecimiento negativa de un -0,2%, la población en los 50 siguientes años seguirá, según la ley de Malthus, la gráfica siguiente:

 

Según esta estimación, si el ritmo de crecimiento negativo se mantiene a lo largo de los años, en el año 2065 habrá en España aproximadamente 42 millones de habitantes.