Solución: Ciudades de Europa

A continuación mostramos la solución al Divertimento Ciudades de Europa. Gracias a Alberto Castaño por su solución.

Divertimento:

En el mapa de Europa conectamos cada ciudad con la que esté más próxima. Si suponemos que las distancias entre ciudades son siempre distintas, mostrar que ninguna ciudad estará conectada con más de cinco ciudades vecinas.

Solución:

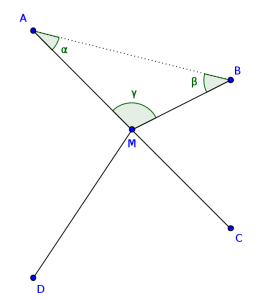
Supongamos que la ciudad \(M\) es la más próxima a las ciudades \(A,B,C,D,E,\ldots\) Se puede suponer que estas ciudades están ordenadas en sentido horario, con centro en \(M\), y comenzando en \(A\).

Tracemos el segmento que une las ciudades \(A\) y \(B\). En el triángulo \(ABM\), el lado mayor es \(AB\); en caso contrario, \(A\) estaría más cerca de \(B\) que de \(M\). Por tanto, \(\gamma > \alpha\) y \(\gamma > \beta\), y se tiene que
$$
3 \gamma > \alpha + \beta + \gamma =180^o.
$$
La desigualdad anterior implica que \(\gamma > 60^o\). El mismo razonamiento se puede hacer para los triángulos \(BCM\), \(CDM\ldots\), con un ángulo en el vértice \(M\) siempre mayor que \(60^o\). Se deduce que, como máximo, son cinco los triángulos con el vértice común en \(M\), es decir, \(M\) no puede ser la ciudad más próxima a más de cinco ciudades.