En la próxima entrega de Divertimentos volvemos al libro One hundred problems in elementary Mathematics, del matemático polaco Hugo Steinhaus (1887-1972). Así que hoy dedicaremos esta entrada a continuar con las historias del Café Escocés (para las dos primeras véanse Historias del Café Escocés: 1. Steinhaus y Banach, Historia del Café Escocés: 2. La tertulia matemática).
Las tertulias matemáticas que el grupo de Banach y Steinhaus celebraban en el Café Escocés de Lwów acabaron trascendiendo el ámbito local hasta llegar a fecundar una parte no despreciable de las matemáticas hechas en el último cuarto del siglo XX.
El portentoso objeto que permitió tal prodigio fue un modesto cuaderno; una simple libreta que se ha acabado convirtiendo en uno de los más célebres y celebrados documentos matemáticos: es el Cuaderno Escocés.
Hay varias versiones para explicar el nacimiento del Cuaderno Escocés. Una dice que dada la intensidad y valor de las discusiones matemáticas que tenían lugar en el Café, y el tiempo que a ellas dedicaban, Banach propuso anotar en un cuaderno las cuestiones y problemas que surgían. Hasta entonces garrapateaban notas en el mármol de las mesas; notas que inevitablemente se llevaba el trapo húmedo que los camareros usaban para limpiar, quedando tan diluidas en el olvido como lágrimas en la lluvia. Pero hay otra versión que dice que el dueño del Café, harto de ver el mármol de sus mesas siempre sucio de garabatos, se quejó a los tertulianos. En vista del poco caso que le hicieron, fue con la queja a la mujer de Banach que, más responsable, acabó comprándoles, por dos złotys y medio, un cuaderno al marido y sus amigos para que apuntaran allí sus cosas.
Ya fuera por un motivo u otro, una tarde Banach se presentó en el Café con un cuaderno sólido y bien encuadernado donde, pocas horas después, anotó de su puño y letra un primer problema que él mismo propuso. Era el 17 de julio de 1935 y, lo que después se ha dado en llamar el Cuaderno Escocés, uno de los documentos matemáticos más importantes del siglo XX, recogía el primero de los 197 problemas que lo componen.
Los problemas no son problemas aptos para no iniciados: digamos que son droga matemática dura; en casi todos ellos se requiere, tan sólo para entender lo que se pregunta, un conocimiento matemático avanzado. Pero hay algún que otro problema que sí puede entender alguien sólo con formación elemental en matemáticas –otra cosa es resolverlo–. Por ejemplo, el número 59, propuesto por Stanisław Ruziewicz, dice: «¿Se puede descomponer un cuadrado en un número finito de cuadrados más pequeños todos ellos diferentes?»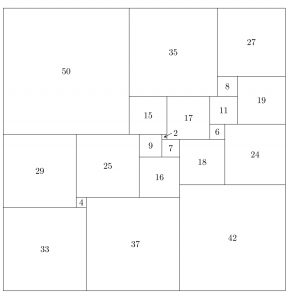 
El problema es endiabladamente complicado y ha dado bastante juego matemático. Por ejemplo, en 1978 se probó que el mínimo número de cuadrados distintos en que se puede descomponer un cuadrado es 21; hay entonces una única posibilidad de hacer la descomposición (ver figura).
Si se quiere un problema de los que he calificado como droga matemática dura bastaría casi con escoger al azar un número del 1 al 197. He aquí, por ejemplo, el 101 –propuesto por Stanisław Ulam–: «Un grupo \(U\) de permutaciones de la sucesión de enteros es llamado infinitamente transitivo si tiene la siguiente propiedad: si \(A\) y \(B\) son dos conjuntos de enteros, ambos infinitos así como sus complementarios con respecto a todos los enteros, entonces existe en el grupo \(U\) un elemento \(f\) (permutación) tal que \(f(A)=B\) . ¿Tiene que ser un grupo infinitamente transitivo necesariamente idéntico al grupo de todas las permutaciones?» La respuesta es negativa.
El Cuaderno Escocés sobrevivió a la guerra. Nuestro Steinhaus le envió a Ulam una trascripción desde Polonia en 1956; Ulam, que trabajaba por entonces en el Laboratorio Nuclear de Los Álamos, lo tradujo al inglés e hizo imprimir algunos centenares de copias pagadas de su propio bolsillo: «Los Álamos –explicó Ulam– es un laboratorio del Gobierno, y uno no puede usar los impuestos de los contribuyentes para propósitos frívolos» –algo de lo que deberían tomar buena nota los políticos corruptos El problema de los políticos corruptos–. De esa edición, llevó ejemplares al Congreso Internacional de Matemáticos que se celebró en Edimburgo en 1958 –los escoceses quedaron un tanto defraudados al saber que el nombre del cuaderno no hacía referencia a Escocia sino a un café de Lwów–. A partir de ahí, el Cuaderno Escocés empezó a ejercer su influencia sobre la comunidad matemática. Desde Los Álamos se enviaron ejemplares de esa impresión, y de otra posterior hecha en 1977, a quien la solicitó. Así siguió distribuyéndose privadamente por universidades de aquí y de allá, hasta que una más cuidada edición, que incluía artículos de algunos protagonistas de la historia, estuvo comercialmente disponible tras el congreso dedicado en Texas en mayo de 1979 a los problemas matemáticos del Cuaderno Escocés. Problemas que han alimentado los desvelos matemáticos de una parte del gremio en el último cuarto del siglo XX –uno de ellos fue resuelto en 1982 por F.J. Freniche, catedrático de matemáticas en Sevilla–; y todavía algunos pocos lo siguen haciendo, pues su solución sigue siendo desconocida.
Referencias
A.J. Durán, Pasiones, piojos, dioses… y matemáticas, Destino, Barcelona, 2009.
Dejar una contestacion