El valor de un trabajo matemático es una cuestión difícil de medir. Hay artículos que resuelven un problema que lleva planteado largos años, como el de Andrew Wiles resolviendo el problema de Fermat. Hay otros increíbles, como el de Viggo Brun, que usaba el método de la criba para acotar el número de primos gemelos. Este trabajo estuvo años en el cajón de Edmund Landau, que cuando lo vio la primera vez pensó: «lo que dice hacer es imposible de hacer». Cuando lo leyó se dio cuenta de que lo imposible no lo era. De este tipo es también el trabajo de Yitang Zhang en el que prueba que hay infinitos pares de primos a una misma distancia \(d\le 7\times10^7\). Los especialistas sabían que estaban cerca de probarlo pero habían considerado la tarea como imposible. Al cabo de unos años llegó Yitang con su ingeniosa prueba para demostrarles que estaban equivocados.
Otra clase de artículos, no dan un resultado nuevo, pero dan una prueba de un teorema conocido que termina por hacer olvidar las anteriores demostraciones. Un ejemplo típico es la prueba del teorema de Goursat en variable compleja.
Alguien dijo que el valor de un trabajo matemático se mide por el número de otros resultados que han necesitado páginas y páginas y que quedan incluidos es un teorema más general y/o con una prueba más simple. El ejemplo típico de este tipo de trabajo es el de finitud de la base en un ideal de polinomios que hizo Hilbert y que hacía obsoleto a todo un enjambre de pruebas de la teoría de invariantes. «Esto no es Matemática, es Teología», exclamó Paul Gordan, cuyos trabajos perdían buena parte de su valor con la prueba de Hilbert.
Algo de este tipo de valor tienen los trabajos en geometría convexa que voy a comentar aquí, obra de Bernardo González Merino y Matthias Henze (y colaboradores). Ver un trabajo de un español hecho en Alemania me da pie para algunas observaciones sobre la matemática española.
Los teoremas de Minkowski.

H. Minkowski, entre otras cosas, fue el creador de la Geometría Convexa, con la que resolvió diversos problemas de Teoría de Números, por ejemplo probó la finitud del número de clases de ideales. Hermite quedó tan impresionado de la lectura del libro de Minkowski, Geometrie der Zahlen, que exclamó «creo que he visto la tierra prometida».
Minkowski considera conceptos como el de cuerpo convexo simétrico y el de retículo.
Un conjunto \(K\) es convexo si contiene para cualesquiera dos puntos de \(K\) el segmento que los une.
\(K\) es simétrico si tiene un centro \(O\) tal que si \(P\) es un punto de \(K\) entonces el punto simétrico \(-P\) respecto de \(O\) también está en \(K\).
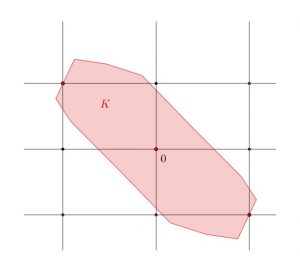
El retículo \(\Bbb Z^n\) está constituido por los puntos de coordenadas enteras. Para cada cuerpo convexo \(K\) denotamos por \(\text{vol}(K)\) su medida en el espacio ambiente, el área si es una figura plana, el volumen si está en el espacio ordinario. También se denota por \(G(K)\) el número de puntos del retículo \(\Bbb Z^n\) que están en \(K\).
Hay dos teoremas básicos debidos a Minkowski. El primero afirma que el volumen del cuerpo \(K\) es menor que \(2^n\) si \(G(\text{int}(K))=1\), esto es, si el centro de simetría \(O\) es el único punto del retículo en el interior de \(K\). En dimensión \(n=2\), el caso extremo lo ilustra el cuadrado de la figura.
El segundo teorema afirma que, en las mismas condiciones, si \(G(\text{int}(K))=1\), entonces el número de puntos en la frontera de \(K\) es \(\le 3^n-1\).

Los resultados de González y Henze extienden el segundo teorema de Minkowski. Bernardo González Merino es español, formado en la Universidad de Murcia, pero actualmente en la Universidad Técnica de Múnich. Sus resultados, realmente interesantes, están contenidos en los artículos:
B. González Merino y M. Henze, A Generalization of the discrete version of Minkowski’s fundamental theorem, Mathematika 62 (2016) 637-652.
G. Averkov, B. González Merino, M. Henze, I. Paschke y S. Weltge, Tight bounds on discrete quantitative Helly numbers, https://arxiv.org/abs/1602.07839.
De van der Corput a la Combinatoria aditiva.
El primer teorema de Minkowski había sido generalizado por van der Corput en 1936. Probando que para cada cuerpo convexo simétrico respecto a un punto reticular \(K\) se tiene
$$\text{vol}(K)\le 2^{n-1}(G(\text{int}(K))+1),$$
siendo \(G(\text{int}(K))\) el número de puntos del retículo en el interior de \(K\).
El teorema que demuestran González y Henze obtiene la correspondiente generalización del segundo teorema de Minkowski, que todavía no se había obtenido. Encuentran la cota óptima del número \(G(K)\) de puntos del retículo en \(K\) en función de los puntos en el interior
$$G(K)\le 3^{n-1}(G(\text{int}(K)+2),$$
determinando también todos los cuerpos convexos extremales que hacen la desigualdad una igualdad.
Lo que me ha impactado de este resultado es como lo transforman en uno de combinatoria aditiva. El punto clave o lema básico es probar que si \(U\) es un conjunto de \(k\) puntos en \(\Bbb R^n\) (\(n\ge2\)), entonces el cardinal del conjunto de las diferencias de puntos de \(U\) es mayor o igual a \(3k-3\) si \(k\) es par o mayor o igual a \(3k-2\) cuando \(k\) es impar. En los casos de igualdad en estos teoremas los puntos del conjunto \(U\) están contenidos en retículos.
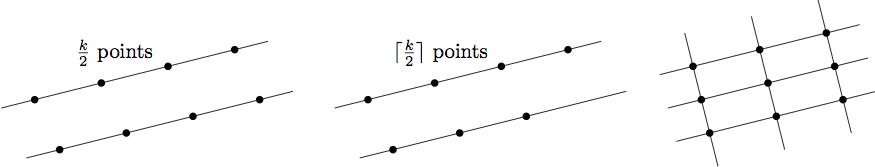
La prueba del teorema usa este lema básico de Combinatoria Aditiva junto con razonamientos de congruencia módulo 3 de las coordenadas de los puntos del retículo contenidos en el interior del cuerpo convexo.
Para encontrar este resultado han debido cambiar el chip. Del retículo \(\Bbb Z^n\) pasan a un conjunto discreto \(S\). Del cuerpo convexo a la envolvente convexa de un conjunto finito de puntos de \(S\), un polítopo con vértices en \(S\). En sus palabras: «[Este marco] exhibe el nivel de generalidad correcto para encontrar las pruebas en el modo más sistemático y conveniente».
Este cambio de chip es una de las aportaciones importantes del trabajo. Este nuevo marco les permite introducir nuevos conceptos en geometría convexa. Consideran para cada número entero positivo \(k\) el número máximo de vértices \(g(S,k)\) de un polítopo que tenga \(k\) puntos adicionales en \(S\). Con esta nueva herramienta resuelven algunos problemas en geometría convexa relativos a los números de Helly.
Sus nuevas técnicas, refinadas en el segundo artículo citado, permiten dar pruebas simples y unificadas de numerosos teoremas previos. Entre ellos el mismo segundo teorema de Minkowski o la prueba del teorema de Doignon: si la intersección de un número cualquiera de cuerpos convexos no contiene ningún punto del retículo \(\Bbb Z^n\), entonces la intersección de \(2^n\) de estos cuerpos convexos tampoco contienen ningún punto de \(\Bbb Z^n\).
En este sentido, tienen valor matemático similar a la demostración de Hilbert de la finitud de la base en un ideal de polinomios (comentado arriba).
Sobre la matemática española y su situación actual.
Me viene a la mente el resumen que Echegaray hizo de su discurso a la Academia:

La ciencia matemática nada nos debe: no es nuestra; no hay en ella nombre alguno que labios castellanos puedan pronunciar sin esfuerzo. (Echegaray, 11 de marzo de 1866).
Durante mi vida he ido viendo cambiar esto. Después de siglos de espera, al fin parecía que iban surgiendo brotes verdes por toda la geografía española. España a la vez iba cambiando, de un país insoportable a uno moderno y activo. ¡Cuántas esperanzas al entrar en Europa! Íbamos a ser como Francia, Alemania, Inglaterra, …
Cada día veíamos nuevos trabajos matemáticos de españoles. ¡Cómo hubiera disfrutado Echegaray al verlo!
Pero un banco en Estados Unidos quebró. Los capitales mundiales temblaron y su miedo se transmitió a Europa. Políticas erróneas de austeridad fueron aplicadas en los países del sur. Y todo lo que se había construido está desintegrándose en apenas tres o cuatro años, sin que el Gobierno parezca reaccionar.
Veo la Matemática Española como un terreno en que hemos ido sembrando y en el que al fin vemos aparecer los primeros brotes de césped, todos sabemos que estos brotes son delicados, que necesitan unos cuidados para que formen una trama que pueda sostenerse. Hay que regarlos regularmente.
Solo con esos cuidados conseguiremos situarnos en el lugar en que siempre debimos estar. Pero se ha vuelto a lo de siempre, a la España insoportable. Se ha recortado justo lo que no debió tocarse, lo que nos podía sacar de la crisis. Nuestras universidades han dejado de absorber a nuestros mejores investigadores. Hoy día los vemos en Universidades de Francia, Alemania, Inglaterra, Estados Unidos, … Personas formadas en España dan sus frutos en otros lugares.
¡Qué ceguera de las autoridades no permitiendo que entren los jóvenes que han demostrado su capacidad! Tanto siglos de espera para que cuando lo teníamos casi a la mano lo tiramos como algo inservible.
El problema no es solo de las Matemáticas, aunque en este caso es mas intolerable por lo poco que costaría mantener la investigación matemática. Voy a aprovechar para enlazar la carta de Amaya Moro Martín investigadora Ramón y Cajal que con amargura se queja antes de volver a la Nasa.
… and when I emigrate shortly, the science I will do will no longer be Spanish, nor thanks to Spain; rather I will keep doing science in spite of Spain.
La beca postdoctoral de Bernardo González Merino en Múnich acababa estos días y su situación se tornaba muy preocupante, con el paro como amenaza. Afortunadamente, acaba de ser contratado como Profesor Ayudante en el Centro Universitario de la Defensa en San Javier. Todavía estamos a tiempo de rectificar, como lo demuestra el caso de Bernardo. Lo tenemos al alcance de la mano.

Dejar una contestacion