Solución: Abrazos en una fiesta

Publicamos la solución al divertimento Abrazos en una fiesta. Gracias a Xavi Martí, Enrique Delgado, Alba González, Rafael Jiménez (alumno del Doble Grado en Física y Matemáticas de la US), Abraham del Valle (alumno del Doble Grado en Física y Matemáticas de la US), Mari Carmen Domínguez, Cartesiano y Miguel Pavón por las soluciones que han aportado.

Además, Alberto Castaño nos ha enviado una solución más general: en las condiciones del problema, si Pepe y Pepa invitan a m parejas, entonces Pepa necesariamente abraza a m invitados.

Divertimento:

Pepe y Pepa dan una fiesta en su casa e invitan a otras 4 parejas. Al llegar, cada persona abraza a todas las otras que conoce, aunque nadie abraza a su pareja y nadie abraza más de una vez a otra persona. Al final de la fiesta, Pepe pregunta a Pepa y a cada uno de sus ocho invitados cuántos abrazos ha dado y obtiene nueve respuestas diferentes. ¿A cuántas personas abrazó Pepa?

Solución:

Dado que son 4 parejas invitadas y que hay que contar a Pepe y a Pepa, tenemos 10 personas en la fiesta. Por tanto, procedemos a modelizar el problema, es decir, a representar los datos del enunciado, por medio de los grafos. En este caso, asignamos un vértice a cada una de las 10 personas y las aristas representarán los abrazos que da cada uno. Denotaremos a los 10 vértices por P0, P1,…, P8 (uno de los cuales tiene que representar a Pepa) y el propio Pepe.

Como sabemos que son 9 las respuestas distintas que recibe Pepe, las denotaremos por 0, 1, 2,…, 8. Vemos que entre las posibles respuestas descartamos el que una persona haya abrazado a 9 personas, pues eso implicaría que esa persona habría saludado también a su pareja.

Llamaremos P0 al asistente que no haya dado ningún abrazo, P1 al que solo haya dado un abrazo, P2 al que solo haya dado 2 y así hasta el P8, que habrá dado 8 abrazos.

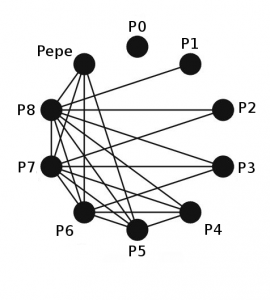
Se tiene entonces este grafo:

Ahora, viendo el grafo, nos centramos en la adyacencia de cada vértice, ya que una característica de cada pareja es que las dos personas que la forman no se abrazan entre sí, es decir, que los vértices correspondientes a cada una de ellas no son adyacentes.

Sabemos que P8 abraza a 8 personas (que no pueden ser ni su pareja ni él mismo), luego el único vértice no adyacente con él (es decir, al único invitado al que quien dio 8 respuestas no ha abrazado) es P0 (que no ha dado ningún abrazo). Por tanto, P0 es la pareja de P8.

P7 abraza a 7 personas, que no pueden ser ni él mismo, ni su pareja, ni P0. Por tanto, P7 es pareja de P1 (que ya había abrazado a P8).

Análogamente, P6 sólo puede ser pareja de P0, P1 y P2 y como los dos primeros ya están emparejados, resulta que P6 es pareja de P2.

Continuando con este razonamiento, deducimos que P5 es la pareja de P3 y que P4 tiene que ser necesariamente Pepa, la pareja de Pepe.

Por tanto, Pepa dio 4 abrazos.