A veces les digo a mis alumnos que si yo tuviera su edad me dedicaría a estudiar desde ya las formas modulares. Son el gran motor de las matemáticas de hoy día. Donde residen las preguntas mas misteriosas. Lo llenan todo. No creo que muchos me hayan hecho caso, no hay un sólo curso sobre formas modulares en Sevilla, y yo a lo más algún año he conseguido dedicarle dos o tres clases.
El problema de Kepler.
Hace unos meses Maryna Viazovska sorprendió a todos con la solución del problema de empaquetamiento de esferas en dimensión 8, a las pocas semanas, usando sus métodos ella y otros cuatro colaboradores Harvey Cohn, Abhinav Kumar, Stephen D. Miller y Danylo Radchenko resuelven el caso de dimensión 24.
El problema se remonta a Kepler quién en 1611 se preguntaba por la mejor forma de empaquetar esferas en el espacio ordinario.
En general en dimensión \(d\), dado un conjunto discreto de puntos \(X\subset\mathbf{R}^d\) tales que la distancia \(d(x,y)\) entre dos puntos distintos de \(X\) sea siempre \(\ge2\), se considera el conjunto \(P=\bigcup_{x\in X}B(x,1)\) formado por las bolas con centro en los puntos de \(X\) y radio \(1\). Estas bolas son disjuntas y se dice que \(P\) es un empaquetamiento de bolas. Su densidad \(\Delta_P\) se define como el límite superior de los cocientes de las medidas cubiertas por las bolas
$$\Delta_P:=\limsup_{r\to+\infty}
\frac{\mathop{\rm Vol}(P\cap B(0,r))}{\mathop{\rm Vol}(B(0,r))}$$
Es decir \(\Delta_P\) mide la proporción de espacio recubierto por las bolas.
Nuestro problema es calcular \(\Delta_d\), es decir, el supremo de esas densidades \(\Delta_d=\sup_P \Delta_P\) cuando las bolas están en dimensión \(d\). Se sabe que esta densidad suprema se alcanza, es decir es un máximo.
Avances sobre el problema de Kepler.
Dimension 1, \(\Delta_1=1\).
En dimensión 1 el problema es trivial. Las bolas son segmentos y se pueden disponer ocupando todo el espacio \(\mathbf{R}\).
Dimension 2, \(\Delta_2=\frac{\pi}{\sqrt{12}}\).
En este caso desde la antigüedad se sospechaba que la mejor densidad está dada por la familiar disposición hexagonal en que cada disco toca a otros seis
Sin embargo, la primera prueba de que \(\Delta_2=\pi/\sqrt{12}\) no fue dada hasta 1910 por A. Thue. Algunos expertos la consideraban incompleta y la primera prueba rigurosa fue dada por L. Fejes Tóth en 1943.
La dificultad es demostrar que ninguna otra disposición de las discos puede dar una densidad mayor.
Dimension 3, \(\Delta_3=\frac{\pi}{\sqrt{18}}\).
En dimensión 3 el problema es mucho más complicado. En 1611 Johannes Kepler en su obra Sobre el copo de nieve hexagonal conjeturó que la mejor forma de empaquetar esferas era el usual en las fruterías para exponer naranjas, con una densidad de \(\frac{\pi}{\sqrt{18}}\). Esta conjetura de Kepler ha tenido una historia muy interesante. La prueba fue publicada por T. Hales en 1998.
T. Hales envió su prueba a la revista Annals of Mathematics. La prueba era poco usual. Recordar que se trata de probar que ninguna otra configuración que la conjeturada proporciona una mayor densidad. Era una prueba por casos que ocupaba unas 250 páginas, aparte de los códigos necesarios para comprobar ciertas desigualdades por ordenador. Annals seleccionó como referees un grupo de 12 matemáticos. Después de cuatro años, este equipo dirigido por Fejes Tóth anunció que no habían encontrado errores en la prueba, aunque no podían garantizar completamente que no hubiera alguno, sobre todo en los códigos.
Finalmente Annals publicó la prueba. La historia no acaba aquí. En el año 2015 T. Hales junto con 21 coautores han publicado una prueba formal completa de la conjetura de Kepler. Esta puede ser comprobada por software de pruebas automáticas.
Las dimensiones \(d=1\), \(d=2\) y \(d=3\) eran los únicos valores exactos conocidos antes del trabajo de Maryna. Maryna ha probado que \(\Delta_8=\pi^4/384\) y con sus colaboradores ha probado también \(\Delta_{24}=\pi^{12}/12!=\pi^{12}/479001600\).
Resultados previos al trabajo de Maryna.
El trabajo de Maryna descansa en dos pilares. Primero: en ciertas dimensiones se dispone de un empaquetamiento especialmente bueno. Esto proporciona cotas inferiores para \(\Delta_d\), inferiores porque no sabemos de cierto que den el empaquetamiento óptimo. Estos empaquetamientos corresponden a retículos \(\Lambda\). Es decir los centros de las bolas están situados en las combinaciones lineales con coeficientes enteros de un conjunto de vectores básicos.
Segundo: Razonamientos de H. Cohen y N. Elkies proporcionan una cota superior.
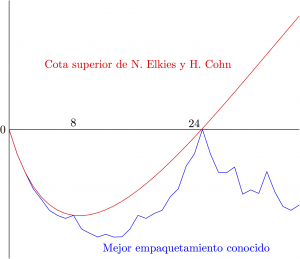
Después de probar este principio H. Cohn y N. Elkies buscan funciones adecuadas que den cotas mejores que las conocidas. En la figura vemos la gráfica de sus cotas superiores frente a las mejores cotas inferiores obtenidas de empaquetamientos particulares.
Elkies y Cohn vieron que, como vemos en la figura, sus cotas eran muy próximas a la cota inferior en el caso de las dimensiones 8 y 24. La igualdad en el razonamiento anterior implicaría que en la sumas de Poisson anteriores todos los términos salvo el correspondiente al origen son \(=0\) para \(f\) y para \(\widehat{f}\).
Esto les hizo conjeturar que habría unas funciones mágicas que darían justamente la igualdad con los mejores empaquetamientos conocidos, que estaban asociados a dos retículos muy famosos por sus propiedades de simetría. Tanto que aunque no pudieron encontrar estas funciones mágicas, estaban tan seguros de encontrarlas en un futuro que titularon su trabajo New upper bounds on sphere packings. I. Pero no pudieron publicar la continuación II.
Maryna y las formas modulares.
Las formas modulares son unas funciones holomorfas definidas en el semiplano superior con dos caras
- Tienen infinitas simetrías asociadas a la geometría no euclídea cuando se consideran como funciones de la variable \(\tau\)
- Tienen un desarrollo en serie de potencias \(\sum a_nq^n\) en la variable \(q=e^{2\pi i\tau}\) cuyos coeficientes \(a_n\) encierran propiedades aritméticas muy interesantes.
Para el que quiera saber más puede empezar mirando los vídeos de las conferencias de Don Zagier que pongo al final de esta entrada. Don Zagier es el director de tesis de Maryna. Ya sabemos dónde encontró las herramientas necesarias para encontrar la función mágica.
Las formas modulares están asociadas muy estrechamente a los retículos, lo que puede hacer sospechar su relación con las funciones mágicas de Cohn y Elkies.
Sin embargo, no era fácil encontrarlas, basta pensar que Elkies debió de intentarlo. (El que no lo conozca puede buscar sus intervenciones en MathOverflow para quedar atónito cada día). Esto hace mucho más meritoria la tarea que ha realizado Maryna.
Maryna Viazovska nació en Ucrania en 1984. Estudio en Kiev y se doctoró en Bonn bajo la dirección de Don Zagier (Modular forms and Special Cycles). Por este trabajo ha recibido el Salem Prize, pero además tiene trabajos importantes anteriores en diseños esféricos.
Para saber más.
[1] El artículo de Maryna tiene una excelente introducción que hemos usado en nuestra exposición:
M. Viazovska, The sphere packing problem in dimension 8. Ann. of Math. 185 (2017), 991–1015.
también lo puedes encontrar en arXiv.
[2] Hemos usado también ampliamente del artículo de divulgación (algo mas explícito que el nuestro) en el Notices de la AMS:
H. Cohn, A Conceptual Breakthrough in Sphere Packing, Notices Amer. Math. Soc. 64 (1917), 102–115.
[3] Otro artículo interesante sobre el tema con entrevista a H. Cohn, Abhinav Kumar, Stephen D. Miller y MarynaViazovska apareció en la revista holandesa Nieuw Archief voor Wiskunde
[4] Para los que quieran mas sobre formas modulares recomiendo las cuatro conferencias de Don Zagier sobre las formas modulares en el International Centre for Theoretical Physics: The Magic of Modular Forms
[4a] Classical Modular formas and some of their applications in arithmetic.
[4b] Modular forms, differential equations and the irrationality of zeta.
[4c] Quasimodular forms and counting problems in topology and group theory.
[4d] Mock modular forms and the string theory of black holes.
Otras cosas mas ligeras:
[5] Un vídeo de Youtube para entender las esferas en dimensión grande.
[7] Articulo en Quanta magazine.




Dejar una contestacion