Solución: Mándala

Publicamos la solución al Divertimento Mándala. En esta ocasión, Rafael Jiménez, Abraham del Valle (alumnos de la Facultad de Matemáticas), Jennifer García y Cartesiano Caótico han propuesto soluciones correctas.

Divertimento:

Un mándala está formado por un cuadrado y cuatro circunferencias centradas en los vértices cuyos radios son el lado del cuadrado. Esas cuatro circunferencias se cortan en 12 puntos, 4 de los cuales están en el interior del cuadrado, 4 están fuera de él y los otros cuatros son los vértices del mismo.

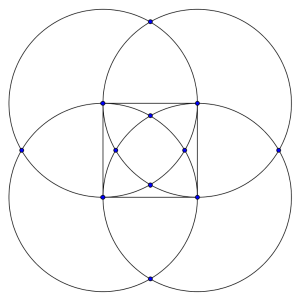
En esos 12 puntos se desean colocar 12 números consecutivos de modo que:

1. Los números colocados en cada circunferencia sumen 63.

2. En el interior del cuadrado estén los dos mayores y los dos menores, con el mayor arriba y el menor a la izquierda.

3. De los restantes números, el mayor debe estar a la derecha y el menor abajo.

4. De los restantes números, los pares deben estar en los vértices superiores del cuadrado y los impares en los inferiores.

Obtén todas las soluciones que hay.

Solución:

Cada punto está situado en dos circunferencias. Si sumamos los números situados sobre cada una de ellas, obtenemos el doble de la suma de todos los números que hemos puesto, de modo que dicha suma es \(63 \cdot 2 = 126\). Así, \(n + (n+1)+ \ldots + (n +11) = 126\), de donde \(n=5\). Los números a colocar son 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 y 16.

Con la notación del dibujo, los números situados en cada circunferencia son: 
 

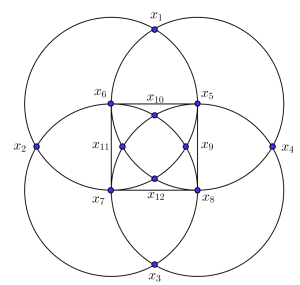
C1: \(x_1, x_2, x_5, x_7, x_9, x_{12}\)

C2: \(x_1, x_4, x_6, x_8, x_{11}, x_{12}\)

C3: \(x_2, x_3, x_6, x_8, x_{9}, x_{10}\)

C4: \(x_3, x_4, x_5, x_7, x_{10}, x_{11}\)

La condición del problema sobre la igualdad de las sumas de los números situados en cada circunferencia implica que

$$x_1+ x_2+ x_5+ x_7+ x_9+ x_{12}=x_1+ x_4+ x_6+ x_8+ x_{11}+ x_{12}$$

$$ x_1+ x_2+ x_5+ x_7+ x_9+ x_{12} =x_2+ x_3+ x_6+ x_8+ x_{9}+ x_{10}$$

$$x_1+ x_2+ x_5+ x_7+ x_9+ x_{12}=x_3+ x_4+x_5+ x_7+ x_{10}+ x_{11} $$

Con los cambios de variable \(y_1=x_1+x_{12}\), \(y_2=x_2+x_9\), \(y_3=x_3+x_{10}\), \(y_4=x_4+x_{11}\), \(y_5=x_5+x_7\), \(y_6=x_6+x_8\), resulta

$$y_2+y_5=y_4+y_6$$

$$y_1+y_5=y_3+y_6$$

$$y_1+y_2=y_3+y_4$$

De estas identidades se deduce que

$$y_1=y_3, y_2=y_4, y_5=y_6.$$

Las condiciones del problema obligan a asignar los números 5, 6, 15 y 16 a las incógnitas \(x_9, x_{10}, x_{11}, x_{12}\), de forma que \(x_{10}=16\) y \(x_{11}=5\). Así, \(x_9\) y \(x_{12}\) son 6 y 15 en algún orden, y el resto de las incógnitas los números comprendidos entre 7 y 14, que se diferencian como máximo en 7 unidades. Ello hace que las ecuaciones

$$ y_1=y_3, \qquad x_1+x_{12}=x_3+16, \qquad x_1-x_3=16-x_{12},$$

$$ y_2=y_4, \qquad x_2+x_9=x_4+5, \qquad x_2-x_4=5-x_9.$$

no pueden tener solución si el segundo miembro es 10 o 11. Por tanto, \(x_{12}=15\), \(x_9=6\).

Así, asignando \(x_{10}=16, x_{12}=15, x_9=6, x_{11}=5\), resultan para las otras incógnitas las ecuaciones

$$ x_1+15=x_3+16,$$

$$x_2+6=x_4+5,$$

$$x_5+x_7=x_6+x_8.$$

La segunda condición obliga a que \(x_4={14}\) y\(x_3=7\), de donde \(x_1=8\) y \(x_2=13\).

Quedan por colocar los números 8, 9, 10 y 11. La última igualdad y la tercera condición obligan a que \(x_5\) y \(x_6\) sean 10 y 12 en cualquier orden y \(x_7\) y \(x_8\) vienen ya determinados. Así, hay dos soluciones, siendo en ambas

$$x_1=8, x_2=13, x_3=7, x_4=14, x_9=6, x_{10}=16, x_{11}=5, x_{12}=15,$$

y teniendo una $$x_5=12, x_6=10, x_7=9, x_8=11,$$ y la otra $$ x_5=10, x_6=12, x_7=11, x_8=9.$$