Cálculo de \(\pi(x)\).
Los griegos probaron que existen infinitos primos. Desde ese momento surgió la pregunta de cuántos de ellos hay hasta un límite dado. Por ejemplo con la criba de Eratóstenes es fácil ver que hasta 100 hay justo 25 primos.
Pero dado un número grande \(x\), ¿cuántos primos hay menores o iguales a \(x\)?
Este número lo designamos por \(\pi(x)\). Por ejemplo \(\pi(10)=4\), \(\pi(100)=25\). A lo largo de la historia se han desarrollado varios métodos para el cálculo exacto de \(\pi(x)\); en cierta forma, ese problema se ha convertido en un campo de batalla donde han competido dos ramas tan distintas de las matemáticas como la combinatoria y el análisis.
Meissel y el método combinatorio.
Legendre en 1808 transformó la criba de Eratóstenes en una fórmula
$$\pi(x)-\pi(\sqrt{x})+1=\lfloor x\rfloor-
\sum_{p\le\sqrt{x}}\Bigl\lfloor\frac{x}{p}\Bigr\rfloor
+\sum_{p<q\le\sqrt{x}}\Bigl\lfloor\frac{x}{pq}\Bigr\rfloor+\cdots$$
y tuvo la paciencia de calcular \(\pi(10^6)\), obtuvo \(78\,526\) en lugar del correcto \(=78\,498\), esto nos indica algo de la dificultad de calcular \(\pi(x)\). Las tablas de primos del momento indicaban \(78\,492\) primos \(\le 10^6\).
Meissel fue el primero en dar un método práctico de calcular valores de \(\pi(x)\) para \(x\) grandes. En 1870 con su método calculó \(\pi(10^8)=5\,761\,455\) primero con un error de \(5\) y después en 1882 exactamente. Debemos tener en cuenta que los cálculos debían realizarse a mano y aunque el método mejoraba mucho sobre el de Legendre la cantidad de cálculos no era despreciable.
Meissel calculó también \(\pi(10^9)\) aunque el valor que obtuvo era realmente \(\pi(10^9)-56\). Sobre este resultado, Lehmer dijo unas décadas después: «El cálculo de Meissel de \(\pi(10^9)\), realizado entre 1871 y 1885, debe ser considerado como uno de los más sobresalientes cálculos del siglo XIX, aunque el resultado sea ligeramente erróneo».
El método de Meissel-Lehmer es una modificación de la fórmula de Legendre, en su forma más simple consiste en escribir
$$\pi(x)=\phi(x,c)-1+c-P_2(x,c)$$ donde \(c=\pi(x^{1/3})\) y \(\phi(x,c)\) denota el número de números \(\le x\) que no son divisibles por ninguno de los primeros \(c\) números primos (es decir el número de los números \(\le x\) cuyos factores primos son todos \(>x^{1/3}\)) y \(P_2(x,c)\) denota el número de productos \(pq\le x\) de dos primos mayores que \(x^{1/3}\). A continuación uno debe calcular \(\phi(x,c)\) y \(P_2(x,c)\).
El cálculo de \(\phi(x,c)\) se hace mediante la recurrencia
$$\phi(x,c)=\phi(x,c-1)-\phi(x/p_c,c-1)$$
donde \(p_c\) es el primo \(c\)-ésimo. Esto conduce a una proliferación de términos que deben calcularse adecuadamente para no sobrecargar mucho la memoria y el tiempo de ejecución. El cálculo de \(P_2(x,c)\) se hace por medio de un método de criba.
Para números \(x\) mayores es preferible usar \(a=\pi(x^{1/4})\) en lugar de \(c\), lo que complica el método.
Primeros ordenadores y avances del método combinatorio.
Con la llegada de los primeros ordenadores llegó la posibilidad de ampliar los cálculos de Meissel. Lehmer,
usando uno de los primeros (un IBM-701, todavía de los que usaban válvulas de vacío con filamento incandescente en lugar de transistores) consiguió calcular \(\pi(10^9)=50\,847\,534\) y \(\pi(10^{10})=455\,052\,511\). El primero corregía el valor erróneo de Meissel, el segundo a su vez tenía un error de una unidad.
Lehmer modificó el método, de forma que se habla del método de Meissel-Lehmer.
Con los ordenadores aparecen también las estimaciones de la efectividad de los algoritmos. Por ejemplo el método de Eratóstenes es poco eficiente. Necesita espacio para \(x\) números, y si contamos las operaciones que debemos realizar con estos números son del orden de \(x\log\log x\), decimos que necesita un tiempo \(O(x\log\log x)\) y un espacio \(O(x)\).
El método de Meissel es difícil de estimar, puesto que usa elecciones de un humano para seleccionar ciertos parámetros. En 1984 Miller, Lagarias y Odlyzko mejoraron teóricamente el método de Meissel-Lehmer obteniendo un método que calcula \(\pi(x)\) usando \(O(x^{1/3+\varepsilon})\) de espacio y \(O(x^{2/3+\varepsilon})\) de tiempo.
Primeros pasos del método analítico.
El origen del método analítico para el cálculo de \(\pi(x)\) está en el artículo de Riemann sobre la función zeta. Es claro que el objetivo de Riemann era fundamentar la sospecha de Gauss de que la diferencia $$\pi(x)-\int_2^x\frac{dt}{\log t}$$
era muy pequeña. Riemann no había terminado sus investigaciones y se había encontrado con la dificultad de probar lo que hoy se conoce como hipótesis de Riemann. Sin embargo, de palabra comunicó a los matemáticos en Berlin que podía dar una fórmula exacta para \(\pi(x)\). Kronecker le pidió vivamente que le mostrara la fórmula y Riemann dio una charla sobre el tema en Berlin. El artículo que conocemos es el resumen de esa charla.
En este trabajo Riemann da una fórmula para
$$\Pi(x)=\pi(x)+\frac12\pi(x^{1/2})+\frac13\pi(x^{1/3})+\cdots$$
lo que para calcular \(\pi(x)\) es igualmente útil. La fórmula es
$$\Pi(x)=\frac{1}{2\pi i}\int_{a-i\infty}^{a+i\infty}
\log\zeta(s)\frac{x^s}{s}\,ds$$
$$=\textrm{Li}(x)-\sum_\alpha\bigl(\textrm{Li}(x^{\frac12+i\alpha})+\textrm{Li}(x^{\frac12-i\alpha})\bigr)+\int_x^\infty\frac{1}{t^2-1}\frac{dt}{t\log t}-\log2.$$
Aquí \(\textrm{Li}(x)\) es una versión del logaritmo integral de Gauss.
En 1982 Lagarias y Odlyzko propusieron usar una variante de la formula de Riemann para calcular \(\pi(x)\). Para mejorar la convergencia de la integral de Riemann añadieron un factor \(F(s)\) al \(\log\zeta(s)\), este factor complica el otro miembro de la ecuación \(\Pi(x)\). De todos modos obtuvieron un método que teóricamente calcula \(\pi(x)\) en tiempo \(O(x^{3/5+\varepsilon})\) usando \(O(x^\epsilon)\) espacio, o en una segunda version en tiempo \(O(x^{1/2+\varepsilon})\) y usando \(O(x^{1/4+\varepsilon})\) espacio.
Avances del método combinatorio y los ordenadores.
En el cuadro podemos ver como se han ido sucediendo los cálculos. Hasta el \(\pi(10^{23})\) diversos autores han ido implementando versiones del método de Meissel-Lehmer con el que se han ido mejorando los resultados previos. Estos avances son en parte debidos a las mejoras en la potencia de los ordenadores, pero también a mejores implementaciones. En particular Gourdon y sus colaboradores consiguieron distribuir el cálculo entre los ordenadores de muchos colaboradores voluntarios distribuidos en la red. Esto implica una implementación en paralelo.
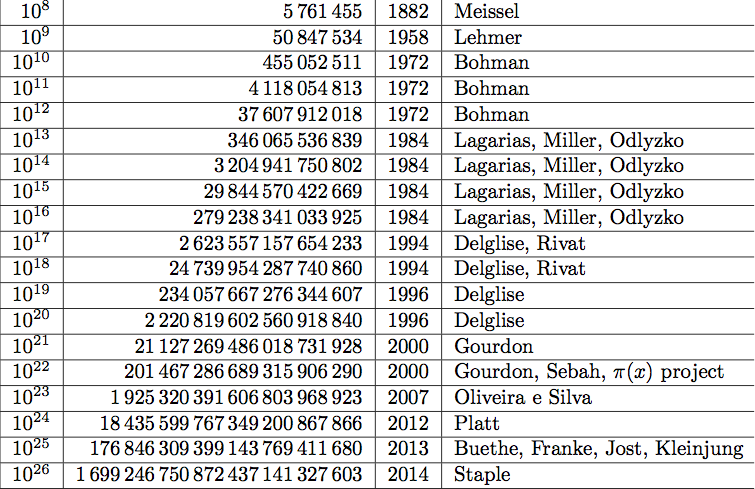Valores de pi(x) y primer cálculo correcto
Dada la frecuencia de errores en los cálculos de \(\pi(x)\) actualmente se procede de la siguiente forma: se calcula el valor deseado \(\pi(x)\) a continuación con un \(d\) pequeño se calcula \(\pi(x+d)\). La diferencia \(\pi(x+d)-\pi(x)\) tiene que coincidir con el número de primos en el intervalo \((x,x+d]\). En el caso del proyecto \(\pi(x)\) de Gourdon, calcularon el valor de \(\pi(10^{23})\), pero el chequeo probó que había un error en una unidad. Por esto el valor que figura en la tabla es el calculado posteriormente por Oliveira e Silva.
Primer éxito del método analítico.
En 2010 aparece el trabajo del equipo formado por Buethe, Franke, Jost y Kleinjung. Implementaron el método de Lagarias y Odlyzko con adecuadas modificaciones para obtener los valores
$$\pi(10^{23})=\mskip8.5mu
1\,925\,320\,391\,606\,803\,968\,923\quad
\pi(10^{24})=18\,435\,599\,767\,349\,200\,867\,866 $$
pero sus cálculos estaban obtenidos admitiendo cotas para los errores que dependían de la hipótesis de Riemann.
Dos años después en marzo de 2012 David J. Platt de la Universidad de Bristol consiguuió calcular rigurosamente, sin hacer ninguna hipótesis, los dos valores anteriores.
El cálculo de David J. Platt requirió calcular los \(69\,778\,732\,700\) ceros \(\frac12+i\gamma\) de la función \(\zeta(s)\) tales que \(0<\gamma<20\,950\,046\,000\), con 25 cifras decimales. El cálculo consumió \(63\,000\) horas de CPU, (2625 dias).
Cuando leí la hazaña de Platt, no me lo podía creer. No me podía imaginar que fuera posible calcular esa cantidad de ceros. Si el cálculo de cada cero hubiera tardado un segundo se habrían tardado \(807\,624\) años.
Segunda versión del método analítico.
En marzo de este año (2017) ha aparecido el trabajo
Franke, J, Kleinjung, T., Büthe, J., Jost, A., A Practical analytic Method for Calculating \(\pi(x)\)}, Math. Comp. 86 (2017) 2889-2909.
En él presentan un método que usa una fórmula explícita del tipo de la de Riemann, para calcular \(\pi(x)\). El método tiene dos versiones, una admitiendo la Hipótesis de Riemann y otra sin usarla que requiere más cálculo. Con este método ligeramente modificado es con el que han obtenido el valor de \(\pi(10^{25})\). La novedad es que este nuevo método es realmente práctico para calcular \(\pi(x)\). (Para un valor razonable de \(x\) algo menor que \(10^{25})\).
Pero cuando creíamos que esta era la última palabra y que el método analítico había ganado al fin nos encontramos con:
La última versión del método combinatorio.
En una tesis para el grado de master en la Universidad Dalhousie en Canada Douglas B. Staple ha mejorado el método de Meissel-Lehmer reduciendo el uso de memoria en un factor \(\log x\) y haciendo modificaciones sustanciales en el uso de la memoria en paralelo en el cálculo distribuido entre varios núcleos. El método resultante usa un espacio \(O(x^{1/3}\log^2 x)\) y un tiempo \(O(x^{2/3}/\log^2x)\). Con él se ha calculado (con comprobaciones) el valor
$$\pi(10^{26})=1\,699\,246\,750\,872\,437\,141\,327\,603$$
Los detalles están muy bien explicados en la tesis.
D. B. Staple, The Combinatorial Algorithm for computing $latex\pi(x)$},
Submitted in partial fulfillment of the requirements for the degree of Master of Science,
Dalhousie University, Halifax, Nova Scotia, (2015).
\(\pi(x)\) y la hipótesis de Riemann.
¿Por qué tanto interés en calcular \(\pi(x)\)? Naturalmente el principal motivo es que es difícil. Los alpinistas suben a las montañas, pero lo más que hacen es repetir la hazaña del primero que lo hizo. Aquí tenemos el aliciente de que la montaña es infinita y siempre podemos llegar más lejos.
Ahora en serio. La hipótesis de Riemann es equivalente a la cota
$$\bigl|\pi(x)-\mathrm{Li}(x)\bigr|<\frac{1}{8\pi}\sqrt{x}\;\log x,\qquad x\ge2657.$$
Büthe ha probado que si los ceros \(\rho\) de la función \(\zeta(s)\) con \(0<\Im(\rho)<T\) tienen parte real \(\frac12\) (es decir, si la hipótesis de Riemann es válida hasta la altura \(T\)), entonces la desigualdad anterior se cumple para los \(x\ge2657\) y tales que \(4.92\sqrt{x/\log x}\le T\). Puesto que hemos calculado los \(2\cdot 10^{13}\) primeros ceros, comprobando que todos están en la línea crítica, podemos tomar \(T=4\times 10^{12}\). Esto implica que sabemos que la desigualdad anterior para \(\pi (x)\) es válida para \(x\le 10^{25}\).
Por tanto los valores calculados de \(\pi(10^{26})\) están justo en el límite. ¿Podrían demostrar que la hipótesis de Riemann no es cierta? Por ahora no
$$155\,891\,678\,120.79=\bigl|\pi(10^{26})-\mathrm{Li}(10^{26})\bigr|<
\frac{1}{8\pi}\sqrt{10^{26}}\;\log 10^{26}=
23\,820\,406\,963\,581.40$$
La aproximación de Riemann.
El logaritmo integral \(\mathrm{Li}(x)\) es la aproximación que Gauss imaginó. Riemann fue capaz de encontrar un razonamiento que lleva de \(\pi(x)\) al logaritmo integral. Pero su razonamiento le lleva a otra aproximación mejor.
$$\pi(x)\sim R(x)=\mathrm{Li}(x)-\frac12\mathrm{Li}(x^{1/2})-\frac13\mathrm{Li}(x^{1/3})-\frac15\mathrm{Li}(x^{1/5})+\frac16\mathrm{Li}(x^{1/6})-\cdots$$
Es difícil precisar en qué sentido esta aproximación es mejor que \(\mathrm{Li}(x)\). Se sabe que para algunos valores de \(x\) tendremos \(|\pi(x)-\mathrm{Li}(x)|\le |\pi(x)-R(x)|\). Sin embargo esto parece que no es lo normal.
No me resisto a comparar los valores calculados con la aproximación de Riemann \(R(x)\). Los cambios frecuentes de signo de la diferencia \(\pi (x)-R(x)\) implican que es difícil mejorar esta aproximación con una función regular.
Escribimos en azul los dígitos de \(\pi(x)\) que coinciden con los de \(R(x)\).
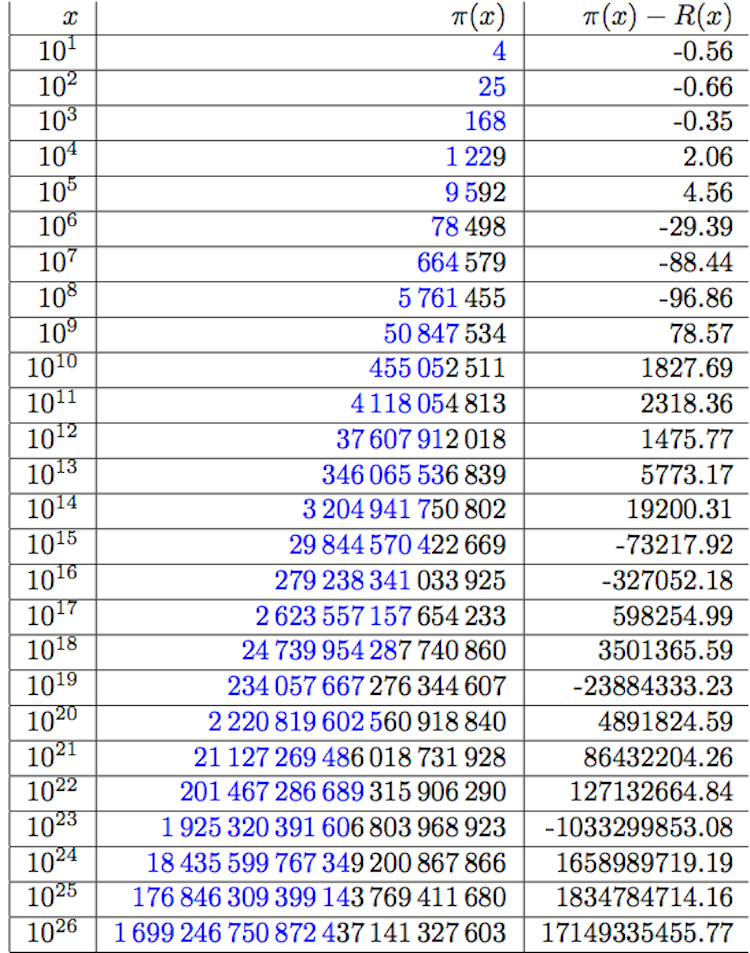Comparación \(\pi(x)\) con la función de Riemann \(R(x)\).
Dejar una contestacion