Solución: Triángulos

Publicamos la solución al divertimento Triángulos. Alberto Castaño, Rafael Jiménez y Javier Linares han propuesto soluciones al problema; también nos han hecho llegar una solución desde el blog La Tierra de las Matemáticas. ¡Gracias a todos por vuestras respuestas!

Divertimento:

Si el triángulo \(ABC\) de lados \(a\), \(b\) y \(c\) es isósceles, siendo \(a=b\), y denotamos por \(m_a\) y \(m_b\) las respectivas medianas sobre \(a\) y \(b\), entonces es sabido que \(m_a=m_b\), y por tanto, $$a+m_a=b+m_b.$$

El recíproco de este resultado no es cierto. Proponemos como primer ejercicio de este divertimento comprobar que el triángulo de lados $$a=16, b=8, c=\sqrt{114} $$ cumple la desigualdad anterior, y evidentemente no es isósceles. Pero sí es cierto que un triángulo es isósceles si y sólo si $$a+\frac{2}{3} m_a = b+\frac{2}{3} m_b.$$ Evidentemente, si el triángulo es isósceles, cumple esta igualdad; por tanto, proponemos como segundo ejercicio de este divertimento el siguiente: sea \(G\) el baricentro del triángulo \(ABC\). Si se verifica $$AB+GC=AC+GB,$$ entonces el triángulo es isósceles.

Solución:

Para la primera parte del problema utilizaremos el Teorema de la Mediana, que relaciona las longitud de una mediana con la longitud de los lados del triángulo:

$$m_a^2 =\frac{1}{2}\Big(b^2+c^2-\frac{a^2}{2} \Big).$$

Si \(a=16, b=8\) y \(c=\sqrt{114} \), se obtiene que \(m_a=5\). Con la identidad correspondiente para \(m_b\), se obtiene que \(m_b=13\). Por tanto, \(a+m_a=b+m_b=21\).

Para la segunda parte del problema se utilizará además la Fórmula de Herón, según la cual el área de un triángulo de lados \(a,b,c\) es

$$A=\sqrt{p(p-a)(p-b)(p-c)},$$

donde \(p=(a+b+c)/2\) es el semiperímetro del triángulo.

Denotemos \(A’, B’\) y \(C’\) a los puntos medios de los lados \(BC, AC\) y \(AB\) respectivamente, y \(m=AB’\), \(n=B’G\), \(m’=AC’\), \(n’=C’G\).

 

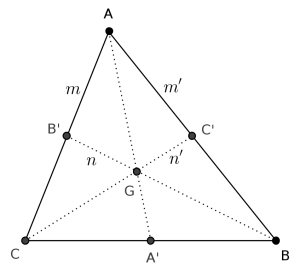
Según el Teorema de la Mediana,

$$ (3n)^2=\frac{1}{2}\Big( (2m’)^2+a^2 – \frac{1}{4}(2m)^2\Big), $$

de donde

$$9n^2=2(m’)^2+\frac{1}{2}a^2-m^2.$$

Análogamente, de la igualdad

$$ (3n’)^2=\frac{1}{2}\Big( (2m)^2+a^2 – \frac{1}{4}(2m’)^2\Big), $$

se tiene que

$$9(n’)^2=2m^2+\frac{1}{2}a^2-(m’)^2.$$

Restando miembro a miembro se obtiene la siguiente identidad:

\begin{equation}(1) \qquad 3(n^2-(n’)^2) = (m’)^2-m^2.\end{equation}

La condición $$a+\frac{2}{3} m_a = b+\frac{2}{3} m_b$$ es equivalente a $$2m’+2n’=2m+2n,$$ es decir, $$m’+n’=m+n,$$ de donde los triángulos \(AB’G\) y \(AC’G\) tienen el mismo perímetro. Además, estos triángulos tienen la misma área, porque tiene una base común, \(AG\), y las alturas de ambos triángulos sobre ella forman con la recta \(B’C’\) dos triángulos iguales. Denotemos ahora $$p=\frac{m+n+AG}{2}=\frac{m’+n’+AG}{2}.$$ Mediante la Fórmula de Herón se obtiene que $$(p-m)(p-n)=(p-m’)(p-n’),$$ que junto con la expresión anterior para el perímetro resulta $$m-m’=n-n’.$$

Si \(m-m’=n-n’=0\), el triángulo es isósceles. Por otra parte, si \(m-m’=n-n’\neq 0\), de la igualdad (1) se tiene que \(-3(n+n’)=(m+m’)\), lo que es absurdo porque un miembro es negativo y el otro positivo.