En todos los mundos posibles p = t.

Cantor creó la teoría de conjuntos. Para los matemáticos ha sido un paraíso. Un paraíso porque con los conjuntos es posible construir un modelo de todo lo consistente. Todo lo consistente existe y la existencia no es más que la consistencia. Pero junto a estos resultados tan satisfactorios, Cantor se encontró con el problema del continuo. ¿Hay un cardinal intermedio entre el de los números naturales \(\aleph_0\) y el de los números reales \(\frak c\)?

Ya sabemos que la cuestión es indecidible. Es la pena que acompaña al paraíso, hay muchos mundos posibles y tenemos que convivir con ellos. Hay dos tipos de mundos posibles:

1. No hay nada intermedio y por tanto \(\aleph_1\), el siguiente cardinal a \(\aleph_0\), coincide con \(\frak c\).
2. \(\aleph_1<\frak c\).

Dicho en los más coloquiales términos de la copa llena o medio vacía: tan válido es pensar que \(\aleph_1\) llena al cardinal de los números reales \(\frak c\) como que lo deja medio vacío.

La primera posibilidad es la más simple. Simplex sigillum veri (la simplicidad es el sello de la verdad) dice el antiguo adagio. Pero eso es no entender la situación, si hay dos mundos hay que explorar los dos. Y es el segundo el que nos ofrece más riqueza. Y es que en ese segundo mundo hay muchas preguntas que no sabemos responder. A una que propuso Fritz Rothberger (1902-2000) en 1948 no se le ha dado respuesta hasta hace muy poco. Rothberger definió dos cardinales entre el primer no numerable y el continuo \(\aleph_1\le \frak p\le\frak t\le \frak c\). Todo el mundo esperaba que existieran modelos de ZFC en los que \(\frak p<\frak t\); pero en 2016 se ha demostrado que \(\frak p=\frak t\) es un teorema de ZFC. Y la prueba sigue de un avance espectacular en la Teoría de Modelos obra de Maryanthe Malliaris y Saharon Shelah.

Cardinales intermedios.

Hay muchos cardinales \(\frak m\) que podemos definir y de los que podemos demostrar que

$$\aleph_1\le\frak m\le \frak c.$$

Por ejemplo: sea \(\frak m\) el menor cardinal de una familia \((N_i)\) de conjuntos de medida nula en \([0,1]\) tales que \(\bigcup_i N_i\) no tenga medida nula.

Sabemos que \(\aleph_1\le\frak m\) en caso contrario la familia \((N_i)\) es finita o numerable y su unión es de medida nula. Sabemos que \(\frak m\le \frak c\) pues basta tomar la familia \(N_x=\{x\}\) para \(x\in[0,1]\). Esta familia tiene cardinal \(\frak c\), está formado por conjuntos de medida nula y su unión es \([0,1]\) que no tiene medida nula.

El continuo, el cardinal de \([0,1]\), se puede ver también como el cardinal de los subconjuntos \(A\subset\mathbf{N}\) de los números naturales. Para construir un cardinal intermedio \(\aleph_1\le\frak s\le \frak c\) basta considerar propiedades \(\mathcal P\) de familias de subconjuntos de \(\mathbf{N}\) que se cumplen para cualquier familia numerable y fallan para alguna del tamaño del continuo. Para una tal propiedad definimos el cardinal \(\frak s\) como el menor de alguna familia que no tenga la propiedad \(\mathcal P\). Usaremos esta idea para construir los dos cardinales intermedios notables \(\frak p\le \frak t\) de Rothberger.

Cardinales p y t.

Podemos definir muchos cardinales intermedios entre \(\aleph_1\) y \(\frak c\), para algunos su definición depende de conceptos de topología o teoría de la medida como el que hemos definido antes \(\frak m\). Los que nos interesan ahora tienen una definición combinatoria (aunque combinatoria infinita).

En primer lugar debemos familiarizarnos con el conjunto de las partes \({\mathcal P}(\mathbf{N})\) de \(\mathbf{N}\). Algunos de sus elementos serían los números impares \(A=\{2n-1,\colon n\in\mathbf{N}\}\), los primos \(P=\{p\colon p \text{ primo }\}\), los cuadrados \(Q=\{n^2\colon n\in\mathbf{N}\}\). El conjunto \({\mathcal P}(\mathbf{N})\) es enorme (su cardinal es precisamente \(\frak c\)) y no acabaríamos nunca de dar ejemplos.

Ahora consideraremos dos elementos \(A\), \(B\) de \({\mathcal P}(\mathbf{N})\) como equivalentes, \(A\sim B\), si tienen los mismos elementos salvo un número finito de excepciones, por ejemplo los números primos \(P\) sería equivalente al conjunto \(P_{1000}\) de los números primos mayores que 1000. Designaremos por \([A]\) la clase de todos los elementos de \({\mathcal P}(\mathbf{N})\) equivalentes a uno dado \(A\).

Una clase importante es la clase del vacío \([\emptyset]\), que está formada por todos los conjuntos finitos de \(\mathbf{N}\). Un elemento \(B\) de cualquier otra clase \([A]\) ha de ser infinito.

Hay una relación de orden que podemos definir entre clases: diremos que \([A]\le [B]\) si la diferencia \(A\setminus B\) es un conjunto finito. Esto es equivalente a decir que existe un número \(n_0\) tal que todos los elementos de \(A\) mayores que \(n_0\) están contenidos en \(B\). Esto no depende de los representantes \(A\) y \(B\) de las clases \([A]\) y \([B]\).

Se tiene que \([\emptyset]\le [A]\) para toda clase \([A]\).

Podemos definir también la intersección de dos clases. Por definición \([A]\cap [B]\)  es \([A\cap B]\). Es un pequeño ejercicio ver que la definición no depende de los representantes \(A\) y \(B\).

Con estos elementos ya podemos definir los dos cardinales \(\frak p\) y \(\frak t\).

\(\frak p\) es el mínimo cardinal de una familia \(\mathcal F\) de clases \([A]\) con dos propiedades:

1. Para todo conjunto finito de clases \([A_1]\), \([A_2]\), … , \([A_n]\) en \(\mathcal F\) la intersección \([A_1\cap A_2\cap \cdots\cap A_n]\ne [\emptyset]\).
2. Si \([M]\) verifica \([M]\le [A]\) para todo \([A]\in \mathcal F\), entonces \([M]= [\emptyset]\).

Notar que la intersección de una conjunto finito de clases está bien definida pero no podemos definir la intersección de infinitas clases.

Las dos condiciones impuestas a \(\mathcal F\) son como opuestas. Es difícil dar un ejemplo de una familia \(\mathcal F\) con las dos propiedades. Hausdorff en 1936 probó que una familia numerable que cumpla la primera condición, no verifica la segunda. Por tanto que \(\frak p\ge \aleph_1\). Por otro lado, es obvio que \(\frak p\le \frak c\)  pues el cardinal de \(\mathcal P(\mathbf{N})\) es \(\frak c\).

El otro cardinal que nos interesa \(\frak t\) se define de una manera análoga: es el menor cardinal de una familia \(\mathcal F\) de clases \([A]\) con tres propiedades:

1. \(\mathcal F\) no contiene la clase \([\emptyset]\).
2. \(\mathcal F\) es totalmente ordenado, es decir, si \([A]\) y \([B]\) son dos elementos de \(\mathcal F\), o bien \([A]\le[B]\) ó \([B]\le[A]\).
3. Si \([M]\) verifica \([M]\le [A]\) para todo \([A]\in \mathcal F\), entonces \([M]= [\emptyset]\).

Una tal familia se dice que es una torre y \(\frak t\) es el menor cardinal de una torre.

Es muy fácil ver que \(\frak p\le \frak t\) porque cualquier torre por definición cumple las condiciones de las familias que definen \(\frak p\).

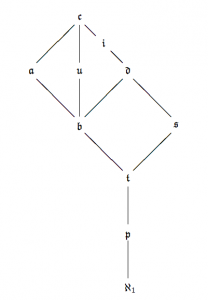
Las definiciones de estos dos cardinales se deben a F. Rothberger (1939, 1948), un matemático austríaco que tuvo que emigrar a Canadá. Y la cuestión de si \(\frak p <\frak t\) ya surgió en los trabajos de Rothberger. Los matemáticos han dedicado mucha atención a esta cuestión y a la relación de estos cardinales con otros. En 1984 van Douwen (ver [7]) enfocó la atención en seis cardinales \(\frak b\), \(\frak p\), \(\frak t\), \(\frak d\), \(\frak a\) y \(\frak s\), y planteó como el problema pendiente más importante el de saber si \(\frak p <\frak t\).

En la figura tomada de Vaughan [8] podemos ver las relaciones entre los cardinales en 1990. Entre los 8 cardinales que figuran en el diagrama hay \(64-8\) cuestiones de la forma «es \(\frak k<\frak l\)». Según Vaughan, en 1990 quedaban pendientes solo 5 de ellas, dos si solo contamos los seis cardinales de van Douwen: \(\frak p<\frak t\) y \(\frak d<\frak a\). En 1990 Vaughan escribió: «Pensamos que la más importante de todas es: ¿es \(\frak p<\frak t\) consistente?». En 2004, en un articulo publicado en Acta Math, S. Shelah demostró que \(\frak d<\frak a\) es consistente.

La demostración de p = t.

Después de los trabajos de Rothberger en 1948 se han obtenido muchos resultados sobre los dos cardinales \(\frak p\) y \(\frak t\). Dado el tiempo transcurrido todo el mundo pensaba que \(\frak p<\frak t\) sería consistente con la teoría. Sin embargo Maryanthe Malliaris y Saharon Shelah en [5] acaban de demostrar que \(\frak p=\frak t\) es un teorema de ZFC, es decir han demostrado que  \(\frak p=\frak t\) usando solo los axiomas usuales de la Teoría de Conjuntos. Como consecuencia, los dos cardinales coinciden en cualquier modelo de la Teoría de Conjuntos.

El resultado \(\frak p=\frak t\) es consecuencia de otros resultados mucho más potentes obtenidos por  Malliaris y Shelah en Teoría de Modelos. Concretamente sobre la complejidad de las teorías de primer orden. De hecho, Malliaris y Shelah han resuelto un problema planteado hace unos 40 años en Teoría de Modelos sobre el orden de Keisler; este orden es una medida de la complejidad de las teorías de primer orden. No vamos a entrar en explicar esta parte de su trabajo. Sí debemos decir que puede que sea la más importante por sus consecuencias. Remitimos al lector interesado a la referencia Moore [4], Malliaris y Shelah [6], o finalmente su trabajo completo [5].

Reto de Gowers.

El hecho de que \(\frak p=\frak t\) sea consecuencia indirecta de un resultado sobre complejidad en Teoría de Modelos puede producir cierta insatisfacción. Por ejemplo, el medalla Fields T. Gowers ha sugerido que habría que buscar una prueba directa: partiendo de una familia de cardinal \(\frak p\) verificando las condiciones de la definición de \(\frak p\), la demostración debería ser capaz de construir una torre con las tres propiedades que definen \(\frak t\) y que tenga el cardinal de \(\frak p\).

De hecho Rothberger en 1948 demostró que si \(\frak p=\aleph_1\), el menor valor que puede tomar, entonces \(\frak t\) es también igual a \(\aleph_1\), y por tanto en ese caso \(\frak p=\frak t =\aleph_1\).

De todos modos antes de intentar el reto de Gowers, debemos mirar un poco la entrada de su blog sobre el tema [3] y los comentarios que se sucedieron, no parece un reto fácil.

Los autores.

Saharon Shelah puede ser uno de los autores más prolíficos. Actualmente una búsqueda en MathSciNet da cuenta de 1025 artículos publicados bajo su nombre. Nació en 1945 en Jerusalén, ahora es profesor en la Universidad de Jerusalén y en Rutgers, New Jersey. Sus trabajos se centran en Lógica Matemática, Teoría de Modelos y Teoría de Conjuntos. Entre sus logros está la introducción de la técnica del proper forcing y la solución del problema de Morley, en la que demuestró una dicotomía con respecto al cardinal del conjunto de modelos de una teoría de primer orden.

Maryanthe Malliaris es profesora asociada en la Universidad de Chicago, es especialista en Teoría de Modelos. Se graduó en 2001 en Harvard y realizó su Ph. D. en la Universidad de California en Berkeley.

 

 

Para saber más.

[1] Mathematicians Measure Infinities and Find They’re Equal. Entrada de Quanta Magazine.

[2] John Baez blog: MATHEMATICIANS MAKE IMPORTANT DISCOVERY But Details Don’t Matter. Una crítica a la entrada en Quanta.

[3] Gowers blog:Two infinities that are surprisingly equal.

[4] Una explicación no demasiado técnica sobre la parte del trabajo de Malliaris y Shelah relativa a la Teoría de Modelos:
J. T. Moore, Model Theory and the cardinal numbers \(\frak p\) and \(\frak t\). Proc. Nat. Acad. Sciences (commentary).

[5] El trabajo con la demostración completa:
M. Malliaris, S. Shelah, Cofinality spectrum theorems in Model Theory, Set Theory, and General Topology, J. Amer. Math. Soc. 29 (2016) 237-297.

[6] Una versión para un público mas general:
M. Malliaris, S. Shelah, General Topology meets model theory, on \(\frak p\) and \(\frak t\), Proc. Nat. Acad. Sci. 110 (2013), 13300-13305.

[7] E. van Douwen, The Integers and Topology, en Handbook of Set-Theoretic Topology, eds. K. Kunen, J. Vaughan, North-Holland, Amsterdam, 1984 p. 111-167.

[8] J. Vaughan, Small uncountable cardinals and topology, en
Open problems in topology, eds. J. van Mill, G. M. Reed, North-Holland, Amsterdam, 1990 p. 195-218.