Solución: El problema de la mesa de diálogo para Cataluña

Publicamos la solución al divertimento El problema de la mesa de diálogo para Cataluña. Alberto Castaño y Sebastià Xambó han sido capaces de encontrar un encaje en la mesa para las ocho personas. ¡Gracias por vuestras respuestas!

Divertimento:

Ocho personas desean sentarse en los vértices de una mesa octogonal, aunque algunos de ellos no desean hacerlo junto a algunos de los demás. En particular, A no quiere sentarse junto a B ni D; B no quiere sentarse junto a A, E, F ni H; C no quiere sentarse junto a D ni E; D no quiere sentarse junto a A, C ni G; E no quiere sentarse junto a B, C ni F; F no quiere sentarse junto a B, E ni H; G no quiere sentarse junto a D ni H; y, por último, H no quiere sentarse junto a B, F ni G. Deducir si es posible conseguir que los 8 se sienten en la mesa respetando todas las incompatibilidades anteriores.

 Solución:

El número total de posibilidades que tienen 8 personas para sentarse en una mesa octogonal es (8-1)! = 5040. Representando el problema mediante un grafo vamos a evitar escribirlas todas y descartar las configuraciones que no son válidas.

Construmos un grafo de forma que cada persona será un vértice, y dos vértices estarán unidos por una arista en caso de que las personas que representan no acepten sentarse juntos:

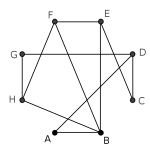
En el grafo complementario, dos vértices están unidos por una arista si y sólo si no están unidos en el original. En este caso, el grafo complementario es

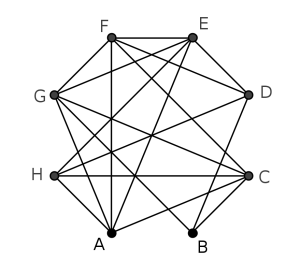
Este grafo tiene representadas las compatibilidades en la mesa. Este grafo tiene un ciclo Hamiltoniano (camino cerrado que visita todos los vértices una única vez) que nos proporciona (al menos) una solución. Así, una posible configuración de la mesa sería, por ejemplo, AGBCFDEH.

Además, Alberto Castaño nos apunta que la condición de Rahman-Kaykobad se aplica en este grafo, y es suficiente para garantizar la existencia de un ciclo Hamiltoniano. Por otra parte, Sebastià Xambó nos ha hecho llegar 38 soluciones posibles al problema:

ACBDFGEH

ACBDHEGF

ACBGEHDF

ACBGFDEH

ACBGFDHE

ACFDBGEH

ACFGBDEH

ACFGBDHE

ACHEDBGF

ACHEGBDF

AEDBGFCH

AEDFGBCH

AEDHCBGF

AEGBCFDH

AEGBCHDF

AEGBDFCH

AEGBDHCF

AEGFCBDH

AEGFDBCH

AEHCBDFG

AEHCFDBG

AEHCGBDF

AEHDBCFG

AEHDBCGF

AEHDBGCF

AEHDFCBG

AFCBDHEG

AFCBGEDH

AFCGBDEH

AFCHEDBG

AFDBCGEH

AFDBCHEG

AFDEGBCH

AFDEHCBG

AFGCBDEH

AFGEDBCH

AGBCFDEH

AGFCBDEH