El problema del corredor solitario

Hoy vamos a comentar la historia de un problema. Es una historia inacabada. Todavía desconocemos su solución. No es un problema imposible. Fue planteado hace 50 años. En cuanto lo vi enunciado me gustó y decidí dedicarle una entrada del blog. No sabía yo que terminaría en la cocina.

Un conjunto \(\{A_0, A_1,\dots. A_n\}\) de \(n+1\) corredores parten del mismo punto de una circunferencia de longitud \(1\). No se trata de una competición. Puede que ni siquiera vayan todos en el mismo sentido, pero sus velocidades \(v_0\), \(v_1\), …, \(v_n\) son constantes, todas diferentes.

¿Existe una constante \(\delta_n\) tal que no importa cual sea el conjunto de velocidades exista un momento \(t>0\) tal que en el tiempo \(t\) la distancia (medida a lo largo de la circunferencia) de \(A_0\) a cualquier otro corredor \(A_k\) sea mayor o igual a \(\delta_n\)?

Wills en 1968 respondió a esta pregunta, demostró que sí existe \(\delta_n\) y que además \(\frac{1}{2n}\le\delta_n\le \frac{1}{n+1}\). Conjeturó que para todo \(n\ge1\) se tiene \(\delta_n=\frac{1}{n+1}\).

Problema. ¿Hay algún tiempo \(t>0\) tal que el corredor \(A_0\) se encuentre aislado, es decir tal que la distancia (medida a lo largo de la circunferencia) de \(A_0\) con cualquier otro corredor sea \(\ge\frac{1}{n+1}\)?

La fracción \(\frac{1}{n+1}\) es solo una conjetura. En general podemos preguntar ¿cuánto vale \(\delta_n\)?

Vemos aquí (caso \(n=6\), con 7 corredores) que el corredor azul consigue en  algún momento que los otros corredores respeten dos séptimos de la circunferencia (en azul) para él solo.  Las velocidades en este caso son \(\{1,2,3,4,5,6,7\}\). Este es un caso extremo en cada ciclo solo hay un momento en que el corredor azul esté aislado,  en ese momento un corredor sale por un extremo de la zona azul, justo cuando otro entra por el otro extremo. Eso prueba que \(\delta_6=1/7\) no puede mejorarse.

Este no es el único conjunto de velocidades extremal. Estos conjuntos extremales de velocidades aumentan con \(n\). Cusick y Pomerance en [3] señalan esto como una de las dificultades para una prueba válida para todo \(n\).

 

Otras formulaciones del problema.

Imaginemos que un espectador está sentado viendo a los corredores. Si el espectador se mueve con el corredor \(A_0\) puede pensar que la velocidad de \(A_0\) es \(=0\) y que los demás se mueven con velocidades \(v_j-v_0\). Podemos identificar la circunferencia con \(\mathbf{R}/\mathbf{Z}\), o también con el intervalo \([0,1)\). Si un corredor va con velocidad \(v\) su posición en el tiempo \(t\) será \(\{tv\}\), donde \(\{x\}\) denota la parte fraccionaria del número real \(x\).

De este modo vemos que nuestro problema es equivalente a probar la siguiente conjetura:

Conjetura 1. Para cualquier colección \(v_1\), …, \(v_n\) de números reales no nulos, existe \(t>0\) tal que se tiene:
$$\{v_j t\}\in\bigl[\text{$\frac{1}{n+1}$},\text{$\frac{n}{n+1}$}\bigr],\quad\text{para } j=1, \dots, n.$$

Una consecuencia es que podemos suponer que todas las velocidades son positivas, ya que \(\{-v_jt\}\) está en el intervalo \([\frac{1}{n+1},\frac{n}{n+1}]\) si y solo si lo está \(\{v_jt\}\).

Otra formulación interesante lo convierte en un problema de recubrimiento. Para un \(n\) fijado sea $$B=\{x>0\colon \exists; k\in\mathbf{Z} \text{ tal que } |x-k|<\text{$\frac{1}{n+1}$}\}$$ Si \(x_j=\frac{1}{v_j}\), el corredor \(j\) estará cercano al origen, precisamente cuando \(t\in x_j B\). Así que existe un tiempo \(t\) en que el origen estará solitario si y solo si \(t\) no está en ninguno de los \(x_j B\). Es decir, si $$\bigcup_{j=1}^n x_j B\ne \mathbf{R}^+.$$

Esta formulación se usa para probar que \(\delta_n\ge\frac{1}{2n}\).

El caso \(n=1\) es trivial. Si \(v>0\) es la velocidad, existe un tiempo \(t>0\) tal que \(tv=\frac12\). Con lo que \(\{tv\}=\frac12\in [\frac12,\frac12]\).

Hay otra equivalencia que no es fácil de establecer. La conjetura 1 equivale a la conjetura 2 en que las velocidades son todas números naturales.

Conjetura 2. Para cualquier colección \(v_1\), …, \(v_n\) de números naturales, existe \(t>0\) tal que se tiene: $$\{v_j t\}\in\bigl[\text{$\frac{1}{n+1}$},\text{$\frac{n}{n+1}$}\bigr],\quad\text{para } j=1, \dots, n.$$

La equivalencia se suele atribuir a Wills, pero sus definiciones son ligeramente diferentes y lo que el prueba no es exactamente la equivalencia que decimos. Una prueba satisfactoria de la equivalencia (siguiendo las ideas de la prueba de Wills) puede verse en [4]. Necesita de una versión fuerte del teorema de Kronecker .

Avances del problema.

Solución de los primeros casos.

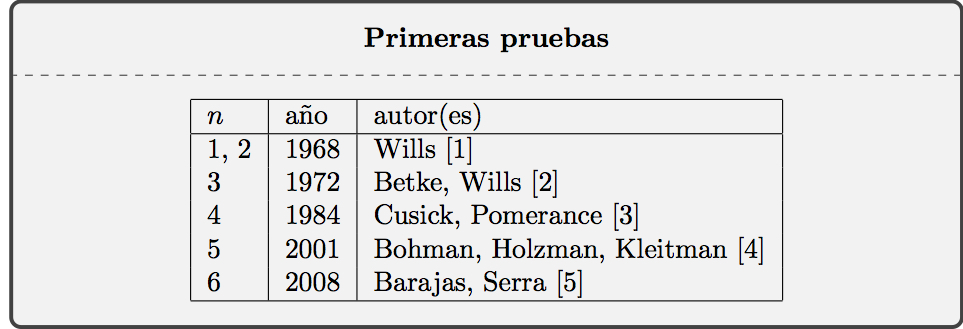
Hasta ahora se han probado los seis primeros casos de la conjetura para \(n=1\), \(2\), …, \(6\) (Como el número de corredores es \(n+1\), hay que tener cuidado, algunos prefieren hablar del número de corredores \(n+1\) que de \(n\).)

Vemos en la tabla los años y autores de las primeras pruebas de cada caso. Pero este cuadro no refleja bien el hecho de que la conjetura se ha considerado desde muchos puntos de vista y se han dado pruebas alternativas muy diferentes y en ocasiones mucho mas simples.

Aproximación diofántica.

El primero que consideró el problema fue Wills en 1968. Su motivación fue la aproximación diofántica. En esta teoría se considera frecuentemente la función \(\Vert x\Vert\). Wills estudió sistemáticamente cantidades como $$\kappa(n)=\sup_{v_j\in \mathbf{R}\setminus \mathbf{Q}}\ \sup_{t\in \mathbf{Z}}\ \min_{1\le j\le n}\Vert t v_j\Vert.$$ Probó que $$\kappa(n)=\inf_{v_j\in\mathbf{N}}\ \max_{0\le t\le 1}\ \min_{1\le j\le n}\Vert t v_j\Vert.$$ Podemos ver que la segunda expresión es nuestro \(\delta_n\).

Interpretación geométrica.

En 1973 Cusick [1] dio la segunda prueba del caso \(n=3\), es también la primera vez que se da la versión actual del problema. Para Cusick es un problema de obstrucción de la visión.

Dado un cuerpo convexo \(K\subset\mathbf{R}^n\) con interior no vacío y un número real positivo \(\alpha>0\) considera el conjunto obtenido situando copias homotéticas \(\alpha K\) de \(K\) formando el conjunto $$\Delta(K,\alpha):=\bigcup_{(m_1,m_2,\dots,m_n)\in\mathbf{Z}_+^n} (m_1+\text{$\frac12$},\dots, m_n+\text{$\frac12$})+\alpha K.$$ Formula entonces el problema siguiente:

Problema. Encontrar la constante \(\delta(K)\) ínfimo de los \(\alpha>0\) tal que cualquier semirrecta \(L(a_1,\dots,a_n):=\{(a_1,\dots,a_n)t\colon t>0\}\) donde los \(a_j\) son números reales positivos, corte al conjunto \(\Delta(K,\alpha)\).

Cusick relacionó este problema con el del corredor solitario, demostrando que cuando tomamos \(K=[-1/2,1/2]^n\) tenemos \(\delta(K)=1-2\delta_n\).

Puesto que las semirrectas \(L\) pueden ser consideradas como líneas de visión de un observador en el origen, Cusick llama a este tipo de problemas problemas de obstrucción de la visión.

La prueba que da del caso \(n=3\) descansa precisamente en esta interpretación del problema.

Todavía Cusick vuelve a dar otra prueba en el caso \(n=3\) en [8]. En este caso el razonamiento se basa en considerar las velocidades \(v_1\), \(v_2\), …, \(v_n\) como números naturales no divisibles por el mismo primo (sin perder generalidad). Entonces determina las velocidades extremales, es decir aquellos conjuntos de velocidades tales que no existe \(t\) verificando $$\{v_j t\}\in\bigl(\text{$\frac{1}{n+1}$},\text{$\frac{n}{n+1}$}\bigr),\quad\text{para } j=1, \dots, n.$$ (notar que el intervalo ahora es abierto. Puede esperarse que estos conjuntos sean en número finito y su determinación lleve a la prueba de la conjetura.

Este tipo de ideas son las que usaron en 1984 (12 años después) Cusick y Pomerance en [3] para probar el siguiente caso \(n=4\). El procedimiento aquí es mucho mas complicado y necesita acotaciones de sumas de exponenciales y un chequeo por ordenador.

Flujos en grafos.

Un giro importante del problema lo dan Bienia et al. en [9]. Relacionándolo con problemas clásicos de la teoría de grafos.

Sea \(G=(V,E)\) un grafo no dirigido, \(V\) es el conjunto de vértices y \(E\) el de aristas del grafo. Un flujo no nulo en \(G\) es dar una orientación a las aristas y un número natural a cada una de forma que en cada vértice el flujo entrante coincide con el saliente. Un puente es una arista tal que el grafo sin esa arista tiene mas componentes conexas que con ella. Una conjetura clásica de la teoría de grafos

Conjetura (Tutte, 1954). Un grafo sin puentes admite un flujo no nulo con valores en \(\{1,2,3,4\}\).

Seymour en 1981 demostró que cualquier grafo sin puentes admite un flujo, no nulo con valores en \(\{1,2,3,4,5\}\).

Lo que Bienia et al [9] prueban es el teorema
Teorema. Sea \(G\) un grafo no orientado, si \(G\) admite un flujo no nulo con a lo mas \(k\) valores distintos, entonces también admite un flujo no nulo con valores del conjunto \(\{1,\dots, k\}\).

Para \(k\ge5\) el teorema es consecuencia directa del teorema de Seymour ya que si el grafo admite un flujo no nulo entonces no tiene puentes. Pero cuando \(k\le 4\), Biennia et al usan los valores del flujo \(f_j\) como velocidades en el problema del corredor solitario, encuentran un tiempo \(t>0\) en que casi todos los productos \(t f_j\) están en el intervalo \([1/(k+1), k/(k+1)]\) y a partir de el construyen el flujo deseado.

Por tanto su teorema es consecuencia del resultado anterior de Cusick y Pomerance. Pero ellos lo prueban de nuevo, de una manera mucho mas simple.

En [9] varios autores consideran de nuevo los casos \(n=3\) y \(n=4\). El método es muy diferente. Luis Goddyn, uno de los autores, es el que da el nombre de corredor solitario al problema. La prueba del caso \(n=4\) es considerablemente mas simple que la de Cusick y Pomerance. Usan la estructura de grupo del conjunto de valores \(\{tv_j\}\) con la suma modulo \(1\).

La demostración del caso \(n=6\), el último que se conoce, se debe a dos matemáticos catalanes J. Barajas y O. Serra de la Politécnica de Cataluña. Su prueba usa también de la teoría de grafos. Ellos formulan la conjetura del corredor solitario en términos de lo que llaman el número cromático regular de un conjunto finito \(D\) de números naturales. La prueba es complicada y usa de manera importante el hecho de que \(7=6+1\) es primo.

Últimos avances.

En enero de este año Terry Tao colgó en arXiv el artículo [10]. En el hace dos contribuciones. La que considero mas trascendente es probar que existe un algoritmo que en tiempo finito decide la conjetura para todo \(n\le N\). El algoritmo no es practicable ya que el tiempo necesario para la decisión es \(O(N^{c N^2})\) para cierta constante \(c>0\).

Tao observa además que las pruebas dadas en los seis primeros casos no parecen admitir una extensión para todo \(n\).

El segundo resultado de Tao extiende el trabajo de otros autores. Por ejemplo podemos citar el trabajo de dos matemáticos catalanes [11]. Sabemos que \(\frac{1}{2n}\le \delta_n\le \frac{1}{n+1}\). El objetivo en este caso es tratar de mejorar la cota inferior. Para esto Perarnau y su profesor Oriol Serra estudian la correlación entre los tiempos que los corredores pasan cerca del origen.

Con estos métodos probabilisticos consiguen probar que $$\delta_n\ge\frac{1}{2n-2+o(1)}.$$ Esto mejora un resultado anterior de Chen que probaba \(\delta_n\ge\frac{1}{2n-1}\).

Perarnau y Oriol comentan que aunque parece modesto, hasta la fecha en que lo publicaron era el mejor resultado sobre la conjetura del corredor solitario válida para todo \(n\). Pues bien, Tao en [10] consigue mejorar este resultado mostrando, con todas las herramienta del análisis armónico y la combinatoria aditiva, que $$\delta_n\ge \frac{1}{2n}+\frac{c\log n}{n^2(\log\log n)^2}, \qquad n\ge n_0.$$ También esto sabe a poco. Nos queda un largo trecho hasta \(\frac{1}{n+1}\), o bien, quizás para \(n\) grande la conjetura no es cierta.

Guillem Perarnau es otro de los matemáticos españoles maltratado por su país. Formado en la Universitat Politècnica de Catalunya, lo tenemos aparcado en la Universidad de Birmingham. ¡Cómo lo podemos consentir…! Aparte de todo si visitáis su página web podréis ver que además de buen matemático es un buen cocinero.

Tao tiene una entrada en su blog sobre el problema.

Casi todos los principales trabajos sobre el tema tienen acceso libre en la red:

[1] T.W. Cusick, View-obstruction problems, Aequationes Math. 9 (1973) 165–170.

[2] U. Betke, J.M. Wills, Untere Schranken für zwei dophantische Approximations-Funktionen, Monatsh. Math. 76 (1972) 214-217.

[3] T.W. Cusick and C. Pomerance, View obstruction problems III, Journal of Number Theory 19 (1984) 131-139.

[4] T. Bohman, R. Holzman, D. Kleitman, Six lonely runners, Electron. J. Combin. 8 (2001), no. 2, Research Paper 3, 49 pp.

[5] J. Barajas, O. Serra, The lonely runner with seven runners, Electron. J. Combin. 15 (2008), R48, 18 pp.

[6] T.W. Cusick, View-obstruction problems, Aequationes Math. 9 (1973) 165-170.

[7] J. Renault, View-obstruction: a shorter proof for 6 lonely runners. Discrete Math. 287 (2004) 93-101.

[8] T. W. Cusick, View-Obstruction Problems. II, Proc. Amer. Math. Soc. 84, (1982) 25-28.

[9] W. Bienia, L. Goddyn, P. Gvozdjak, A. Sebö, M. Tarsi, Flows, view obstructions, and the lonely runner, J. Combin. Theory Ser. B, 72 (1998) 1-9.

[10] T. Tao, Some remarks on the lonely runner conjecture, por aparecer en Contrib. Disc. Math., arXiv:1701.02048v4.

[11] G. Perarnau, O. Serra, Correlation among runners and some results on the lonely runner conjecture, Electronic J. Combin. 23 (2016) no. 1, Paper 1.50, 22pp.