¿Cuántas líneas podemos encontrar formando un mismo ángulo tomadas de dos en dos? En el plano las tres diagonales de un hexágono regular forman ángulo de 60 grados.
¿Podemos encontrar cuatro líneas en el plano formando un mismo ángulo? Como solo pensamos en los ángulos podemos imaginar que las rectas pasan todas por el origen. Después de un pequeño razonamiento vemos que en el plano no es posible encontrar cuatro rectas equiangulares.
En el espacio tenemos mas libertad. Dos cualesquiera de las seis diagonales de un icosaedro forman un ángulo de unos 63 grados. Este es el número máximo de líneas equiangulares en \(\mathbf{R}^3\).
En general sea \(N(n)\) el número máximo de líneas en \(\mathbf{R}^n\) todas formando el mismo ángulo.
Vemos que \(N(2)=3\), \(N(3)=6\), … El problema de determinar \(N(n)\) fue considerado por primeravez hace 70 años por Haantjes [1]. Al principio el progreso fue lento. En 1966 van Lint y Seidel probaron que \(N(4)=6,\) \(N(5)=10,\) \(N(6)=16\) y \(N(7)\ge28\). En su trabajo van Lint y Seidel plantean el problema general.
Un conjunto de líneas es equiangular si el ángulo que forman dos cualesquiera de ellas es siempre el mismo.
Problema: ¿Cual es el cardinal máximo \(N(n)\) de un conjunto equiangular de líneas en \(\mathbf{R}^n\)?
Un problema matemático es siempre una ocasión de afinar las herramientas matemáticas. Este es un gran ejemplo.
El álgebra lineal.
El algebra lineal permite dar una cota superior de \(N(n)\).
Teorema (Gerzon).
Para todo \(n\ge2\) se tiene \(N(n)\le {n+1\choose 2}\).
Sea \(E\) un conjunto de líneas equiangular en \(\mathbf{R}^n\). Sean \(\mathbf{v_1}\), \(\mathbf{v_2}\), …, \(\mathbf{v_N}\) vectores unitarios en la dirección de las líneas, escogemos uno de los dos vectores unitarios que definen cada dirección. Decir que el conjunto es equiangular significa que los productos escalares son todos iguales en valor absoluto \(|\langle \mathbf{v_j},\mathbf{v_k}\rangle|=\cos\alpha\) si \(0<\alpha\le\pi/2\) denota el ángulo que forman las líneas del conjunto \(E\).
Si consideramos los vectores como vectores columna (matrices de dimensión \(n\times1\)), entonces los productos \(\mathbf{v_j}\times \mathbf{v_j}^T\) son matrices \(n\times n\). Es fácil probar que las \(N\) matrices \(\mathbf{v_j}\times \mathbf{v_j}^T\) son linealmente independientes y simétricas. Luego \(N\) es menor que la dimensión del espacio de las matrices simétricas de dimensión \(n\times n\). De manera que \(N\le {n+1\choose 2}\).
Una demostración completa, que es muy simple, podemos encontrarla en el delicioso libro de J. Matousek, Thirty-three miniatures. Mathematical and algorithmic applications of linear algebra.
Gerzon no publicó su teorema. Se publicó por primera vez en el trabajo de P. W. H. Lemmens y J. J. Seidel [4], en 1973, ellos probaron el teorema y lo atribuyeron a Gerzon.
El teorema de Gerzon da el valor exactamente en las dimensiones \(2\) y \(3\). En dimensión 7, nos dice que \(N(7)\le 28\). Es fácil ver que los vectores que se obtienen permutando las coordenadas de \((1,1,1,1,1,1,-3,-3)\) son 28 vectores cuyos productos escalares son iguales a \(8\) o \(-8\). Están contenidos en \(\mathbf{R}^8\), pero puesto que la suma de las coordenadas es siempre \(0\), están contenidos en un espacio de dimensión \(7\). Esto prueba que \(N(7)=28\). También en dimensión 23 la cota de Gerzón se alcanza y \(N(23)=276\). Pero \(n=2\), \(3\), \(7\) y \(23\) parecen ser los únicos casos de igualdad.
La sucesión A002853.
La sucesión \(N(n)\) es A002853 en OEIS la enciclopedia de sucesiones de Sloane. Es difícil determinar los valores exactos y el estado actual del conocimiento lo podemos resumir en la tabla siguiente extraída de [6]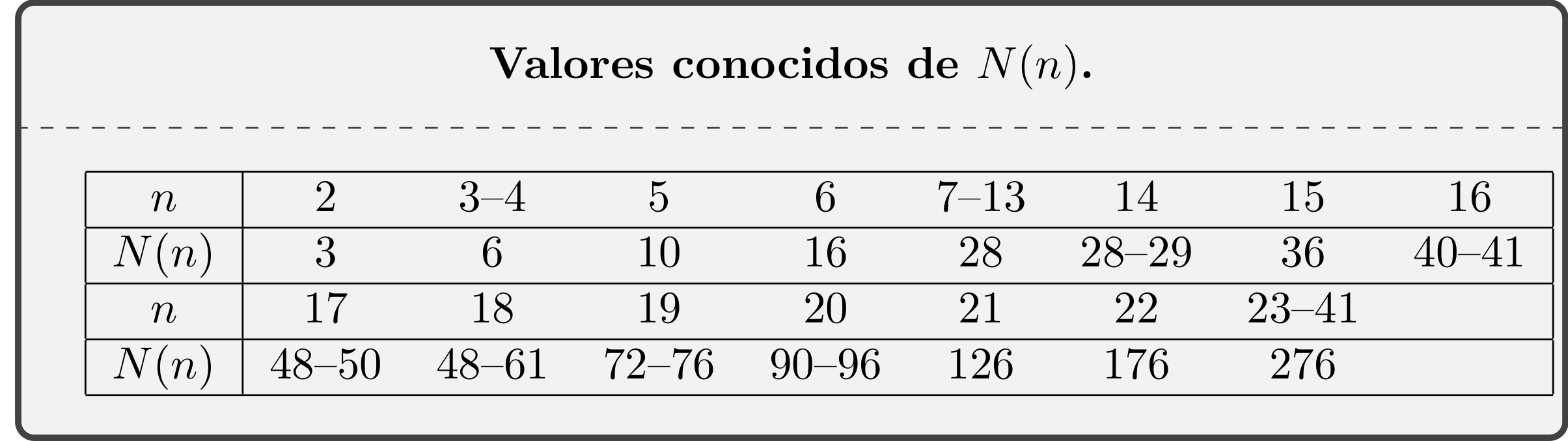
Aunque este es un terreno que se mueve cada día. Por ejemplo en [8] Wei-Hsuan Yu prueba, aparentemente de forma correcta, que \(N(19)<76\).
Grafos, Grupos y líneas equiangulares.
Si tenemos los vectores \((\mathbf{v_j})\) de las direcciones de un conjunto de lineas equiangulares la matriz de Gram correspondiente \(G=(\langle \mathbf{v_j}, \mathbf{v_k}\rangle)\) cuyos elementos son los productos escalares tiene la forma \(G=I-(\cos\alpha) S\) donde \(I\) es la matriz identidad y \(S\) tiene ceros en la diagonal y los demás elementos son todos iguales a \(1\) o \(-1\). Esta matriz determina y está determinada por un grafo de \(n\) vértices en el que \((j,k)\) es una arista precisamente cuando \(\langle \mathbf{v_j}, \mathbf{v_k}\rangle=-1\). Toda matriz de Gram es semidefinida positiva.
Esta relación es simétrica. Dado un grafo, sea \(S=(s_{j,k})\) su matriz de incidencia de Seidel, es decir, \(s_{j,k}=-1\) si \((j,k)\) es una arista del grafo y \(s_{j,k}=1\) si no. Si \(\theta\) es el menor autovalor de \(S\), la matriz \(G=I-\frac{1}{\theta}S\) es semidefinida positiva. Por tanto es la matriz de Gram de un conjunto de vectores unitarios. El rango \(n\) de la matriz es igual a \(v-k\) donde \(v\) es el número de vértices del grafo y \(k\) la multiplicidad de \(\theta\). Así que encontrar un conjunto de líneas equiangular equivale a encontrar un grafo peculiar. Un grafo tal que el menor autovalor de su matriz de adyacencia tenga una multiplicidad grande.
Los grafos asociados a conjuntos equiangulares son muy regulares. La teoría de grafos es una fuente importante de ejemplos de conjuntos equiangulares.
En los casos en que se conoce el valor exacto de \(N(n)\) el conjunto de lineas admite un grupo de simetrías que son grupos simples. Así en dimensión \(2\) el grupo es \(S_3\) el simétrico de 3 letras. En dimensión 3 el grupo es \(A_5\) el alternado de 5 letras. En dimensión 7 es el grupo \(Sp(6,2)\) el simpléctico de dimensión \(6\) sobre el cuerpo de característica \(2\).
Cotas inferiores y ángulos.
Un conjunto de líneas equiangulares equivale a un conjunto de vectores unitarios tales que sus productos escalares \(|\langle \mathbf{v_j},\mathbf{v_k}\rangle|=\cos\alpha\) es constante igual al coseno del ángulo que forman las líneas. El trabajo de Lemmens y Seidel no solo contiene el teorema de Gerzon, también contiene un teorema importante de Neumann
Teorema(Neumann [3]) Si tenemos un conjunto de \(N\) líneas equiangulares en \(\mathbf{R}^n\), y \(N>2n\), entonces el coseno del ángulo común vale \(\cos\alpha=\frac{1}{2k-1}\), con \(k\in\mathbf{N}\) un número natural.
Larman, Rogers y Seidel en 1977 refinan este resultado probando que además \(k<\frac{1 \sqrt{2n}}{2}\).
Estos resultados hacen interesante la cuestión de determinar \(N_\alpha(n)\) el número máximo de líneas equiangulares en \(\mathbf{R}^n\) formando justamente el ángulo \(\alpha\).
Es relativamente fácil probar que \(N(n)\ge c n^{3/2}\) para cierta constante $c$. Por mucho tiempo no se sabía el comportamiento asintótico de \(N(n)\). En el año 2000, D. de Caen [5] prueba que \(N(n)\ge \frac{2}{9}(n+1)^2\), para infinitos valores de \(n\). Del resultado de de Caen se sigue que \(N(n)>\frac{1}{72}(n+2)^2\) para todo \(n\). Gary Greaves et al posteriormente [6] han mejorado la constante de esta cota inferior.
La aportación de Igor Balla, Felix Dräxler, Peter Keevash, y Benny Sudakov.
Lo que me ha movido a tratar este tema es la aparición hace unos meses de un trabajo en la prestigiosa revista Inventiones Mathematicae.
En el ejemplo de de Caen y en otros ejemplos de conjuntos equiangulares de tamaño del orden de \(n^2\) el ángulo es del orden de \(\arccos(n^{-1/2})\). Mientras que todos los ejemplos extremales con dimensión pequeña tienen un ángulo mucho menor. Es por esto natural considerar el problema de determinar \(N_\alpha(n)\) dejando fijo \(\alpha\). Lemmens y Seidel preguntaron sobre \(N_\alpha(n)\) y probaron que para \(\cos\alpha=1/3\), se tiene \(N_\alpha(n)=2n-2\) si \(n\) es grande.
Se acaba de publicar la prueba por los autores citados antes del siguiente resultado.
Teorema:
Para \(\cos\alpha=\frac13\) se tiene \(N_\alpha(n)= 2n-2\) si \(n\) es suficientemente grande. Si \(\beta\in(0,\pi/2)\) es otro ángulo cualquiera se tiene \(N_\beta(n)\le 1.93 n\).
Igor Balla y Felix Dräxler son estudiantes de doctorado bajo la dirección de Benny Sudakov en el departamento de Matemáticas de ETH en Zürich. Peter Keevash es profesor en el Instituto de Matemáticas de la Universidad de Oxford. La demostración es una sinfonía de técnicas matemáticas, principalmente de la teoría de Grafos aplicados al problema de las líneas equiangulares.
Citas y el valor de un trabajo matemático.
El trabajo de Haantjes (1948) está publicado en una revista holandesa de poca difusión. No he podido consultarlo. Puede que este trabajo no tuviera mucha difusión por esto. Según MathSciNet lo han citado 11 artículos. Una cita es de 1971, las demás citas son todas posteriores a 2001.
El problema fue propuesto por van Lint y Seidel (1966). Está publicado también en una revista holandesa, pero esta vez Indagationes Mathematicae, una revista de reconocido prestigio. MathSciNet en este caso proporciona 51 referencias. De todos modos hay una referencia en 1971 y todas las demás posteriores a 2001.
Menos mal que el puesto de trabajo de van Lint y Seidel en 1966 no dependía de los métodos actuales de valoración por la ANECA. Está claro que su trabajo planteaba un problema importante. Daba importantes pasos para su solución. Hoy día es altamente citado, al cabo de 50 años de su publicación. Pero durante los primeros años las citas que pudo recibir eran principalmente de Seidel y sus colaboradores y fueron escasas.
Un trabajo matemático no debiera ser juzgado por la revista en que aparece publicado o las citas que recibe. Debe analizarse su aportación, y eso solo lo puede hacer un matemático que estudie, entienda y valore lo que se hace en el trabajo.
Bibliografía.
[1] Haantjes, J., Equilateral point-sets in elliptic two- and three-dimensional spaces, Nieuw Arch. Wiskunde (2) 22, (1948). 355-362.
[2] van Lint, J. H.; Seidel, J. J. Equilateral point sets in elliptic geometry, Nederl. Akad. Wetensch. Proc. Ser. A 69=Indag. Math. 28 (1966) 335-348.
[3] Lemmens, P. W. H.; Seidel, J. J., Equiangular lines, J. Algebra 24 (1973), 494-512.
[4] Larman, D. G.; Rogers, C. A.; Seidel, J. J., On two-distance sets in Euclidean space, Bull. London Math. Soc. 9 (1977), no. 3, 261–267.
[5] de Caen, D., Large equiangular sets of lines in Euclidean space, Electron. J. Combin. 7 (2000), Research Paper 55, 3 pp.
[6] Greaves, G.; Koolen, J. H.; Munemasa, Akihiro; Szöllösi, F., Equiangular lines in Euclidean spaces, J. Combin. Theory Ser. A 138 (2016), 208–235.
[7] Balla, Igor; Dräxler, Felix; Keevash, Peter; Sudakov, Benny; Equiangular lines and spherical codes in Euclidean space, Invent. Math. 211 (2018), no. 1, 179–212.
[8] Yu, Wei-Hsuan, There are no 76 equiangular lines in \(\mathbf{R}^{19}\), arXiv:1511.08569.
Hay una entrada en Quanta sobre el tema con una ilustración muy buena del caso \(n=3\). A New Path to Equal-Angle Lines


Dejar una contestacion