Solución: Billar a tres bandas

Publicamos la solución al divertimento Billar a tres bandas. Gracias a Alberto Castaño por la solución que ha aportado.

Divertimento:

El billar es un juego o deporte que permite plantear cuestiones interesantes. Hoy planteamos la siguiente. Consideramos una mesa de billar, \(OABC\), en la que \(OC=AB=2\) y \(OA=BC=1\). Tenemos la bola blanca en \(O\) y deseamos golpear la bola roja a tres bandas, es decir, la bola blanca debe tocar a la roja después de haber chocado contra tres bandas de la mesa. Así, por ejemplo, golpeamos con el taco la bola blanca, que debe chocar sucesivamente en \(AB\), \(BC\) y \(CO\) y a continuación tocar a la roja.

Supuesto que las bolas son puntuales y que se golpea sin efecto, preguntamos en qué región de la mesa se puede colocar la bola roja para que la bola blanca pueda llegar a ella.

(Indicación: Podemos poner un sistema cartesiano de modo que \(O=(0,0)\), \(A=(1,0)\), \(B=(1,2)\) y \(C=(0,2)\) y describir la región dando su frontera.)

Solución:

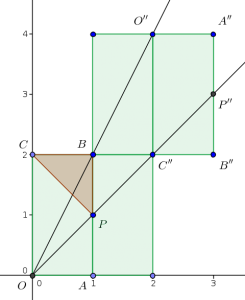
Las trayectorias de un movimiento que sigue la ley de la reflexión son líneas rectas cuando uno considera los recintos simétricos con respecto a la bandas contra las que choca la bola. Así, tras los tres choques, la bola entra dentro del rectángulo de vértices \(O»=(2,4)\), \(A»=(3,4)\), \(B»=(3,2)\) y \(C»=(2,2)\). Los puntos accesibles tras los tres choques son los puntos que se pueden unir con \(O\) mediante una recta contenida dentro de los rectángulos.

Así no son accesibles los puntos del triángulo \(C»B»P»\). La recta \(OP»\) tiene pendiente 1, de forma que \(P»\) es \((3,3)\). Por consiguiente, \(P»B»=PB=4-3=1\). Así, no son accesibles tras el choque a tres bandas los puntos del triángulo \(CBP\), siendo \(P=(1,1)\).