El cómo están dispuestos los ceros de la función zeta de Riemann parece cosa del diablo. Un trabajo aun no publicado de Brad Rodgers y Terence Tao nos lo muestra por enésima vez. Podemos resumir su trabajo diciendo que si la hipótesis de Riemann es verdadera, será por los pelos.
Preliminares sobre la función zeta
La función zeta se define para \(\text{Re}(s)>1\) mediante la serie de Dirichlet
$$\zeta(s)=\sum_{n=1}^\infty \frac{1}{n^s}.$$
Su conexión con los primos viene al menos de Euler que la usó para dar una prueba analítica de la infinitud de los primos. Pero fue Riemann quien la estudió a fondo. Riemann probó que se extiende como una función meromorfa a todo el plano con un único polo en \(s=1\). La función \(\zeta(s)\) se anula en los números pares negativos. Aparte de estos tiene infinitos ceros mucho mas misteriosos en la banda crítica (\(0<\text{Re} (s)<1\)). Riemann conjeturó que estos ceros estaban todos situados en la recta \(\text{Re}(s)=\frac12\). Hipótesis que no se ha podido probar hasta hoy y se conoce con el nombre de Hipótesis de Riemann (por brevedad escribiremos HR en lo que sigue).
Estos ceros intervienen en la fórmulas explícitas que expresan exactamente sumas dependientes de los primos, como \(\pi(x)\), el número de primos menores o iguales al número real y positivo \(x\).
Para estudiar los ceros Riemann construyó la función \(\Xi(z)\) definida por
$$\Xi(z):=\frac{s(s-1)}{2}\pi^{-s/2}\Gamma(s/2)\zeta(s), \qquad \text{donde \(s=\frac12+iz\)},$$ y \(\Gamma(s)\) es la función Gamma de Euler.
La función \(\Xi(z)\) es entera y tiene un cero por cada cero de \(\zeta(s)\) en la banda crítica y esos son sus únicos ceros. Así los ceros \(\frac12+i\gamma\) de \(\zeta(s)\) en la recta crítica se convierten en los ceros reales de la nueva función \(\Xi(\gamma)=0\). La HR equivale a que los ceros de esta función sean todos reales.
Además la función \(\Xi(t)\) gracias al factor normalizador \(\pi^{s/2}\Gamma(s/2)\) es real en el eje real. La función \(\Xi(t)\) para \(t\) real tiende a cero muy rápidamente. Por eso Riemann y todos los que después han calculado los ceros de \(\zeta(s)\) han usado la función \(Z(t)\).
Hay dos funciones real analíticas a valores reales \(\vartheta(t)\) y \(Z(t)\) tales que
$$\zeta(1/2+it)=e^{-i\vartheta(t)}Z(t).$$
Como \(Z(t)\) es real sus ceros se pueden detectar como cambios de signo. Y cada cero real de \(Z(t)\) corresponde a un cero de \(\zeta(s)\) justo en la recta crítica.

Precisamente todas las técnicas para ver que los ceros de \(\zeta(s)\) están en la recta \(\frac12+it\) se basan en detectar cambios de signo en \(Z(t)\). Se sabe que si \(Z(t)\) tiene un mínimo relativo positivo o un máximo relativo negativo, entonces HR es falsa.
The Bruijn-Newman constant
Riemann escribió la función \(\Xi(t)\) como una transformada de Fourier. Su resultado se puede escribir diciendo que
$$\frac18\Xi(t/2)=\int_0^\infty \Phi(u)\cos(tu)\,du$$
donde
$$\Phi(u)=\sum_{n=1}^\infty (2\pi^2n^4e^{9u}-3\pi n^2e^{5u})\exp(-\pi n^2e^{4u}).$$
Esta función es par \(\Phi(u)=\Phi(-u)\), pero la fórmula no nos lo dice. Hay que usar las propiedades de las formas modulares implicadas en la construcción de \(\Phi(u)\). Vemos ademas que \(\Phi(u)\) decrece super-exponencialmente a cero. De este modo la hipótesis de Riemann se transforma en la de probar que la transformada de Fourier de \(\Phi(u)\) tiene todos sus ceros reales.
Newman en 1976, basándose en trabajos anteriores de de Bruijn considera la función
$$H_t(z):=\int_0^\infty e^{tu^2}\Phi(u)\cos(zu)\,du.$$
Como \(H_0(x)=\Xi(x/2)/8\), la HR equivale a que todos los ceros de \(H_0(x)\) son reales.
En 1950 de Bruijn probó que \(H_t(x)\) tiene todos sus ceros reales para \(t\ge\frac12\) y que si \(H_{t_1}(x)\) tiene todos sus ceros reales y \(t_2>t_1\) entonces \(H_{t_2}(x)\) tiene también sus ceros reales.
El principal resultado de Newman es probar que existe una constante \(\Lambda\) (la constante de Bruijn-Newman) tal que los ceros de \(H_t(z)\) son todos reales precisamente cuando \(t\ge\Lambda\). Después de probar esta equivalencia en [3] Newman añade:
La hipótesis de Riemann equivale a la afirmación \(\Lambda\le0\); hacemos la conjetura complementaria de que \(\Lambda\ge 0\). Esta nueva conjetura es una versión cuantitativa del dicho de que la hipótesis de Riemann, si es verdadera, apenas lo es.
Es justo esta conjetura de Newman: \(\Lambda\ge0\) lo que acaban de probar Rodgers y Tao. Podemos decir que Rodgers y Tao han probado que si HR es verdadera lo será por los pelos.
Ecuación del calor retrógrada
Continuando con el trabajo de Newman tres matemáticos George Csordas, Wayne Smith y Richard Varga [6, 1994] dieron un impulso importante. Ellos estudiaron el comportamiento de los ceros de las funciones \(H_t(x)\).
Observan que la función \(H_t(x)\) verifica la ecuación del calor retrógrada
$$\frac{\partial H_t(x)}{\partial t}=-\frac{\partial^2 H_t(x)}{\partial x^2}.$$
Para \(t>\Lambda\) los ceros de \(H_t(x)\) son ceros simples, simétricos respecto del origen y no nulos. De manera que los positivos son
$$x_1(t)<x_2(t)<x_3(t)<\cdots $$
y con sus opuestos \(x_{-n}(t)=-x_n(t)\) son todos los ceros de \(H_t(x)\). Además evolucionan de acuerdo con el sistema de ecuaciones diferenciales
$$\frac{\partial x_n(t)}{\partial t}=\sum_{j\ne n}\frac{1}{x_j(t)-x_n(t)},$$
(entendiendo la suma como valor principal).
Antes de seguir con el desarrollo de Csordas y sus colaboradores, conviene conocer algunas observaciones realizadas anteriormente sobre los ceros de \(Z(t)\), es decir sobre los ceros de \(H_0(x)\) o equivalentemente los ceros de \(\zeta(s)\).
Lehmer y sus casi contraejemplos a HR
Ya Riemann trató de justificar numéricamente su hipótesis, probando que los primeros ceros de \(\zeta(s)\) están situados en la recta crítica. Pero cuando esto adquiere mas interés es con el advenimiento de los ordenadores. De hecho Alan Turing ya diseñó una máquina (que me recuerda a la clásica Antikythera) con ruedas dentadas, como un reloj que calculaba los primeros ceros. Y cuando tuvo a mano los primeros ordenadores calculó los primeros 1104 ceros con la esperanza de encontrar alguno fuera de la recta.
Después de Turing el siguiente en usar los ordenadores para calcular ceros y comprobar la HR fue Derrick Lehmer. El encontró el par de ceros extremadamente próximos
$$\rho_{6709}=\frac12+i\; 7005.06286\,61749\dots\quad \rho_{6710}=\frac12+i\; 7005.10056\,46726\dots$$
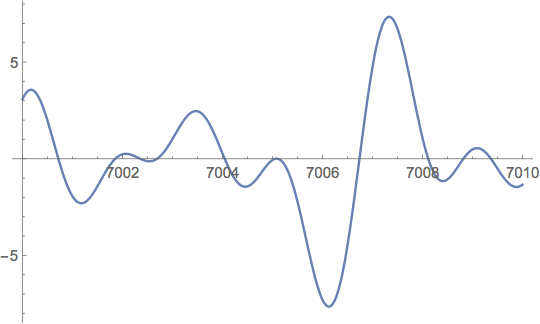
Como sabemos si el máximo de \(Z(t)\) cerca de \(t=7005\) fuera negativo, entonces la HR sería falsa. Por esto Lehmer señaló este par de ceros como un casi contraejemplo a HR.
Después otros investigadores encontraron otros muchos casi contraejemplos. Se trata de pares de ceros que están muy próximos en relación a los que tienen alrededor.
Esto es lo que lleva la información sobre los números primos. Los ceros del seno son los puntos \(\pi n\) con \(n\) entero. Están tan ordenados que prácticamente no llevan información, podemos describirlos en una línea. Pero los ceros de \(\zeta(s)\) son todo lo contrario, a veces juntos a veces muy separados y todo ello sin orden aparente.
El movimiento de los ceros
Los ceros determinan la función \(H _t(x)\). Csordas et al. prueban que
$$H_t(x)=H_t(0)\prod_{j=1}^\infty \Bigl(1-\frac{x^2}{x_j(t)^2}\Bigr).$$
La ecuación diferencial de los ceros informalmente indica que los ceros \(x_n(t)\) se repelen. Si en alguna región los ceros están mas concentrados tenderán a moverse hacia zonas menos densas al crecer \(t\). Moviéndose hacia una posición de equilibrio que está representada por una progresión aritmética.
De hecho \(e^{a^2 t}\sin(ax)\) tiene ceros \(\pi n/a\) en progresión aritmética y verifica la ecuación del calor retrógrada.
En su trabajo Csordas, Smith y Varga estudian la situación de los casi contraejemplos de Lehmer y ven que si dos ceros de una función \(H_t(x)\) están muy próximos en relación a los ceros cercanos, entonces tienden a separarse más cuando \(t\) aumenta. Es decir, cuando \(t\) aumenta los ceros tienden a situarse en progresión aritmética.
(Debemos decir que esto es solo una cuestión local en el sentido de que los ceros de \(H_t(x)\) para un \(t\) fijo tienden a estar más y más densamente situados cuando \(x\) crece).
El trabajo de Csordas et al. contiene una definición precisa de par de Lehmer. El par de ceros reales y consecutivos \(x_k(0)<x_{k+1}(0)\) de la función \(H_0(x)\) se dice que es un par de Lehmer si la diferencia \(\Delta_k=x_{k+1}(0)-x_k(0)\) satisface la desigualdad \(\Delta_k^2\cdot g_k(0)<4/5\) donde
$$g_k(0)=\sum_{j\ne k, k+1}\Bigl(\frac{1}{(x_k(0)-x_j(0))^2}+\frac{1}{(x_{k+1}(0)-x_j(0))^2}
\Bigr).$$
La gracia de la definición es que si tenemos un par de Lehmer podemos dar una cota inferior de la constante de Bruijn-Newman \(\lambda_k\le \Lambda\), siendo \(\lambda_k\) una función conocida de \(\Delta_k\) y \(g_k(0)\).
Usando los datos previos, proporcionados por Andrew Odlyzko, Csordas et al. detectan el par de Lehmer \((x_{1115578}, x_{1115579})\) prueban que \(\Lambda\ge-4.379\cdot 10^6\). Este límite mejoraba otros anteriores y ha sido superado varias veces. La última cota, obtenida en 2011 por el mismo método y usando un par de Lehmer mejor, es \(\Lambda\ge-1.15\cdot 10^{-11}\).
De la evolución de los ceros debemos decir que el caso más extremo, cuando \(H_t(x)\) tiene un cero doble real, se sigue que \(\Lambda\ge t\). También vemos que si \(H_0(x)\) tuviera, como los datos numéricos parecen sugerir, infinitos pares de Lehmer con \(g_k(0)\ge 0\), se seguiría que \(\Lambda\ge0\). Eso explica la frase de Newman. Si \(\Lambda\ge0\) quiere decir que \(H_0(x)\) tendría todos sus ceros reales, pero por los pelos, a duras penas.
Hugh Montgomery y la correlación de pares de zeros
Para poder entender el trabajo de Rodgers y Tao debemos volver atrás en el tiempo para describir los sorprendentes resultados de Montgomery sobre la distribución de los zeros de zeta.
Se llaman fórmulas explícitas en teoría de números a expresiones que igualan una suma en primos con una suma en los ceros de zeta. Para estudiar las correlaciones entre los ceros de zeta Hugh Montgomery (1972) parte de una de estas fórmulas explícitas
$$\sum_{p^k\le x}\frac{\log p}{p^s}=-\frac{\zeta'(s)}{\zeta(s)}+\frac{x^{1-s}}{1-s}-\sum_\rho\frac{x^{\rho-s}}{\rho-s}+\sum_{n=1}^\infty \frac{x^{-2n-s}}{2n+s}.$$
Montgomery supone la hipótesis de Riemann y considera para cada \(T>0\) grande el conjunto de las ordenadas de los ceros \(0<\gamma_n\le T\), tomando \(0<\gamma_1<\gamma_2<\cdots\). A medida que \(T\) aumenta esos ceros son cada vez mas densos, de manera que los normaliza tomando los números proporcionales \(x_n=\frac{\gamma_n\log T}{2\pi}\). Los nuevos números \(x_n\) están distribuidos como los \(\gamma_n\) pero su distancia media es \(1\). Y estudia ahora las correlaciones, esto es, la distribución de las diferencias \(x_n-x_m\) con \(n>m\).
El número de estos ceros hasta la altura \(T\) son del orden de \(\frac{T}{2\pi}\log T\). Lo que Montgomery prueba es que se cumple
$$\lim_{T\to\infty}\frac{\text{cardinal}\{(n,m)\colon \alpha<x_n-x_m<\beta\}}{\frac{T}{2\pi}\log T}=
\int_\alpha^\beta\Bigl[1-\Bigl(\frac{\sin \pi u}{\pi u}\Bigr)^2\Bigr]\,du$$
Vemos que las diferencias de los ceros no se distribuyen uniformemente sino que hay diferencias más o menos probables.
Se ha contado muchas veces la historia de cómo el físico F. Dyson explicó a Montgomery que esta era la correlación de los autovalores de una matriz unitaria aleatoria gausiana. Esto conectaba con la sugerencia de Hilbert-Pólya de que las ordenadas \(\gamma_n\) de los ceros de zeta deberían ser los autovalores de una matriz unitaria y que ese sería el camino de una demostración de la HR. Esto llevo a la conjetura GUE (Gaussian Unitary Ensamble) sobre la distribución de los ceros de zeta y que ha movido desde entonces las investigaciones sobre los ceros.
La conjetura GUE no está probada hoy día, pero los resultados de Montgomery, menos ambiciosos si están demostrados si admitimos la HR. Hay unas figuras obtenidas por Odlyzko que son espectaculares sobre esta distribución.
El trabajo de Rodgers y Tao

Rodgers y Tao prueban (sin admitir ninguna hipótesis adicional) la conjetura de Newman \(\Lambda\ge0\). La prueba es por reducción al absurdo. Supongamos que \(\Lambda<0\), entonces por el resultado de Newman \(H_0(x)\) tendrá todos sus ceros reales. Por tanto la HR sería válida. Y podemos admitirla en todo el razonamiento por reducción al absurdo.
Como \(\Lambda<0\) la ecuación del movimiento de las \(x_n(t)\) tiene un intervalo de tiempo en que actuar desde \(t=\Lambda\) hasta el valor \(t=0\). Por tanto cabe pensar que sus ceros estarán relativamente próximos a la posición de equilibrio. Pero eso contradice los resultados de Montgomery.

Naturalmente hay que hacer cuantitativas las aserciones anteriores. Nada fácil, el trabajo de Rodgers y Tao tiene 44 páginas.
En primer lugar refinan el análisis de Csordas et al. y consiguen una cota superior del espacio entre ceros consecutivos
$$\log\frac{1}{|x_{n+1}(t)-x_n(t)|}\ll (\log n)^2\log\log n,\qquad n\ge n_0, \quad \Lambda/2\le t\le 0.$$
Esto casi les permite definir el Hamiltoniano del sistema
$${\mathcal H}(t)=\sum_{n\ne m}\log\frac{1}{|x_{m}(t)-x_n(t)|}.$$
El argumento es intrincado. Al final llegan a probar que
$$x_{n+1}(0)-x_n(0)=\frac{4\pi+o_{T\to\infty}(1)}{\log T}$$
para una fracción \(1-o(1)\) de \(n\in [T\log T, 2T\log T]\). Como estos \(x_j(0)\) son proporcionales a las ordenadas de los ceros de \(\zeta(s)\), esto implica que los huecos entre los ceros de la función zeta son raramente mucho mayores que su valor medio. Mientras que lo opuesto es afirmado por Montgomery en [2]. La prueba completa de esta afirmación de Montgomery puede encontrarse en el trabajo de Conrey et al. [4]. Ellos prueban que para cualquier \(\lambda>0.77\) existe una constante \(c(\lambda)>0\) tal que al menos una proporción \(c(\lambda)\) de \(n\le T\log T\) satisfacen
$$x_{n+1}(0)-x_n(0)\le \lambda\frac{4\pi}{\log T}.$$
La contradicción prueba que \(\Lambda\ge0\).
Polymath 15
Los resultados anteriores a primera vista hacen pensar que la prueba de la HR está ahora más lejos que nunca. Si la HR es cierta, la más ligera perturbación de la función \(H_0(t)\) hará que aparezcan ceros complejos. Posiblemente hay o algún cero doble o una infinidad de pares de Lehmer cada vez más extremos.
Esta irregularidad de los ceros siempre ha sido la principal dificultad para probar HR. No parece que pueda existir ninguna aproximación asintótica a \(\Xi(t)\) o a \(Z(t)\) que impliquen que los ceros sean reales, ni siquiera que la mayor parte de los ceros son reales. Los métodos actuales no consiguen probar ni siquiera que el 50% de los ceros de \(\zeta(s)\) están en la recta crítica.
Sin embargo Tao no parece haber tirado la toalla. El 24 de enero pasado Tao ha propuesto un nuevo proyecto Polymath.
Proyecto Polymath 15: Upper bounding the de Bruijn-Newman constant
Hasta ahora se sabe que \(0\le \Lambda<1/2\). de Bruijn probó que \(\Lambda\le 1/2\) y H. Ki et al. probaron que en realidad \(\Lambda<1/2\). Tao propone mejorar la cota superior de \(\Lambda\).
Tao afirma que no espera que se consiga probar la hipótesis de Riemann por este camino, pero avanzar nuestro conocimiento sobre las funciones \(H_t(z)\) y mejorar la cota de \(\Lambda\) sí parecen objetivos realistas.
Yo sí que creo que puede ser un camino interesante. Cualquier función \(H_t(x)\) con \(t>0\) es esencialmente mas simple que \(H_0(x)\). Bastaría probar que todas ellas tienen ceros reales para conseguir probar HR. Puede que cada \(H_t(x)\), con \(t>0\), sea esencialmente más simple que todo HR. Y nunca ha habido tan buenos matemáticos detrás de conseguirlo.
Sobre Polymath
Polymath Project es una colaboración entre matemáticos para resolver problemas importantes y difíciles, mediante la colaboración en la web. El proyecto empezó en Enero de 2009 cuando Tim Gowers en su blog invitó a sus lectores a subir ideas parciales y progresos hacia la solución de un problema concreto que propuso. El éxito del proyecto hizo que continuaran añadiéndose nuevos proyectos. El actual de Tao es el número 15. Información sobre ellos se puede encontrar en la wiki: wiki for polymath projects.
Para saber más
Blog de Terence Tao explicando su resultado.
Un entrada del blog: La ciencia de la mula francis
Página de Wikipedia sobre la constante de Bruijn-Newman.
Información sobre la ecuación del calor retrógrada
El trabajo de B. Rodgers y Terence Tao
Finalmente los trabajos que hemos citado:
[1] de Bruijn, N. G. The roots of trigonometric integrals. Duke Math. J. 17, (1950). 197-226.
[2] Montgomery, H. L. The pair correlation of zeros of the zeta function. Analytic number theory (Proc. Sympos. Pure Math., Vol. XXIV, St. Louis Univ., St. Louis, Mo., 1972), pp. 181–193. Amer. Math. Soc., Providence, R.I., 1973.
[3] Newman, C. M. Fourier transforms with only real zeros. Proc. Amer. Math. Soc. 61 (1976), no. 2, 245-251 (1977).
[4] Conrey, J. B.; Ghosh, A.; Goldston, D.; Gonek, S. M.; Heath-Brown, D. R., On the distribution of gaps between zeros of the zeta-function. Quart. J. Math. Oxford Ser. (2) 36 (1985), no. 141, 43-51.
[5] Odlyzko, A. M. On the distribution of spacings between zeros of the zeta function. Math. Comp. 48 (1987), no. 177, 273-308.
[6] Csordas, G.; Smith, W.; Varga, R. S., Lehmer pairs of zeros, the de Bruijn-Newman constant \(\Lambda\), and the Riemann hypothesis. Constr. Approx. 10 (1994), no. 1, 107–129.
[7] H. Ki; Y. O. Kim; J. Lee, On the de Bruijn-Newman constant, Advances in Mathematics, 22 (2009), 281–306.
[8] Rodgers, B.; Tao, T., The de Bruijn-Newman constant is non-negative, arXiv 1801.05914, January 2018.

Dejar una contestacion