Solución: El viaje del Beagle

Publicamos la solución al divertimento El viaje del Beagle. Gracias a Cristóbal Sánchez-Rubio por la solución que ha enviado.

Divertimento:

Supongamos que la Tierra es una esfera cuyo radio es 6.366 km (adoptando el criterio de que el meridiano tiene 40.000 km). Se pide averiguar si el Beagle en el viaje de Darwin pudo llegar desde las Islas Galápagos hasta Tahití en menos de 6.500 km, sabiendo que las coordenadas geográficas de las Galápagos son 0º49’45’’S y 90º58’55’’O y las de Tahití son 17º32’14’’S y 149º33’59’’O.

Supongamos ahora que tenemos dos puntos distintos del hemisferio norte que se encuentran en el mismo paralelo y cuyas longitudes tienen una diferencia de \(\pi/2\) radianes. Es frecuente pensar que la mínima distancia entre ellos es la que hay si nos desplazamos del uno al otro por el paralelo, y sin embargo no es así. ¿Para qué latitud es máxima la diferencia entre la distancia que hay siguiendo el paralelo y la que hay siguiendo la circunferencia máxima?¿Cuánto vale dicha diferencia?

Solución:

Solución propuesta por Cristóbal Sánchez-Rubio.

La primera cuestión es un simple cálculo de triángulos esféricos. En el triángulo GTS (Galápagos, Tahití, Polo Sur) conocemos el ángulo diedro \(S\) que es la diferencia de longitudes y los lados \(g\), \(t\) que son los ángulos suplementarios de las latitudes de Galápagos y Tahití.

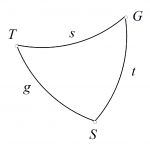
Usaremos el teorema del coseno $$\cos S = \cos G  \cos T + \sin S  \sin T \cos S.$$ Pasando los ángulos a radianes y llamando \(R\) al radio de la tierra queda $$\cos S = 0,501323268.$$ La longitud del trayecto es $$R  \arccos (0,50132327) = 6656,728205. $$ Parece que no pudo llegar recorriendo menos de 6500 Km.

Para la segunda cuestión hay que comparar la longitud de un arco de paralelo con la de un arco de círculo máximo que une los mismos. Llamando \(x\) a la latitud del paralelo considerado, \(A\) y \(B\) los extremos del arco de paralelo de amplitud \({\pi }/{2}\), el radio del paralelo es \(R \cos x\) y su longitud \(p\) es $$p = R\frac{\pi }{2}\cos x.$$ Si \(N\) es Polo norte, en el triángulo NAB (figura de la derecha) 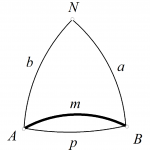y con la misma fórmula anterior, para el lado \(m\) resulta $$\cos m = \sin^2x \Rightarrow m = R \arccos \left( \sin^2x \right),$$ ya que los lados \(a\) y \(b\) son el complemento de la latitud \(x\). La diferencia de ambos trayectos es $$p – m = R\frac{\pi }{2}\cos x – R \arccos \left( {\sin^2x} \right)$$ que es nula evidentemente en el Ecuador y en el Polo norte. Prescindiendo del factor constante \(R\), se trata de hallar el máximo de $$
f\left( x \right) = \frac{\pi }{2}\cos x – \arccos \left( {\sin^2x}
\right), \qquad \left( {0 \le x \le \frac{\pi }{2}} \right).
$$ El resto es puro cálculo cuyo detalle se omite, la ecuación $$f’\left( x \right) = – \frac{\pi \sin x}{2} – \frac{2 \sin x \cos x}{\sqrt {1 – \sin^4x} } = 0$$ después de operar y simplificar, resulta $$x = \frac{\sqrt {16 – \pi ^2} }{\pi } \simeq \mbox{0,78812368}.$$

Aproximadamente 45 grados. La diferencia es 421,7508025 Km.