Lo que mas chocaría a Gauss si volviera a la vida sería saber que los estudios que hizo para determinar la excentricidad del asteroide Juno (0.254236) se usan hoy día para multiplicar números naturales.
Esa sorpresa la vivió en primera persona Kolmogórov. En los años 50, cuando tenía unos 50 años, influido por los trabajos de Wiener y Claude Shannon, se interesó por los algoritmos de computación, fue de los primeros en interesarse por la complejidad de los algoritmos.
Kolmogórov se planteó el problema de cuantificar el trabajo de efectuar un algoritmo. ¿Cuánto mas cuesta multiplicar dos números de \(n\) cifras que sumarlos? La respuesta es contar cuantas operaciones elementales tenemos que realizar. Podríamos dar una definición precisa de qué es una operación elemental, pero creo que en lo que sigue serán suficientes las ideas intuitivas que tenemos.

Para sumar los dos números tenemos que leer cada cifra (pues al modificar una sola el resultado cambiaría), son \(2n\) operaciones y tenemos que escribir el resultado, otras \(n\) operaciones. El trabajo con cada par de cifras es mas o menos constante. De este modo vemos que el número \(S(n)\) de operaciones necesarias para sumar dos números de \(n\) dígitos verifica las acotaciones \(2n\le S(n)\le C\;n\) donde \(C\) es cierta constante. Diremos que el número de operaciones necesarias para la suma es \(S(n)=O(n)\). Esto es, del orden de \(n\) operaciones.
¿Qué ocurre con el producto? Denotemos por \(M(n)\) el orden de operaciones elementales necesarias para multiplicar números de \(n\) cifras con el mejor algoritmo posible. Tenemos también que \(M(n)\ge 2n\) porque los números, al menos, hay que leerlos. En el algoritmo que aprendemos en la escuela debemos hacer una operación elemental con cada pareja de dígitos, uno del multiplicando y otro del multiplicador. Son \(n^2\) parejas. El trabajo restante es de orden menor. De manera que llegamos a que el algoritmo usual prueba que \(M(n)\le c n^2\).
El algoritmo usual es muy antiguo. Tanto, que en realidad no sabemos cuándo se originó. Un algoritmo semejante existía en tiempos de los sumerios o egipcios, hace unos 4000 años, y posiblemente viene de más atrás en el tiempo. Kolmogórov pensaba que si existiese otro algoritmo mejor ya habría sido descubierto. En sus seminarios planteaba la hipótesis de que \(M(n)=O(n^2)\). Esto es, que el mejor método para multiplicar números de longitud \(n\) necesitaría del orden de \(n^2\) operaciones elementales.

Anatoli Karatsuba, un alumno de Kolmogórov, con 23 años en aquel momento, cuenta en [2] lo que sucedió:
En el otoño de 1960 tuvo lugar un seminario sobre problemas en cibernética en la Facultad de Mecánica y Matemáticas de la Universidad de Moscú bajo la dirección de Kolmogórov. En ella, Kolmogórov enunció la conjetura \(n^2\) y propuso algunos problemas relativos a la complejidad de la solución de sistemas lineales de ecuaciones y algunos cálculos similares. Comencé a pensar activamente sobre la conjetura \(n^2\), y en menos de una semana encontré que el algoritmo con el que pensaba deducir una cota inferior para \(M(n)\) proporcionaba una cota de la forma
$$M(n)=O(n^{\log_23}),\qquad \log_23=1,\!5849\dots$$
Al finalizar la siguiente reunión del seminario le conté a Kolmogórov el nuevo algoritmo y la refutación de la conjetura \(n^2\). Kolmogórov estaba muy agitado porque esto contradecía su muy plausible conjetura. En la siguiente reunión del seminario, Kolmogórov mismo contó a los participantes acerca de mi método y en este punto el seminario acabó.
Son 4000 años vencidos en una semana por una mente joven, abierta, frente a un problema bien propuesto. Es interesante el análisis. Kolmogórov se planteó el problema de determinar el orden de \(M(n)\). En los 4000 años anteriores se había buscado un buen método y se había encontrado. Gauss, por ejemplo, no se planteó mejorarlo, era un buen método y rara vez se tenían que multiplicar números de muchos dígitos. Pero Kolmogórov planteó el problema de ver que no hay otro método mejor, probar que \(M(n)\ge cn^2\). Es decir, propuso probar que no importa el método que usemos, necesitaremos del orden de \(n^2\) operaciones elementales.
Entonces llegó Karatsuba con su mente abierta y trató de probar la conjetura de Kolmogórov. ¿Cómo hacerlo? Su estrategia fue suponer conocido \(M(n)\) y trató de encontrar una relación entre \(M(n)\) y \(M(n/2)\). Entonces hay otra cuestión. Si sé multiplicar números de \(n/2\) cifras, ¿en qué me ayuda esto para multiplicar números de \(2n\) cifras? Como veremos, esto lleva directamente al nuevo algoritmo.
Buenas preguntas y mente abierta son dos de los ingredientes de las matemáticas.
El algoritmo de Karatsuba
El algoritmo de Karatsuba es un ejemplo de la estrategia general divide y vencerás. La idea es simple: sean \(A\) y \(B\) los números a multiplicar con \(2n\) cifras; los separamos en grupos de \(n\) cifras
$$A=A_1 10^n+A_0,\quad B=B_110^n+B_0.$$
entonces
$$AB=(A_1 10^n+A_0)(B_110^n+B_0)=A_1B_1 10^{2n}+(A_1B_0+A_0B_1)10^n+A_0 B_0.$$
Notemos que
$$A_1B_0+A_0B_1=(A_1-A_0)(B_0-B_1)+A_1B_1+A_0B_0.$$
De manera que obtenemos
$$AB=(10^{2n}+10^n)A_1B_1+10^n(A_1-A_0)(B_0-B_1)+(10^n+1)A_0B_0$$
Hemos reducido así el producto de dos números de \(2n\) dígitos a tres productos de números de \(n\) dígitos \(A_1B_1\), \(A_0B_0\) y \((A_1-A_0)(B_0-B_1)\), más unas cuantas traslaciones y sumas. Luego hemos probado que
$$M(2n)\le 3M(n)+8S(n)\le 3M(n)+a\,n,$$
para cierta constante \(a\). Por inducción probamos que para una potencia de dos \(n=2^m\) se tiene
$$M(2^m)\le M(1) 3^m +a(2^m+2^{m-1}3+2^{m-2}3^2+\cdots +2\cdot 3^{m-1})$$
y siendo \(2^\alpha=3\), esto es, \(\alpha=\log_23\), obtenemos
$$M(2^m)\le 3^m(M(1)+2a)=C\, 2^{\alpha m}=C(2^m)^\alpha.$$
Ahora para cualquier \(n\), existe \(m\) tal que \(2^{m-1}\le n<2^m\) y cualquier número de \(n\) dígitos puede considerarse un número de \(2^m\) dígitos, luego
$$M(n)\le M(2^m)\le C(2^{m})^\alpha=C2^\alpha (2^{m-1})^\alpha\le 3C n^\alpha.$$
Esto es una versión del método de Karatsuba, simplificando para la exposición el método contenido en [2].
Nuevos progresos, el algoritmo de Schönhage-Strassen

Después de la sorpresa de Karatsuba quedó planteado el problema del verdadero orden de \(M(n)\). Toom y Cook (1966) extendieron las ideas de Karatsuba y consiguieron probar que \(M(n)=O(n(\log n) e^{c\sqrt{\log n}})\). Nos centraremos en lo que sigue en explicar el método de Schönhage-Strassen (1971), que es el que se usa en la práctica hoy en día cuando se quieren multiplicar números realmente grandes, por ejemplo con cientos de miles o hasta billones de dígitos.
Todos los métodos conocidos se basan en una idea:
Multiplicar números es equivalente a multiplicar polinomios.
Los factores están escritos en una base, realmente los métodos de multiplicación usan la base \(2\), pero lo ilustramos con nuestra base decimal que nos es más familiar. La notación 325 por ejemplo significa
$$3\times 10^2+2\times 10+5=p(10), \quad\text{donde}\quad
p(x)=3x^2+2x+5.$$
Y multiplicar dos números es casi equivalente a multiplicar dos polinomios. Por ejemplo
$$\begin{array}{lllll}
& & 3 & 2 & 5\\
& & 2 & 7 & 3\\ \hline
& & 9 & 7 & 5\\
2 & 2 & 7 & 5 & \\
6 & 5 & 0 & & \\ \hline
8 & 8 & 7 & 2 & 5
\end{array}
\qquad\qquad
\begin{array}{rrrrr}
& & 3x^2 & +2x & +5\\
& & 2x^2 & +7x & +3\\ \hline
& & 9x^2 & +6x & +15\\
& 21x^3 & +14x^2 & +35x & \\
6x^4 & +4x^3 & +10x^2 & & \\ \hline
6x^4 & +25x^3 & +33x^2 & +41 x & 15
\end{array}
$$
El producto de polinomios es mas ordenado, no hay transferencias de una columna a otra. Además es prácticamente equivalente pues el polinomio producto evaluado en \(x=10\) nos da el valor del producto de los números. De hecho conociendo los coeficientes del polinomio producto, se puede obtener el producto, como se ve en el siguiente diagrama.
$$\begin{array}{lllll}
& & & 1 & 5\\
& & 4 & 1 & \\
& 3 & 3 & & \\
2 & 5 & & & \\
6 & & & & \\ \hline
8 & 8 & 7 & 2 & 5
\end{array}
$$
Los coeficientes del polinomio producto serán menores que \(nb^2\) si estamos trabajando en base \(b\), y el número de operaciones elementales para obtener el producto a partir del polinomio será aproximadamente \(n\log(nb^2)\).
En el método de Schönhage-Strassen, si queremos multiplicar números de \(n\) dígitos binarios, se buscan números \(k\) y \(\ell\) tales que \(2n\le 2^k \ell<4n\) y entonces trabajamos con números de \(2^k\) dígitos en base \(b=2^\ell\). De este modo, obtenido el producto de los polinomios, necesitamos \(2^k \log(2^k 2^{2\ell})\approx 2^k(k+2\ell)\). Tomando \(k\) y \(\ell\) del mismo orden conseguimos obtener el producto con \(O(n)\) operaciones elementales, suponiendo conocido el producto de polinomios.
Convolución y Transformada de Fourier
Recordemos que para multiplicar números de \(n\) dígitos escogemos \(2n\le 2^k \ell<4n\) y trabajamos en base \(b=2^\ell\), es decir agrupando las cifras de los factores en grupos de \(\ell\) dígitos binarios.
Los factores tendrán aproximadamente \(n/\ell<2^{k-1}\) dígitos en base \(2^\ell\). Definiendo \(K=2^k\) podremos escribir los factores en la base \(b\) en la forma
$$(U_{K-1}, U_{K-2},\dots, U_0)_b, \quad (V_{K-1}, V_{K-2},\dots, V_0)_b.$$
Como eran números de menos de \(K/2\) cifras, tendremos \(U_j=V_j\) para \(j\ge K/2\). Eso lo hemos hecho intencionadamente por lo que sigue.
Debemos calcular los coeficientes del polinomio producto
$$\begin{array}{rl}P(x)&=U(x)V(x)\\&=(U_{K-1}x^{K-1}+U_{K-2}x^{K-2}+\cdots +U_1x+U_0)
(V_{K-1}x^{K-1}+V_{K-2}x^{K-2}+\cdots +V_1x+V_0),\end{array}$$
que son los números
$$P_r=U_rV_0+U_{r-1}V_1+\cdots + U_0V_r$$
gracias a que hemos añadido los \(U_j=V_j=0\) para los \(j\) grandes. Se tiene que esto es igual a la convolución en el grupo \(\mathbf{Z}/(K\mathbf{Z})\) de los números modulo \(K\), es decir, que
$$P_r=\sum_{a+b=r} U_aV_b.$$
La operación de convolución está estrechamente relacionada con la transformada de Fourier. En el caso del grupo finito \(\mathbf{Z}/(K\mathbf{Z})\) la trasformada de \((U_j)_{j=0}^K\) es la sucesión
$$
\widehat{U}_a=\sum_{j=0}^{K-1} U_j \omega^{aj},\qquad \omega=e^{-2\pi i/K}.\qquad (1)
$$
Es decir,
$$\widehat{U}_a=U(\omega^a),\quad \widehat{V}_a=V(\omega^a)$$
son los valores de los polinomios \(U(x)\) y \(V(x)\) en las raíces de la unidad.
De esto se sigue la propiedad fundamental de la transformada y la convolución. Debido a que el polinomio \(P(x)=U(x)V(x)\), tendremos que la transformada de la convolución es el producto de las transformadas
$$P(\omega^a)=U(\omega^a)V(\omega^a),\quad\text{esto es}\quad\widehat{P}_a=\widehat{U}_a\widehat{V}_a.$$
Así que, no los coeficientes \(P_a\), pero sí sus transformados de Fourier, se obtienen fácilmente mediante tan solo \(K\) productos.
Al rescate viene entonces el hecho de que la inversa de la transformada es esencialmente otra transformada de Fourier:
$$P_a=\frac{1}{K}\sum_{j=0}^{K-1}\widehat{P}_a\omega^{-aj}.$$
Tenemos entonces el siguiente esquema para multiplicar números. Encontrar la transformada de Fourier de los factores \(\widehat{U}_a\) y \(\widehat{V}_a\). Formar \(K\) productos \(\widehat{P}_a=\widehat{U}_a\widehat{V}_a\) y realizar una nueva transformada de Fourier (inversa) para obtener los coeficientes del producto.
El problema es que tal como hemos definido la transformada en (1), necesitamos \(K^2\) productos, y esto es demasiado grande. En este punto nos ayuda una técnica que ya era conocida por Gauss pero que fue redescubierta y popularizada en Cooley y Tukey en 1965.
Transformada de Fourier rápida
La técnica de la FFT (Fast Fourier Transform) es complicada. Su utilidad práctica se extiende a muchos campos de la técnica. Cualquier procedimiento en que se aplique la transformada de Fourier se aprovecha de ella. Gauss [1] la estudio en relación a sus cálculos astronómicos. Gauss quería determinar la órbita de un asteroide a partir de una serie de mediciones. Expresaba la órbita como una serie trigonométrica y deseaba obtener los coeficientes a partir de las mediciones. Esto es en realidad una transformada de Fourier.
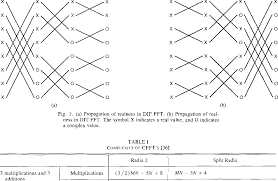
FFT se basa en la identidad de Danielson-Lanczos. Suponiendo \(K\) par, se tiene
$$\widehat{U}_a=\sum_{j=0}^{K-1} U_j \omega^{aj}=\sum_{j=0}^{K/2-1}U_{2j} (\omega^2)^{aj}
+\omega^a\sum_{j=0}^{K/2-1}U_{2j+1} (\omega^2)^{aj}.$$
Esta igualdad expresa una transformada de Fourier, que requiere \(K^2\) productos, mediante dos transformadas de longitud mitad que requieren \(2(K/2)^2=K^2/2\) multiplicaciones. Si \(K\) es una potencia de dos, podemos iterar el procedimiento y al final obtenemos un método de calcular la transformada que tan solo requiere \(O(K\log K)\) operaciones.
Repito que hay libros enteros dedicados a la técnica FFT y que por tanto a nuestra explicación, siendo correcta, le faltan algunos detalles.
El Álgebra y el juego de los anillos
Llegamos al último ingrediente del método de Schönhage-Strassen. Tal como lo hemos descrito ha sido implementada con éxito. En ella se ha usado el anillo de los números complejos. La raíz de la unidad \(\omega\) es un número complejo, los cálculos han de hacerse en \(\mathbf{C}\) y las transformadas \(\widehat{U}_j\) son números complejos. Esto hace necesario trabajar con números aproximados y requiere un estudio riguroso de los errores, aparte de que hay un poco de suerte en que los errores no se propagan demasiado en los cálculos a realizar.
Pero es posible sustituir el cuerpo \(\mathbf{C}\) por un anillo en que tengamos una raíz primitiva \(K\)-ésima de la unidad y en el que \(K\) sea invertible. Con ello podremos definir la transformada sustituyendo el número complejo \(\omega\) por la raíz de la unidad. Las fórmulas anteriores siguen siendo válidas.
Por ejemplo, uno puede usar el anillo \(\mathbf{Z}((2^m+1)\mathbf{Z})\) tomando \(m>k+2\ell\). De este modo los números \(P_a\mod (2^m+1)\) permiten recuperar \(P_a\) ya que \(P_a<2^m\).
Tomamos \(m\) que sea multiplo de \(K\), de este modo \(\omega=2^{2m/K}\) es una raíz primitiva de la unidad de orden \(K\). La elección dado \(n\) de \(k\), \(\ell\) \(K\), y \(m\) es uno de los problemas prácticos del método de Schönhage-Strassen. Pero unas buenas elecciones garantizan que el método se realiza con \(O(n\log n\log\log n)\) operaciones elementales.
Avances posteriores sobre el valor de M(n)
La conjetura de Kolmogorov no era válida, y el resultado de Karatsuba lo demuestra. Pero entonces ¿cuál es el verdadero orden de \(M(n)\)? No lo sabemos, desde el resultado de Karatsuba se han ido construyendo mejores algoritmos que rebajan la cota superior de \(M(n)\). Los avances posteriores al método de Schönhage-Strassen no han tenido repercusión práctica. En primer lugar son solo modificaciones, podemos decir que ligeras, del método de Schönhage-Strassen del que se separan principalmente en la elección de anillo o anillos en los que se trabaja.
Segundo, los avances se refieren al último factor en \(n\log n\log\log n\). Es sustituido por otro factor que crece más lentamente, pero dado que \(\log\log n\) crece tan lento, la ventaja no tendría lugar más que para números que realmente no están al alcance de los ordenadores actuales.
Para explicar hasta dónde llegan estas mejoras, debemos definir una función muy lenta, extremadamente lenta: \(\log^*x\), definida para \(x\ge1\). Dado \(x>1\), pongamos \(x_0=x\), \(x_1=\log x\), \(x_2=\log x_1\), \(\dots\), \(x_n=\log x_{n-1}\), parando en el momento que encontremos el primer \(x_n\le 1\). Entonces definimos \(\log^*x=n\). La función \(\log^* x\) vale \(1\) en el intervalo \((1,e]\), \(\log^*x=2\) para \(x\in(e,e^e]\), \(\log^*x=3\) para \(x\in(e^e, e^{e^e}]\), \(\dots\) vale \(4\) cuando \(x\) tiene menos de 1656520 dígitos. La función \(\log^*x\) tiende a infinito pero de la manera mas perezosa imaginable (si no fuéramos matemáticos, que tenemos una imaginación inimaginable).
Ahora estamos en condiciones de explicar la evolución de nuestro conocimiento sobre \(M(n)\).
Hemos escrito esta entrada con motivo de la aparición del trabajo de Harvey, y van der Hoeven [11] en arXiv en febrero de este año. En trabajos anteriores se había conseguido la multiplicación en \(O(n\log n\; 4^{\log^*n})\) operaciones elementales, pero suponiendo la existencia de ciertos primos que eran necesarios para construir los anillos en que se trabajaba. Esto hacía el resultado condicional, porque aunque los primos adecuados se supone que existen, eso no estaba probado. En este trabajo se obtienen anillos adecuados sin necesidad de hacer hipótesis sobre la existencia de ciertos números primos.
Hay una pregunta que no quiero dejar de formular antes de terminar la entrada.
Problema 1. ¿Es realmente \(M(n)\ge C n\log n\)?
Para la suma conocemos el orden exacto ya que es claro que \(S(n)>Cn\), porque al menos tenemos que leer los datos, y el método usual de suma da una cota superior del mismo orden. En nuestra cuestión es necesario considerar cualquier método posible para multiplicar y ver que todos necesitan hacer del orden de \(n\log n\) operaciones elementales. Este tipo de problemas son actualmente muy difíciles.
Para saber más
El aspecto histórico de como Gauss fue el primero en definir la técnica de la FFT se encuentra bien desarrollado en
[1] Heideman, M.T., Johnson, D.H., y Burrus, C. S., Gauss and the History of the Fast Fourier Transform, IEEE ASSP Magazine 1 (4) (1984) 14-21.
Copia en pdf.
La historia de Karatsuba la he sacado de
[2] Karatsuba, A. A., The Complexity of computations, Proc. Steklov Inst. Math., 211 (1995), 169-183.
Pdf del artículo.
Esta historia tiene una segunda parte, un tanto desgraciada. Karatsuba lo cuenta, pero podemos ver algunos detalles y/o comentarios en:
[3] Pregunta sobre la relación Kolmogórov-Karatsuba en Stackexchange sobre teoría de la computación.
El método de Schönhage-Strassen está expuesto en diversas fuentes. Recomendamos especialmente
[4] Knuth, D. E. The art of computer programming. Vol. 2. Seminumerical algorithms, Third edition. Addison-Wesley, Reading, MA, 1998.
o también
[5] Crandall, R., Pomerance, C., Prime numbers. A computational perspective, Second edition. Springer, New York, 2005.
El trabajo original está escrito en alemán:
[6] Schönhage, A.; Strassen, V., Schnelle Multiplikation grosser Zahlen, Computing (Arch. Elektron. Rechnen) 7 (1971), 281-292.
Para el que desee información en detalle puede ser útil
[7] Gaudry, P., Kruppa, A., Zimmermann, P., A GMP-based implementation of Schönhage-Strassen’s large integer multiplication algorithm, ISSAC 2007, 167–174, ACM, New York, 2007. Pdf del artículo.
Otros trabajos que he consultado para esta entrada:
[8] Pollard, J. M., The Fast Fourier Transform in a Finite Field, Math. of Comp. 25, (1971) 365-374. Pdf del artículo.
[9] Toom, A. L., The complexity of a scheme of functional elements simulating the multiplication of integers, Soviet Math. Dokl., 3 (1963) 714–716.
El pdf del artículo puede encontrase en su página web con algún otro material interesante.
[10] Fürer, M., Faster integer multiplication, STOC’07—Proceedings of the 39th Annual ACM Symposium on Theory of Computing, 57–66, ACM, New York, 2007.
Pdf del artículo.
[11] Harvey, D. y J. van der Hoeven, Faster Integer multiplication using short lattice vectors. febrero 2018, arXiv:1802.07932.


Dejar una contestacion