Ya hemos discutido en estas páginas que las Matemáticas son el lenguaje del Universo así como del papel esencial que juegan en el método científico. En esta entrada vamos a ver con algo más de detalle esta última parte. Para ello discutiremos que es una teoría física y veremos un par de ejemplos representativos. Ante todo hemos de decir que la Física es la Ciencia que estudia la Naturaleza y que para ello se basa en medidas y observaciones experimentales de la realidad que nos rodea, es decir, en cuantificar o caracterizar los distintos fenómenos naturales mediante expresiones cuantitativas o números y a partir de ellos proponer teorías que los expliquen.
Las propiedades medibles u observables que se consideran en la Física se denominan magnitudes físicas: por ejemplo la longitud, la velocidad, la energía, etc. El objeto o conjunto de objetos a estudiar se denomina sistema físico: por ejemplo una partícula material, un átomo, un coche, etc. Cuando conocemos las medidas de un sistema que lo caracterizan biunívocamente decimos que el sistema se encuentra en un estado determinado.
Así pues, los objetivos de toda teoría física son, en general, los siguientes:
1. Describir el estado del sistema físico, es decir, dar una representación cuantitativa (matemática) del estado que lo defina de forma única.
2. Conocer la dinámica del sistema, es decir dado un estado inicial en el momento \(t_0\) conocer su evolución temporal para \(t>t_0\).
3. Predecir los resultados de las mediciones de las magnitudes físicas del sistema.
Desde un punto de vista formal una teoría física está en general constituida por:
1. El formalismo: Conjunto de símbolos y reglas de deducción a partir de los cuales se pueden deducir proposiciones y enunciados. En general toda teoría comienza fijando un cierto número de axiomas comúnmente denominados postulados.
2. Ley dinámica: Cierta relación (o relaciones) entre algunos de los principales objetos del formalismo que permitan predecir acontecimientos futuros.
Hasta aquí el avispado lector descubrirá que apenas hay diferencia entre una teoría matemática y una física. La principal diferencia reside en lo siguiente:
3. Interpretación física: Conjunto de reglas que permiten asignar valores experimentales a algunos de los símbolos del formalismo.
Es lo que algunos llamamos “el método de reducción al absurdo de la Naturaleza” o “poniendo los pies en la Tierra”. Es este tercer punto el que hace funcionar el método científico ya que gracias a él sabremos si una teoría va a poder explicar o no los fenómenos que se pretenden entender y describir usando las técnicas descritas en los puntos 1 y 2. Una teoría matemática tiene vida propia, se rige por sus propias leyes, muchas veces estéticas, no así una teoría física que tiene que pasar el filtro de su utilidad a la hora de describir los fenómenos naturales.
Como ejemplo ilustrativo elegiremos la mecánica newtoniana de una partícula material que se mueve en una dimensión. Imaginemos que tenemos una partícula de masa \(m\) que se mueve en una única dirección bajo la acción de cierta fuerza \(F\) (si quiere, puede pensar el lector en una canica de acero que rueda por un carril en el suelo) tal y como se muestra en la siguiente figura:

El estado de nuestra partícula vendrá determinado por la posición y la velocidad de la misma. Las distintas magnitudes que podemos medir en cada instante de tiempo son, entre otras, la posición de la bola \(x(t)\) en cada instante de tiempo \(t\), su velocidad \(v(t)\), la aceleración \(a(t)\), la energía cinética \(T=\frac12 m v^2(t)\), etc. Antes de continuar conviene hacer un breve paréntesis para explicar qué son algunas de las magnitudes antes mencionadas.
Según el Diccionario de la Lengua Española (DLE) la velocidad es una magnitud física que expresa el espacio recorrido por un móvil en la unidad de tiempo. Así mismo, la aceleración es una magnitud que expresa la variación de la velocidad en la unidad de tiempo. Si queremos expresar esta variación en términos matemáticos necesitamos uno de los conceptos más importantes de las matemáticas: el concepto de derivada de una función. Para definir la derivada podemos otra vez acudir al DLE que dice que la derivada es el valor límite de la relación entre el incremento del valor de una función y el incremento de la variable independiente, cuando este tiende a cero. Así pues, si \(x(t)\) representa la distancia recorrida por nuestra partícula tendremos que la velocidad es
\(v(t)=\displaystyle\lim_{\Delta t\to0}\frac{x(t+\Delta t)-x(t)}{\Delta t}\)
y la aceleración sería la derivada de la velocidad, es decir la segunda derivada de la posición. El concepto de derivada tiene una larga e interesante historia desde que fue introducido en las matemáticas independientemente por Newton y Leibniz en el siglo XVII al desarrollar ambos lo que hoy día conocemos como el Cálculo diferencial e integral, pero esto es otra historia.
Continuemos ahora con nuestro ejemplo. Lo segundo que debemos tener en nuestra teoría física es una ley dinámica, que en este caso no es más que la 2ª Ley de Newton. Dicha ley establece que \(F=m\cdot a\) donde \(a\) es la aceleración de la partícula, o sea, la aceleración de una partícula es proporcional a la fuerza aplicada e inversamente proporcional a la masa de la misma. Si denotamos por \(x(t)\) la posición de nuestra partícula entonces la segunda Ley de Newton toma la forma \(F(t)=m \ddot{x}(t)\) que es una ecuación diferencial (ya que su incógnita no es una cantidad algebraica sino una función, en este caso el desplazamiento de nuestra partícula). Aquí hemos usado la notación que usó Newton para las derivadas: \(v(t)=\dot{x}(t)\), \(a(t)=\dot{v}(t)=\ddot{x}(t)\) , que es la usual en muchos textos de Física, no así en los de Matemáticas donde es más usual la notación de Leibniz. Para resolver la ecuación diferencial obtenida (algo que en muchas ocasiones es complicado y que no es el objetivo de esta entrada) debemos conocer los valores de \(x(t)\) y su derivada \(\dot{x}(t)=v(t)\) en cierto instante de tiempo \(t_0\), es decir, las denominadas condiciones iniciales del problema (en nuestro ejemplo, la posición y velocidad inicial de nuestra partícula) que denotaremos por \(x_0=x(t_0)\) y \(v_0=v(t_0)=\dot{x}(t_0)\), respectivamente.
Veamos ahora dos casos particulares muy sencillos. El primero de ellos es cuando la fuerza es una fuerza constante. Entonces nuestra ecuación diferencial se convierte en \(\ddot{x}(t)=F/m=a\). Usando las reglas del Cálculo (que no vamos a explicar aquí) se deduce que \(v(t)=\dot{x}(t)=v(t_0)+a t\) y \(x(t)= x(t_0)+v(t_0)t+a t^2/2\). Es decir, si sobre el cuerpo actúa una fuerza constante el espacio que recorre depende de forma cuadrática del tiempo. De la fórmula anterior se deduce, en particular, que si \(F=0\), entonces \(a=0\), y por tanto \(v(t)=v(t_0)\) o sea, el cuerpo se mueve con velocidad constante, tal y como estableció Galileo años antes (y que es, a su vez, la primera de las tres Leyes de Newton de la Mecánica).
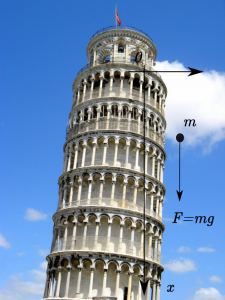
Consideremos ahora el problema de un cuerpo que cae desde cierta altura. Supongamos, por ejemplo, que dejamos caer nuestra bola de acero desde la torre de Pisa (como dice la leyenda que hizo Galileo en su día). Dado que la fuerza que actúa sobre la bola es la fuerza de la gravedad que es igual a \(F=m\cdot g\), donde \(m\) es la masa y \(g\) es una constante, usualmente denominada aceleración de la gravedad, entonces, utilizando nuevamente la segunda Ley de Newton obtenemos que \(a=g\).
Suponiendo que dejamos caer nuestra bola desde el reposo, o sea \(v_0=0\), deducimos que la distancia \(x(t)\) que recorre la bola se escribe mediante la fórmula \(x(t)=g\cdot t^2/2\), o sea la distancia recorrida es proporcional al cuadrado del tiempo transcurrido. Esta relación fue precisamente la Ley que describió Galileo en su obra Discurso y demostraciones matemáticas, en torno a dos nuevas ciencias, concretamente en el Teorema II, Proposición II del capítulo Sobre el movimiento naturalmente acelerado Galileo prueba que «Si un móvil cae, partiendo del reposo, con un movimiento uniformemente acelerado, los espacios por él recorridos en cualquier tiempo que sea están entre sí como el cuadrado de la proporción entre los tiempos, o lo que es lo mismo, como los cuadrados de los tiempos.»
El segundo ejemplo que vamos a considerar es el del sistema físico conocido como oscilador armónico. Un ejemplo de este tipo de sistemas es el compuesto por una partícula de masa \(m\) (nuestra canica de acero por ejemplo) sujeta a la pared por un resorte o muelle. En la siguiente figura se muestra un esquema simplificado de un oscilador armónico:
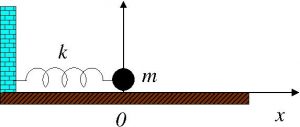
Si estiramos el resorte este aplica a la bola una fuerza proporcional (y en sentido contrario) a la elongación (o deformación) del mismo. Supongamos que el punto marcado con \(0\) en el esquema representa la posición de equilibro (es decir, cuando el resorte no está ni estirado ni comprimido), y denotemos por \(x(t)\) la elongación del muelle. Entonces, sobre la bola siempre actúa una fuerza proporcional a la elongación cuya expresión es \(F=- k \cdot x(t)\) siendo \(k\) cierta constante conocida como constante elástica del muelle (el signo menos se debe a que la fuerza siempre se opone al movimiento de muestra bola como bien puede comprobar el lector si intenta estirar o comprimir un muelle). Por tanto, la ecuación del movimiento es, según la segunda Ley de Newton, \(m \ddot{x}(t) = – k \cdot x(t)\), o equivalentemente, \(\ddot{x}(t) + \omega^2 \cdot x(t)=0\), donde \(\omega^2=k/m\). La solución general de esta ecuación es una función sinusoidal de la forma \(x(t)=A\sin(\omega t+\delta)\). Dicha función representa las oscilaciones de la partícula alrededor de la posición de equilibrio \(0\), donde \(A\) es la amplitud y \(\omega\) es la frecuencia de la oscilación. En la siguiente figura vemos una representación gráfica de dicha función donde se muestra además del periodo de la oscilación \(T=2\pi/\omega\), la propia amplitud de la misma:

En la siguiente figura animada mostramos una representación de lo que le ocurre a nuestra bola de acero. Por sencillez hemos escogido el caso cuando alargamos el muelle hasta una distancia \(A\) del punto de equilibro y luego lo soltamos de forma que su velocidad inicial sea cero.
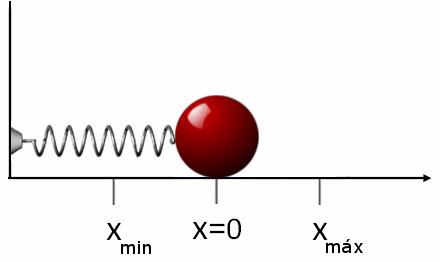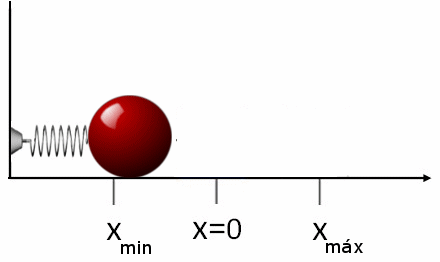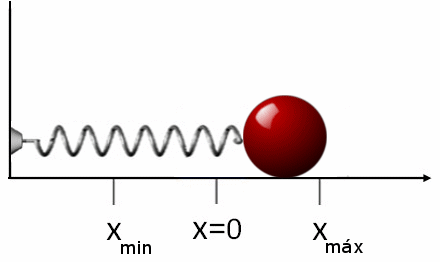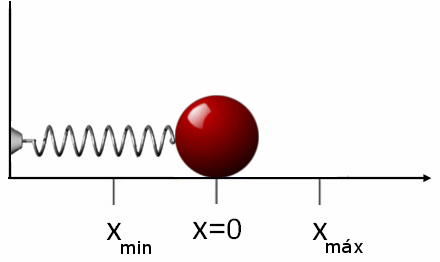
Como podemos comprobar la bola oscila entre los valores \(x_{min}=-A\) y \(x_{max}=A\), puntos estos donde se detiene la bola y cambia el sentido de su movimiento. En estos dos puntos la elongación \(x(t)\) es la más grande posible (en valor absoluto) e igual a \(A\) mientras que su velocidad es cero. Por el contrario en la posición de equilibrio \(x(t)=0\) la bola tiene la mayor velocidad (en valor absoluto) posible igual a \(\omega A\).
Para el caso del oscilador armónico vamos a calcular la energía total de la partícula. Para ello usaremos la fórmula
\(E=\frac{m\cdot v(t)^2}2+\frac{k\cdot x(t)^2}2.\)
Si sustituimos en dicha expresión la solución que encontramos antes obtenemos para la energía total de nuestro oscilador el siguiente valor: \(E=\frac{ k A^2}2\). Nótese que este valor no depende del tiempo así que estamos en presencia de un sistema donde se conserva la energía.
Aunque muy sencillos, estos ejemplos muestran muy bien como se construye una teoría física. Hemos de mencionar que una característica importante del oscilador armónico que se deduce de las fórmulas anteriores es que su energía, que ya hemos visto que se conserva a lo largo de tiempo, es una función que varia de forma continua con la amplitud de la oscilación (esta última sólo depende de los valores iniciales de la \(x(t)\) y \(v(t)\)). Esta es una propiedad de casi todos los sistemas macroscópicos conocidos. Fue toda una sorpresa cuando se descubrió que muchísimos sistemas microscópicos (como átomos y moléculas, por poner un ejemplo) la energía dejaba de ser continua y se convertía en una función a saltos. Pero esta es la historia de la Mecánica Cuántica que discutiremos en otra ocasión.
Así pues, vemos que las matemáticas juegan un papel esencial en la construcción de toda teoría física, de hecho son una parte esencial de la misma ya que sin matemáticas no hay teoría física propiamente dicha. Pero su relación es mucho más profunda. Una muy buena descripción de ello es la que realizó el gran matemático soviético Vladimir I. Arnold quien en su magnífico ensayo Sobre la enseñanza de las Matemáticas escribió «Desde mediados del siglo XX se ha tratado de dividir la física y la matemática. Las consecuencias han sido catastróficas. Generaciones enteras de matemáticos han crecido sin conocer la mitad de su ciencia y, por supuesto, en total ignorancia de las otras ciencias […] la matemática sin la física no es apta para la enseñanza ni para su aplicación en cualquier otra ciencia.»

Dejar una contestacion