Los analemas
Un analema terrestre es, por definición, la curva que describe la posición del Sol en el cielo si todos los días del año se lo observa a la misma hora (tiempo oficial) y desde el mismo punto de la Tierra. Su aspecto es muy similar al de una lemniscata. El término analema proviene del griego y etimológicamente significa «pedestal de un reloj de sol» (por razones que se verán más adelante).
De igual forma puede hablarse de analemas asociados a los otros planetas del Sistema Solar. No obstante, su aspecto puede ser muy diferente. Por ejemplo, en Marte, los analemas son curvas similares al perfil de una gota de agua.
Un analema se consigue colocando una cámara fotográfica en un lugar fijo, apuntando a una posición del cielo por donde pase el Sol (a ser posible, un punto de la eclíptica), de manera que produzca una foto cada día, siempre a la misma hora. La superposición de todas las imágenes obtenidas a lo largo del año proporciona la curva deseada.
Otro método consiste en clavar una estaca en el suelo y marcar la posición del extremo de la sombra cada día, siempre a la misma hora, a lo largo de un año. De este modo se construyen los relojes solares.
El tiempo solar, el tiempo oficial y la ecuación del tiempo
Los analemas existen por dos motivos: porque la velocidad del movimiento de traslación de la Tierra alrededor del Sol no es constante (de acuerdo con las leyes de Kepler) y porque el eje de rotación de la Tierra es oblicuo y no ortogonal al plano de su órbita (la oblicuidad oscila entre 21.55 y 24.18 grados).
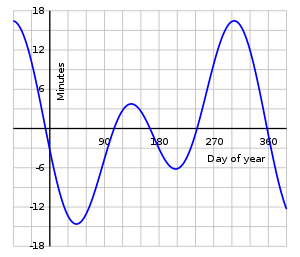
Esto genera en cada instante de tiempo \(t\) una diferencia considerable entre el tiempo solar y el tiempo oficial, \(E(t)\), que puede calcularse de manera muy aproximada de acuerdo con la expresión
$$
E(t)=a_1 \sin (b_1 + c_1 t) + a_2 \sin (b_2 + c_2 t),
$$
donde las \(a_i\), \(b_i\) y \(c_i\) son constantes positivas. Para el año 2016, los valores correctos (con \(t\) medido en días a partir del 1 de enero y los ángulos en grados) fueron \(a_1=595\), \(a_2=442\), \(b_1=198\), \(b_2=175\), \(c_1=1.9713\) y \(c_2=0.9856\).
Los valores de \(E(t)\) pueden llegar al orden de 16 minutos en ciertas épocas del año. Esta diferencia también conduce a falta de simetría en las horas de salida y puesta del Sol.
La declinación solar
La declinación solar es el ángulo que forma la recta Tierra-Sol con el plano del Ecuador celeste. Se trata de una de las dos coordenadas del sistema Tierra-Sol de representación ecuatorial; la otra coordenada se denomina ascensión recta.
De igual manera puede definirse la declinación de cualquier objeto astral. Así, un objeto en el Ecuador celeste (resp. sobre el Polo Norte o Polo Sur) tiene una declinación de \(0°\) (resp. \(90º\) o \(-90º\)).
En latitudes altas (\(>67º\)) es posible que durante una parte del año el Sol tenga una declinación mayor que \(90-67=23º\) y, por tanto, esté siempre sobre el horizonte (el Sol de medianoche).
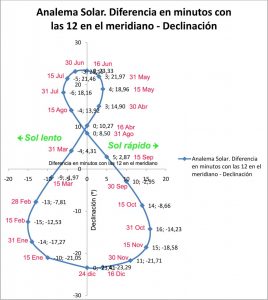La declinación solar se mide en grados y su valor está dado por
$$
D(t) = -a_3 \cos(b_3 + c_3 t),
$$
donde (de nuevo) \(a_3\), \(b_3\) y \(c_3\) son constantes positivas. Para el año 2016, los valores son \(a_3=23.44\), \(b_3=9.836\), \(c_3=0.9836\).
Si se interpreta y se representa \((E,D)\) como una curva plana parametrizada por \(t\), se obtiene el analema solar.
La lemniscata
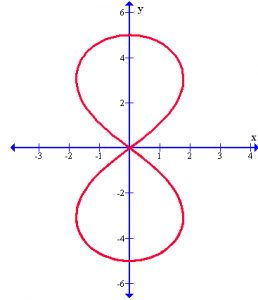
El analema es una curva parecida (pero no totalmente coincidente) con la lemniscata. Ésta última es la curva plana de ecuación
$$
(x^2+y^2)^2 = 2k^2 (y^2-x^2)
$$
(\(k\) es una constante). Se trata del lugar geométrico de los puntos tales que el producto de sus distancias a dos puntos fijos (los puntos \((0,-k)\) y \((0,k)\)) es constante. Se puede obtener fácilmente resolviendo la ecuación diferencial
$$
x(x^2 + y^2 – k^2)\,dx = -y(x^2 + y^2 + k^2)\,dy.
$$
Fue descubierta y denominada así por Jakob Bernouilli (del latín «lemniscus», cinta colgante). Desde 1655, gracias a J. Wallis, se utiliza como símbolo del infinito.
Para saber más:
- Stuart Bennett, «A History of Control Engineering, 1930-1955», Peter Peregrinus Ltd., London, 1993.
- https://sudandolagotagorda.blogspot.com.es/2009/10/hora-solar-hora-legal-i.html
- https://sudandolagotagorda.blogspot.com.es/2010/07/trazando-el-analema.html
- https://matematiquemos.blogspot.com.es/2014/09/la-lemniscata-de-bernoulli.html
Creo que debemos preguntarnos qué ubicación tiene la Tierra en el sistema solar para que la curva tenga ese comportamiento. Y con ello predecir, que en otro sistema solar, un planeta posicionado como la Tierra también debería mostrar en su analema una lemniscata.