Solución: Fórmula olvidada

Publicamos la solución al divertimento Fórmula olvidada. Gracias a Cristóbal Sánchez-Rubio, Daniel Gómez y Alberto Castaño por las soluciones que han propuesto.

Divertimento:

A un alumno (masculino genérico) que hace un examen sobre las aplicaciones de la Trigonometría, le piden el área de un trapecio del que se conocen las dos bases \(B\) y \(b\), que son dos números enteros, y los ángulos que forman los lados no paralelos con la base mayor, 30º y 60º respectivamente. El estudiante calcula la altura \(h\) del trapecio, pero no recuerda la fórmula del área del mismo (que no está en el tema del que se examina) y no sabe cómo se deduce esa fórmula; duda entre

$$ S_1=\frac{B+b}{2}\cdot h \qquad \text{y} \qquad S_2= \frac{B\cdot b}{2} + h.$$

Calcula ambos valores con los datos que tiene y obtiene el mismo resultado con lo que opta por escribir en el examen tras el cálculo de la altura

Por tanto, el área del trapecio es …

sin detallar la fórmula que ha utilizado.

Se pide saber si el alumno se equivocó al obtener el mismo valor por la aplicación de ambas fórmulas o, en caso contrario, la relación que existe entre las longitudes de las bases para que dicha igualdad suceda.

Solución:

Solución propuesta por Cristóbal Sánchez-Rubio.

Es evidente que la segunda fórmula no es un área, queda averiguar si para algún valor de las medidas puede dar el mismo resultado. Los triángulos ADD’ y CC’B son semejantes y ambos del tipo \(30^o-60^o-90^o\). Por tanto, es claro que $$AD’=\frac{h}{\sqrt{3}}, \quad C’B=h \sqrt{3},$$

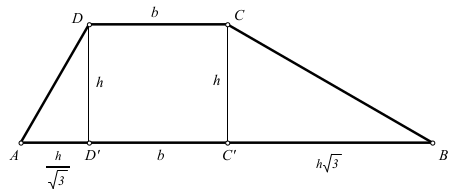
como se muestra en la figura. Además

$$B-b= h \Big( \frac{1}{\sqrt{3}} + \sqrt{3} \Big) = \frac{4}{3}h\sqrt{3},$$

de donde

$$h=\frac{\sqrt{3}(B-b)}{4}.$$

Si las dos fórmulas arrojasen un mismo valor, debería ser

$$ \frac{(B+b)}{2} \frac{\sqrt{3}(B-b)}{4} = \frac{B \cdot b}{2} + \frac{\sqrt{3}(B-b)}{4},$$

despejando \(\sqrt{3}\) resulta

$$ \sqrt{3}=\frac{4Bb}{(B-b)(B+b-2)}.$$

Imposible ya que al ser las bases enteras el miembro de la derecha es racional y \(\sqrt{3}\) es irracional. Por tanto el alumno del que habla el enunciado se equivocó al obtener el mismo valor por la aplicación de ambas fórmulas.