En varias entradas anteriores hemos comentado que las Matemáticas son el lenguaje de la naturaleza (ver aquí) y también hemos visto que juegan un papel fundamental en el método científico (ver aquí). Qué existe una estrecha relación entre la Matemática y el mundo que nos rodea, ese aparente misterio del que hablaban Einstein y Wigner, también lo discutimos en esta otra entrada. Esta relación de las matemáticas y el mundo que nos rodea también la describe de forma magistral el genial matemático John Von Neumann (1903-1957) en su artículo The Mathematician (El matemático) publicado en 1947 donde afirma:
Creo que es una aproximación relativamente buena a la verdad -que es demasiado complicada para permitir cualquier cosa menos aproximaciones- que las ideas matemáticas se originan en lo empírico, aunque la genealogía es a veces larga y oscura. Pero una vez concebidas, estas comienzan a vivir una vida peculiar propia, gobernadas por motivaciones casi totalmente estéticas, y es mejor compararlas a lo creativo que con cualquier otra cosa y, en particular, con una ciencia empírica.
En esta entrada queremos mostrar uno de los ejemplos más representativos de lo que dice Von Neumann, concretamente mostraremos como una teoría matemática nacida de la Física puede cobrar vida propia y dar lugar a estudios matemáticos no sólo interesantes, sino que han cambiado las propias Matemáticas. Nuestro ejemplo está relacionado con las denominadas series trigonométricas usualmente llamadas series de Fourier.
Una serie trigonométrica es una serie infinita del tipo
\(\displaystyle S=\displaystyle\frac{a_0}2+\sum_{n=1}^\infty a_n \cos (n x)+b_n \sin (n x),\)
donde \(a_n\) y \(b_n\) son ciertas sucesiones numéricas dadas de antemano. Por ejemplo
\(\displaystyle\sin(x)+\frac{\sin 3x}{3}+ \frac{\sin 5x}{5}+ \frac{\sin 7x}{7}+\cdots\)
Históricamente, las series trigonométricas como la anterior aparecieron en el siglo XVIII al intentar resolver ciertos problemas físicos relacionados con las vibraciones de una cuerda. Este vídeo muestra muy bien dichas vibraciones.
Este problema lo trató por primera vez con cierto detalle Jean Bernoulli (en 1727), y más adelante su hijo Daniel Bernoulli (en 1733). También fue considerado por Leonard Euler (en 1736), aunque no es hasta el trabajo de Jean d’Alembert de 1746 (publicado en 1749) que se consigue un avance significativo.

d’Alembert, a partir de las ecuaciones de Newton de la mecánica, dedujo la que hoy conocemos como ecuación de ondas
\(\displaystyle\frac{\partial^2 y(x,t)}{\partial t^2}=v^2 \frac{\partial^2 y(x,t)}{\partial x^2},\)
donde \(v\) es cierta constante (la velocidad de propagación de la onda). También d’Alembert encontró que la solución de la ecuación de ondas se podía escribir de la forma \(y(x,y)=\phi(x+vt)+\psi(x-vt)\), donde \(\phi\) y \(\psi\) son funciones cualesquiera con tal de que tengan derivadas parciales de orden dos. En particular probó si la cuerda está fija en sus extremos y tiene longitud \(l\) y en el instante inicial tiene la forma definida por cierta función \(f(x)\) entonces la solución más general tenía la forma
\(y(x,t)=\frac12 \phi(x+vt)-\frac12 \phi(vt-x),\)
donde \(\phi\) es una función dos veces diferenciable (o sea tiene dos derivadas), periódica con período \(2l\) e impar y además ha de ser tal que en \([0,l]\) \(\phi(x)=f(x)\). A la expresión anterior llegaron tanto el propio d’Alembert como Euler (que publicó un artículo sobre el tema en 1948 poco después de leer el trabajo de d’Alembert), siendo para este último la solución definitiva del problema de la cuerda vibrante.
Sobre esta última afirmación se generó cierta polémica, pues Daniel Bernoulli en un artículo de 1753 (publicado en 1755) defendió mediante argumentos físicos que la solución general no era la fórmula de d’Alembert y Euler sino la serie infinita
\(\displaystyle y(x,t)=\sum_{m=1}^\infty c_m \sin\frac{m\pi x}{l} \sin\frac{m\pi at}{l}.\)
Nótese que de la fórmula anterior se deduce, en particular, que si \(t=0\), entonces
\(\displaystyle y(x,0)=f(x)=\sum_{n=1}^\infty c_n \sin\frac{n\pi x}{l}\),
es decir, la función \(f(x)\) (que a priori es arbitraria), ha de poder representarse, al menos en el el intervalo \([0,l]\), como una serie trigonométrica. Esta propiedad no es nada trivial de demostrar y la búsqueda de la
respuesta a la misma generó una cantidad ingente de problemas y teorías matemáticas interesantes, algunas de las cuales mencionaremos en breve.
Volviendo al trabajo de Bernoulli, este argumentaba que como en su fórmula disponía de infinitos coeficientes \(c_n\) esto le permitiría sin problemas poder representar cualquier función, aunque no tenía ningún método para hacerlo (en el caso de una suma infinita). Hoy día es obvio que eso no es cierto en general pues el número infinito de coeficientes de que disponía Bernoulli no es comparable con el número de puntos donde esta definida la función: uno es numerable o contable (el número de los coeficientes \(c_n\)) mientras que el otro, el número de puntos de \(f\) en el intervalo \([0,l]\) no lo es, pero para eso habría que esperar a Cantor y sus estudios sobre la teoría de conjuntos y los números transfinitos, teoría que estuvo motivada precisamente por el problema de la unicidad de la representación de una función mediante una serie de Fourier (de la cual la serie de Bernoulli es un caso particular).
Antes de continuar conviene hacer notar que si tenemos un desarrollo como el anterior podemos, formalmente, multiplicar ambos miembros de la ecuación por \(\sin\frac{k\pi x}{l}\), e integrar de \(0\) a \(l\). Si usamos que
\(\displaystyle \int_0^l \sin\frac{k\pi x}{l} \sin\frac{m\pi x}{l}dx=0, \mbox{ si } m\neq k,\, m=0\, \mbox{ ó } k=0, \mbox{e igual a }\,\frac{l}2, \mbox{ si } m=k,\)
obtenemos el siguiente valor para los coeficientes \(c_n\)
\(\displaystyle c_n=\frac{2}l \int_{0}^l f(s) \sin\frac{n \pi s}{l} ds.\)
De este hecho (esencialmente) se dio cuenta Euler en 1777 aunque el resultado fue publicado después de su muerte en 1793.
El siguiente paso relevante de esta historia se debe a Joseph Fourier. Fourier estaba interesado en uno de los problemas más interesantes de principios del siglo XIX: la transmisión del calor por un cuerpo. Aunque el primer primer trabajo de Fourier lo presentó en 1807 no es hasta 1822 que se publica su obra fundamental y que ha sido sin duda uno de los más influyentes tratados matemáticos de la historia: Théorie analytique de la chaleur (Teoría analítica del calor).

Basándose en principios físicos Fourier dedujo lo que es hoy otra de las ecuaciones fundamentales de la física-matemática: la ecuación del calor. Si nos restringimos a una única dimensión la ecuación que describe la propagación del calor en una barra homogénea de longitud \(l\) tiene la forma
\(\displaystyle \frac{\partial u(x,t)}{\partial t}=a^2 \frac{\partial^2 u(x,t)}{\partial x^2},\)
donde \(u(x,t)\) es la temperatura de la barra en el punto \(x\) y en tiempo \(t\). A la ecuación anterior habrá que agregarle una condición inicial (distribución de la temperatura) \(u(x,0)=f(x)\) y sendas condiciones de contorno \(u(0,t)=g_1(t)\) y \(u(l,t)=g_2(t)\), que por simplicidad tomaremos igual a cero.
Para resolver la ecuación del calor Fourier utilizó el método de separación de variables que introdujo d’Alembert en su estudio de la ecuación de ondas. La idea es suponer que la solución admite una representación en forma de variables separadas \(u(x,t)=X(x)T(t),\qquad X(x)\not\equiv0,\quad T(t)\not\equiv0.\)
Sustituyendo lo anterior en la ecuación original y tras varios cálculos no muy complicados Fourier dedujo que la solución general de la ecuación del calor venía dada por la serie
\(\displaystyle u(x,t)=\sum_{n=1}^\infty b_n e^{-\frac{a^2\pi^2n^2 t}{l^2}} \sin \frac{n\pi x}l, \)
con \(b_n\) ciertos números que hay que determinar.
Nótese que si \(t=0\) entonces, la condición inicial nos da a la fórmula
\(\displaystyle f(x)=\sum_{n=1}^\infty b_ n \sin \frac{n\pi x}l,\)
que es el desarrollo en senos de una función.
Es decir, otra vez volvemos a encontrarnos con el problema del desarrollo de una función en serie trigonométrica que ya hemos comentado antes. Aquí sin embargo Fourier usa un ingenioso método para encontrar la forma de los coeficientes que le conduce a la expresión
\(\displaystyle b_n=\frac{2}l \int_{0}^l f(s) \sin\frac{n \pi s}{l} ds\).
Aunque la forma en que dedujo Fourier la representación integral anterior para los coeficientes \(b_n\) dejaba mucho que desear desde el punto de vista del rigor, Fourier, a diferencia de sus antecesores, se dio cuenta de la importancia (y generalidad) de la misma. Por ejemplo, Fourier argumentó que bastaba que la curva \(f(x)\sin \frac{n\pi x}l\) tuviese área, lo cual tenía sentido según él para una gran cantidad de funciones que no tenían que ser ni siquiera continuas, incluso podrían no tener ni siquiera una representación analítica (es decir una única fórmula). De ello Fourier concluyó que cualquier función en \([0,l]\) admitía una representación en series de senos. Pero fue más allá, pues a partir de diversos ejemplos concretos afirmó que la representación era siempre válida en \([0,l]\) sin que importase lo que pasara fuera de dicho intervalo. Además defendió que dos funciones podían perfectamente ser idénticas en un intervalo determinado, y distintas fuera del mismo. Este hecho fue de vital importancia pues muchos matemáticos de la época no consideraban factible esta posibilidad.
En defensa de dichos matemáticos debemos mencionar que todavía en la época de Fourier no estaba claro el concepto de función. De hecho existían distintas formas de entender lo que era una función siendo la más extendida la noción de que una función venía expresada por una única fórmula. Fue Euler uno de los primeros en defender que una función podía venir descrita por varias fórmulas, es lo que hoy llamamos una función definida a trozos, como la de la siguiente figura:
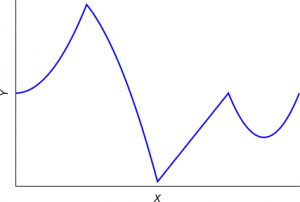
El trabajo de Fourier fue esencial en la clarificación del concepto de función. Era impensable antes del trabajo de Fourier que una función pudiese ser como la que hoy día conocemos como función de Dirichlet que tomaba valores iguales a 1 en todos los puntos racionales de la recta real y 0 en los irracionales y que aparte de no ser continua en ningún punto es imposible de representar gráficamente.

De hecho a Peter Gustav Lejeune Dirichlet se le atribuye la definición moderna de función:
Una función es una regla de forma que a cada valor \(x\) de un conjunto (numérico) se le hace corresponder (no importa cómo) el valor \(y\), en cuyo caso se dice que \(y\) es una función de \(x\) y se escribe como \(y(x)\).
Pero regresemos al trabajo de Fourier. Tras considerar los desarrollos de funciones en senos Fourier analiza desarrollos en cosenos para, a continuación, estudiar la representación de una función en el intervalo \([-l,l]\). Tras el análisis de distintos ejemplos deduce que cualquier función se puede representas en \([-l,l]\) por la serie
\(\displaystyle f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n \cos\frac{n\pi x}{l}+b_n \sin\frac{n\pi x}{l},\)
donde
\(\displaystyle a_n= \frac1{l} \int_{-l}^l f(x) \cos {\frac{n\pi x}{l}} dx,\quad b_n= \frac1{l} \int_{-l}^l f(x)\sin{\frac{n\pi x}{l}} dx, \quad n=0,1,2,3,\dots\,.\)
El desarrollo anterior es precisamente el que conocemos hoy día como serie de Fourier y que representa funciones en el intervalo \([-l,l]\) y a sus extensiones periódicas fuera de dicho intervalo.
Nótese que para que tenga sentido las expresiones anteriores las integrales que definen los coeficientes \(a_n\) y \(b_n\) han de estar bien definidas. De hecho para poder responder a la pregunta de qué funciones admiten una serie de Fourier se tuvo que desarrollar una teoría rigurosa de la integración, primero a manos de Bernhard Riemann hasta llegar a la teoría de integración de Henri Lebesgue.
Si ahora asumimos que dada una función \(f\), existe su serie de Fourier, entonces surge de manera natural la pregunta de si realmente la serie de Fourier representa a la función \(f\) de partida. Antes de responder a esa pregunta conviene mostrar unos ejemplos sencillos:
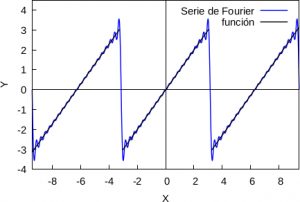
Ejemplo 1: Sea la función \(f(x)=x\) definida en \((-\pi,\pi]\) y extendámosla periódicamente a todo el eje real. El desarrollo de Fourier de la misma es:
\(\displaystyle S_f(x)=2\sum_{k=0}^\infty \frac{(-1)^{k+1}\sin kx}{k}.\)
En la figura siguiente podemos ver una representación de los primeros 10 sumandos de la misma. Nótese que \(f\) es discontinua en los puntos \((2k+1)\pi\), \(k=0,\pm1,\pm2,\ldots\) mientras que las sumas parciales de \(S_f\) son continuas y además \(S_f((2k+1)\pi))=0\).
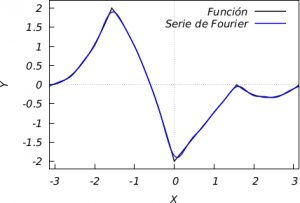
Ejemplo 2: Mostremos ahora un ejemplo de una función como la que proponía Euler. Sea \(g\) definida en \((-\pi,\pi]\) por
\(\displaystyle g(x)=\left\{\begin{array}{ll}\mbox{si}\; x\in[-\pi,\pi/2), \quad & f(x)={{8\,\left(x+ \pi\right)^2}\over{\pi^2}}, \\[3mm] \mbox{si}\; x\in[-\pi/2,0),\quad & f(x)={{5}\over{2}}-\frac12{\left({{4x+3 \pi}\over{\pi}}\right)^2}, \\[3mm] \mbox{si}\; x\in[0,-\pi/2),\quad & f(x)={{4\,\left(x+\pi\right)}\over{\pi}}-6, \\[3mm] \mbox{si}\; x\in[\pi/2,\pi),\quad & f(x)= \frac13{\left( {{4 x-3\pi}\over{\pi}}\right)^2}-\frac13. \\ \end{array} \right. \)
y extendámola periodicamente a todo el eje real. Tras laboriosos cálculos podemos obtener los primeros 10 términos de la serie que vemos en la siguiente figura:
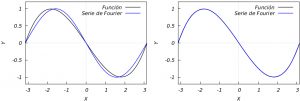
Ejemplo 3: Finalmente consideremos la función \(h(x)=x(x^2-\pi^2)\) en \([-\pi,\pi)\) cuya serie de Fourier es
\(\displaystyle S_f(x)=\sum_{k=1}^\infty \frac{(-1)^{k}\sin kx}{k^3}.\)
La gráfica muestra que incluso con un único sumando la aproximación es buena.
De los ejemplos anteriores se sigue que si la función es lo suficiente buena la convergencia de la serie parece mejorar notablemente así que surge la cuestión de si hay alguna relación entre la suavidad de \(f\) y la convergencia de su correspondiente serie de Fourier.
Uno de los primeros resultados rigurosos sobre este problema se debe a Dirichlet quien probó que: Si una función \(f(x)\) es una función periódica de periodo \(2l\), continua a trozos y acotada, que en un periodo tiene un número finito de máximos y mínimos locales y un número finito de discontinuidades, entonces la serie de Forier converge a \(f(x)\) en cada punto donde \(f\) es continua y al valor \(\displaystyle\frac{f(x+)+f(x-)}2 \) en los puntos de discontinuidad donde \(f(x+)\) y \(f(x-)\) son los límites por la derecha y por la izquierda}, respectivamente, es decir, los límites cuando \(h>0\) tales que \(\displaystyle f(x+)=\lim_{h\to0} f(x+h)\) y \(\displaystyle f(x-)=\lim_{h\to0} f(x-h)\), inaugurando así la búsqueda de condiciones suficientes que aseguraran la convergencia de la serie de Fourier.
Regresemos a la pregunta sobre qué condiciones debe satisfacer \(f\) para que tenga una serie de Fourier. El propio Dirichlet se dio cuenta que no para cualquier función la serie se podía definir. De hecho usó la función que lleva su nombre y que ya mencionamos antes para concluir que no para cualquier función las integrales van a estar definidas. Uno podría pensar que bastaría con que \(f\) fuese integrable (existiese la integral del valor absoluto de \(f\) ) según la definición de Lebesgue. La respuesta no se hizo esperar. Por un lado Andréi Kolmogorov probó en 1926 que existían funciones integrables cuya serie de Fourier divergían en todos los puntos y por otro Jean-Pierre Kahane y Yitzhak Katznelson en 1966 probaron que existían funciones continuas cuyas series de Fourier divergían en un conjunto suficientemente pequeño (denominado conjunto de medida nula). La respuesta más general conocida a día de hoy se debe al matemático sueco Lennart Carleson que probó en 1966 que si una función es de cuadrado integrable (es decir si \(|f(x)|^2\) es integrable), entonces se puede definir su serie de Fourier y esta converge a la función en casi todos los puntos del intervalo excepto quizá uno de medida nula. Lo anterior lo generalizó Richard Hunt en 1968 a funciones \(L^p\) con \(p>1\), i.e, cuando \(|f(x)|^p\) es integrable. Aunque con el Teorema de Carleson-Hunt el problema de la convergencia de las series de Fourier prácticamente queda resuelto todavía hay intentos de generalizarlos a espacios intermedios de funciones.
Como habrá comprobado el lector, para resolver el problema físico de cómo vibra una cuerda o cómo se trasmite el calor en un cuerpo fue necesario desarrollar una inmensa cantidad de áreas de las matemáticas, las cuales comenzaron a … vivir una vida peculiar propia, gobernadas por motivaciones casi totalmente estéticas, … tal y como decía Von Neumann en su artículo.
No puedo terminar esta entrada sin escribir como culmina Von Neumann la reflexión que trascribí al inicio de la misma. Von Neumann, continuaba su reflexión de esta manera:
Cuando una disciplina está durante una segunda y tercera generación inspirada sólo indirectamente por las ideas que proceden de la realidad, está amenazada por graves peligros. Se convierte cada vez más en el »arte por el arte». Esto no es necesariamente malo si la disciplina está bajo la influencia de hombres con un criterio extraordinariamente bien desarrollado. Pero existe un grave peligro de que la materia evolucione a lo largo de la línea de mínima resistencia. A gran distancia de su origen empírico, o después de muchas reproducciones «abstractas», un tema matemático está en peligro de degeneración.
Y ¿cuál es la solución que propone el bueno de Johnny?
Siempre que se alcance este punto, me parece que el único remedio es el retorno rejuvenecedor a la fuente, la reinyección de ideas más o menos directamente empíricas.
Es fácil deducir de las palabras de Von Neumann que esa aparente dependencia de la Matemática de la realidad, que asusta a tantos matemáticos, no es en lo absoluto degradante para la Matemática, ni debe ocultarse, sino más bien todo lo contrario: potenciarse.
Lecturas recomendadas:
F. Javier Duoandikoetxea Zuazo, 200 años de convergencia de las series de Fourier. Gaceta de la Real Sociedad Matematica Española, Vol. 10, No. 3 (2007), pp. 651-677.
Edward B. Van Vleck, The Influence of Fourier’s Series upon the Development of Mathematics. Science, New Series, Vol. 39, No. 995 (Jan. 23, 1914), pp. 113-124

Dejar una contestacion