El problema de Durero

Durero es conocido como pintor, pero no cabe duda de que en cierto sentido fue un matemático (véase la entrada Pacioli, Durero y la secretísima ciencia del cuerpo humano). Tanto que hoy en día todavía es un problema abierto confirmar alguna de sus observaciones. Presentamos hoy el problema de Durero.

El libro de Durero

Su obra matemática mas importante es Underweysung der Messung mit dem Zirckel und Richtscheyt (Instrucciones para medidas con regla y compás), tiene unas ilustraciones tan impresionantes que lo mejor que puede hacer el lector (y lo digo a pesar del peligro de perderlo) es dejar de leer esto y admirarlas por si mismo. Por ejemplo en el enlace: Rylands Collection encontrará una copia. Está escrito con letras góticas y en alemán pero eso no impedirá apreciar las ilustraciones. Existe una edición magnífica en inglés [1], con facsimil, que contiene copias de varias obras de Durero y que incluye una versión posterior del libro al que me he referido antes.

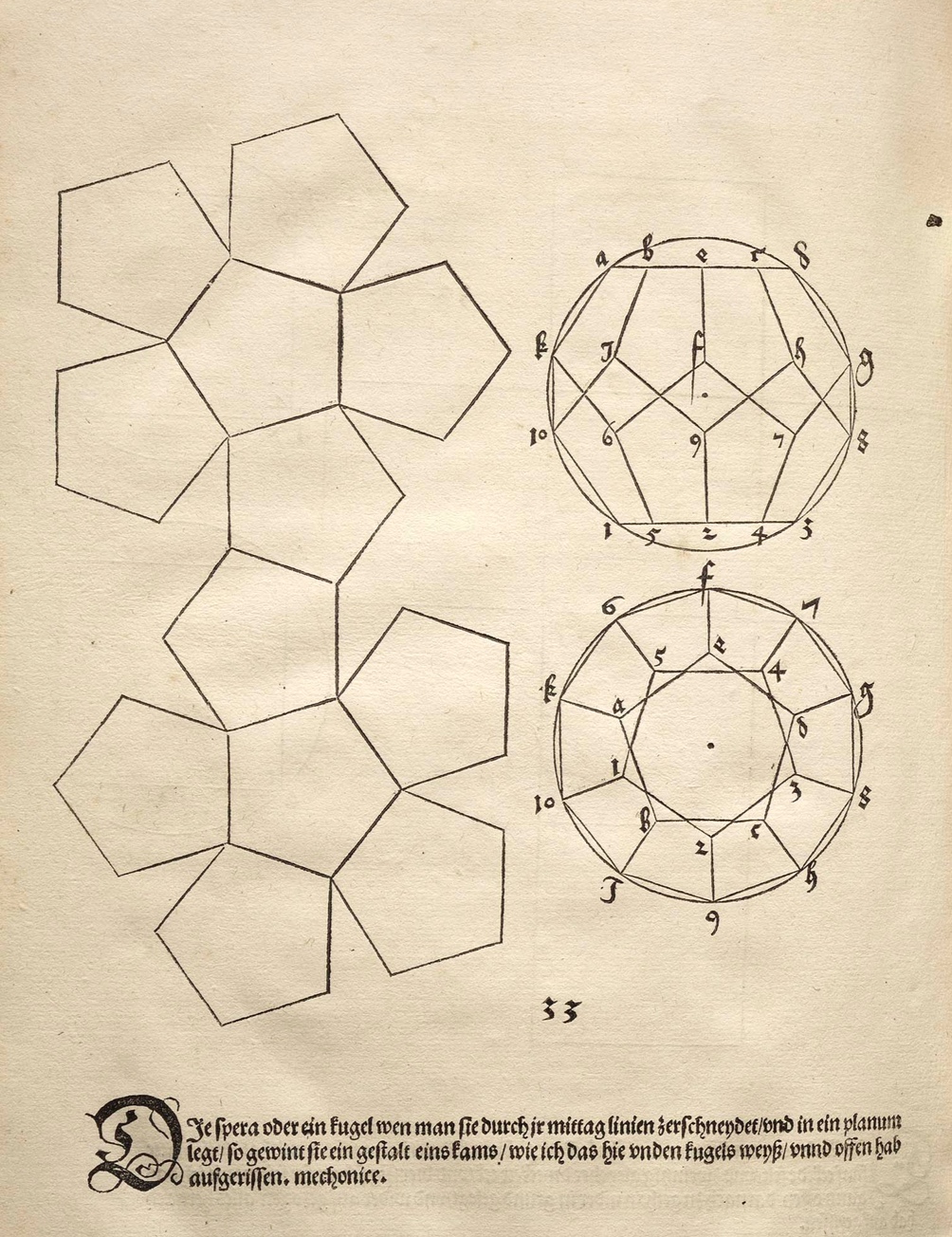
El cuarto capítulo del libro de Durero está dedicado a los poliedros. Un poliedro es una figura tridimensional. En forma tridimensional se representan el icosaedro y el dodecaedro en las ilustraciones del libro XIII de Euclides, pero Durero usa preferentemente un desarrollo plano de las caras del poliedro. ¿Quién no ha usado estos desarrollos para construir modelos tridimensionales de los poliedros regulares? Durero los necesita porque en su libro considera poliedros mas generales que los platónicos. En las figuras vemos las representaciones de Durero del dodecaedro y del icosaedro truncado, (que se ha popularizado por su uso en balones de futbol). Pero podemos imaginarlo cortando las esquinas de un icosaedro de manera que las caras triangulares se conviertan en hexágonos regulares y cada vértice da lugar a un pentágono regular.

 

Parece que la idea de usar estos desarrollos para la construcción de modelos viene de Durero.

¿Dónde está el problema? Hay que mirar esto con una mente muy matemática para darse cuenta de la cuestión. La mente fue la de Geoffrey Colin Shephard quién en 1975 formuló el problema:

Problema de Durero. ¿Admite todo poliedro convexo un desarrollo?

¿Como no? preguntará el lector. ¿Dónde está el problema? Quizás mirando la figura del cubo truncado (tomada de un libro de O’Rourke [2]) puedas hacerte una idea del problema.

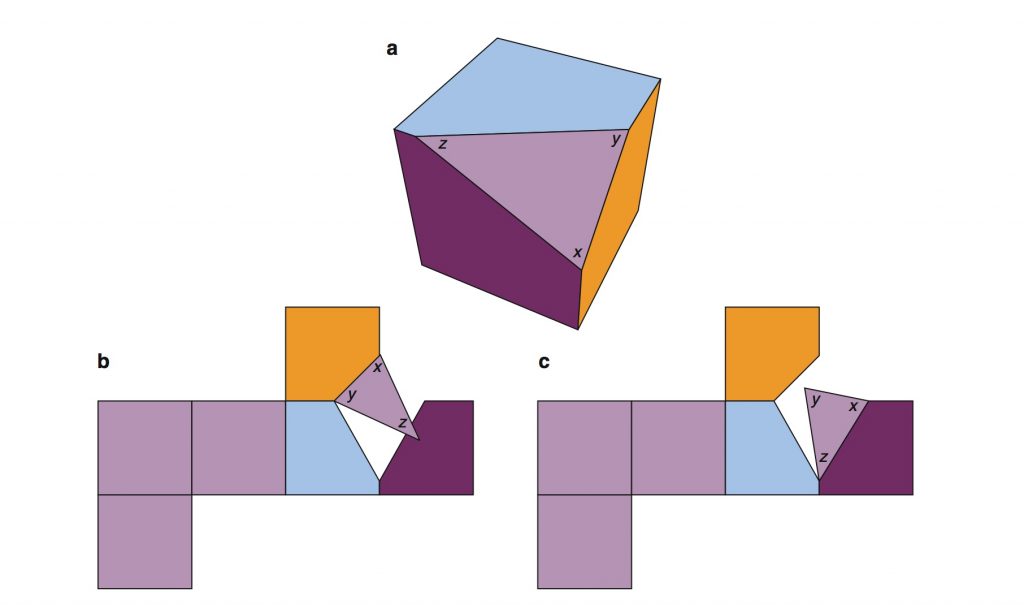
El cubo truncado admite el desarrollo (c) mostrado en la figura, pero (b) no podemos admitirlo como un desarrollo válido por el solapamiento de dos de sus caras.

Si miramos ahora al desarrollo de Durero del icosaedro truncado veremos que por poco es un desarrollo. Algunos pentágonos casi se superponen a algunos hexágonos.

La condición de que las caras no se solapen no es la única condición que se le impone a un desarrollo. Queremos que el desarrollo sea una figura conexa y que los cortes en el poliedro  se realicen a lo largo de sus aristas, esto es, el borde del desarrollo, debe provenir de aristas del poliedro cortadas para extender el poliedro.

Shephard [6] hace notar que para construir el poliedro a partir del desarrollo debemos indicar qué aristas han de pegarse para construirlo. Como ejemplo cita el desarrollo ambiguo siguiente:

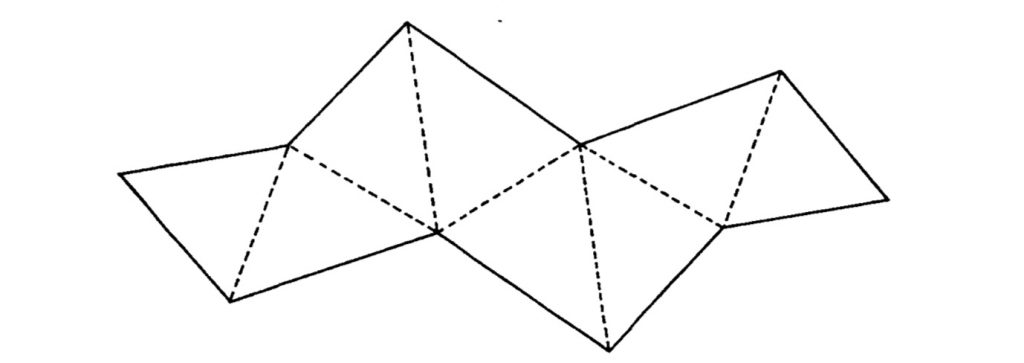
Con el desarrollo de Shephard se pueden construir dos poliedros uno un octaedro y otro de otro tipo combinatorio distinto, los dos convexos. Yo he tenido que imprimir en grande el desarrollo, recortar y doblar para ver cómo este desarrollo lo es de dos poliedros distintos.

¿Qué sabemos sobre el problema de Durero?

(a) Hay ciertos tipos simples de poliedros para los que sabemos que la conjetura es cierta.

(b) Existen poliedros no convexos, no demasiado complicados que no admiten un desarrrollo (ver [8]).

Las aristas que deben cortarse para obtener el desarrollo forman un grafo sobre el poliedro. Este grafo no puede tener ciclos, ya que exigimos que el desarrollo sea conexo. Por tanto el grafo es un árbol. Este grafo ha de conectar todos los vértices del poliedro, en otro caso el desarrollo no sería plano.

La determinación de un desarrollo para un poliedro dado equivale a determinar un grafo con estas dos condiciones: es un árbol que conecta todos los vértices.  En lo que sigue lo llamaremos simplemente árboles.

(c) Catherine Schevon una estudiante de O’Rourke. Consiguió generar poliedros convexos tridimensionales aleatoriamente y en ellos escoger, también aleatoriamente, un árbol que visite todos los vértices, para comprobar si obtenía un desarrollo del poliedro o por el contrario se producían solapamientos. Sus experimentos dieron como resultado que para un poliedro fijo, la proporción de grafos que producían solapamientos se incrementa al aumentar el número de vértices del sólido. Catherine conjetura que al incrementarse el número de vértices esta probabilidad tiende a 1. Es decir, es cada vez mas difícil encontrar desarrollos de los poliedros aleatorios cuando el número de vértices crece. Mas del 90% de los árboles de poliedros con mas de 70 vértices producen solapamiento.

(d) Wolfram Schlickenrieder, alumno de doctorado de Günther Ziegler escogió otro camino.
Definió diversos tipos de árboles que visiten todos los vértices y que parecieran razonables. Por ejemplo, tomando caminos de mínima longitud entre las aristas del poliedro. Pero encontró contraejemplos para cualquier elección razonable de árbol, es decir poliedros en los que los árboles escogidos daban lugar a solapamientos.  Cualquier criterio razonable de elección de árboles conduce en algunos casos a solapamientos.

(e) En 2014 Mohammad Ghomi [7] ha probado que cualquier poliedro puede ser deformado por una transformación afín en otro que sí admite un desarrollo. Esto es notable pues el transformado afín tiene la misma estructura: número de vértices y caras, número de lados de cada cara y la disposición de las mismas. La idea de la prueba es tomar una dirección general y estirar el poliedro en esa dirección, mas o menos hasta que tenga la apariencia de una aguja y finalmente escoger el árbol con ramas con aproximadamente esa dirección.

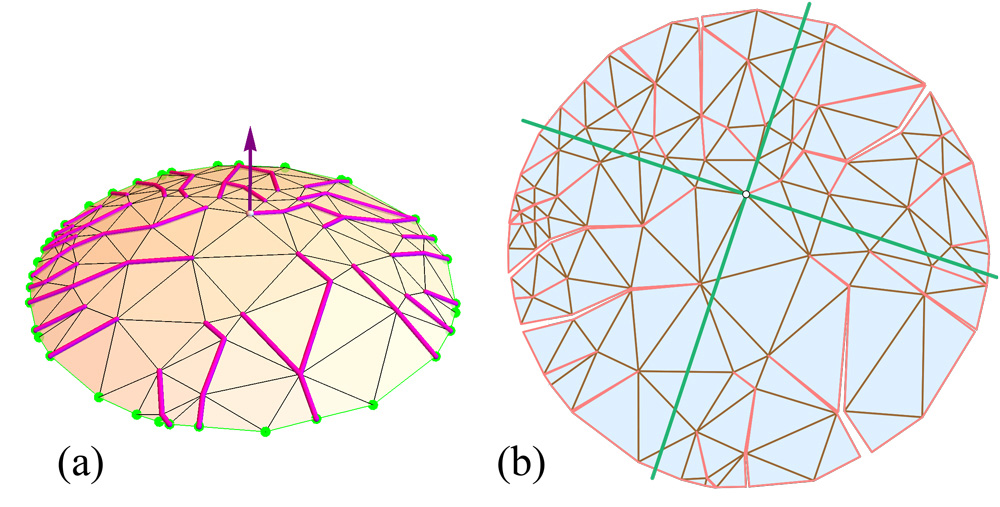
(f) En 2017 O’Rourke [3] ha dado un primer paso en la dirección de probar que todo poliedro con caras triangulares admite un desarrollo. Para ello considera poliedros con una base amplia en el plano xy a la que se superpone una cúpula formada por triángulos, con ángulos agudos. La conjetura es cierta para ciertos tipos de cúpulas con caras triangulares. La figura da un ejemplo de este tipo de cúpulas.

(g) Hay un resultado más, quizás el más importante. Tenemos que aclarar algunos conceptos para poder explicarlo, pero el planteamiento es realmente interesante y da pie para explicar un hermoso teorema topológico de Alexandrov. Así que añadimos este final como un apéndice al que quiera un poco mas.

El teorema de unicidad Alexandrov sobre poliedros

Pensemos en un poliedro convexo como su superficie. Lo consideramos un espacio métrico usando siempre distancias sobre la superficie. Es un espacio geodésico, esto es, la distancia entre dos puntos se realiza siempre mediante una geodésica que los une. Como en la novela Flatland de Abbott pensemos que la superficie del poliedro es un mundo habitado por personajes planos que pueden medir y observar pequeños trozos de su espacio. Nosotros vemos tres tipos de puntos, pero pensemos como lo ven los habitantes de ese mundo:

• Un punto interior de una cara. La geometría en el entorno de este punto es equivalente a la de un punto del plano. Un entorno suficientemente pequeño de este punto es isométrico a un entorno de un punto en el plano euclídeo.
• Un punto del interior de una arista. Los puntos cercanos están en una de las dos caras, pero si giramos las dos caras para que reposen en el mismo plano, vemos que no se alteran las distancias. Desde el punto de vista métrico no observamos diferencia con los puntos de las caras. Si sólo disponemos de las medidas que un habitante de la superficie puede hacer no vemos la diferencia. Los habitantes del poliedro no distinguirán las aristas.
• Un vértice. Si aplanamos las caras que terminan en el vértice vemos que la métrica cercana al vértice no va a ser equivalente a la euclídea. Si un habitante trazara una circunferencia con centro en el vértice y radio pequeño, vería que la circunferencia no es \(=2\pi r\) sino algo menor. Cuánto menor dependerá del vértice y del poliedro. Para cada vértice la longitud de la circunferencia será \(\alpha r\) con \(\alpha<2\pi\). Diremos que \(2\pi-\alpha\) es el defecto del vértice. El habitante de ese mundo distinguiría fácilmente los vértices.

El resumen es que aunque nosotros vemos tres tipos de puntos en un poliedro, desde el punto de vista de un habitante de ese mundo plano solo vería dos tipos: los puntos euclídeos y los vértices. No imaginamos cómo podría distinguir las aristas.

Hay un teorema general para poliedros convexos. La suma de todos los defectos de los vértices es siempre igual a \(4\pi\). Por ejemplo en un cubo todos los vértices tienen el mismo defecto. Pensando un poco vemos que en el caso del cubo el defecto de cada vértice es \(\pi/2\). Como son 8 vértices la suma de defectos es \(8\cdot\frac{\pi}{2}=4\pi\).

Así pues el espacio métrico asociado a la superficie de un poliedro convexo es un espacio métrico tal que salvo por un número finito de puntos, localmente el espacio es euclidiano. En cada vértice la métrica es como la del vértice de un cono con un defecto. Solo hay un número finito de vértices y la suma de sus defectos es \(4\pi\).

Con estos preparativos podemos enunciar el teorema de Alexandrov.

Teorema de unicidad de Alexandrov. Sea \((X,d)\) es un espacio métrico geodésico, homeomorfo a una esfera, y que es localmente euclidiano salvo por un número finito de puntos que localmente son isométricos a vértices de un cono y con defecto total igual a \(4\pi\). Existe entonces un poliedro convexo \(P\) tal que \((X,d)\) es isométrico a la superficie de \(P\) con la distancia geodésica. Además el poliedro \(P\) es único.

Un habitante de un mundo así distinguiría fácilmente los vértices en su mundo. Pero con mediciones locales es difícil que detectara las aristas. Sin embargo por el teorema de Alexandrov las aristas son reales, pero el teorema no es constructivo y no nos dice como definirlas intrínsecamente.

Veamos qué propiedades tienen las aristas: Una arista es siempre una geodésica que une dos vértices. El conjunto de las aristas separa regiones en el espacio que son isométricos a polígonos convexos del plano euclídeo. A cada vértice llegan al menos tres aristas. Pero lo sorprendente es que estas condiciones no solo las verifican las aristas. Por ejemplo, podemos ver en la figura el desarrollo de un cubo y otra descomposición en supuestas aristas que cumplen todas las condiciones que hemos enumerado. El teorema de Alexandrov nos dice que el cubo es el único poliedro que corresponde a este espacio métrico.

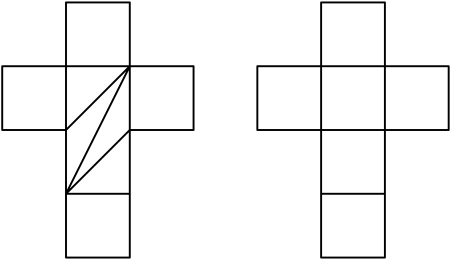
Un día un habitante de uno de estos mundos cúbicos sorprendió a sus congéneres con la teoría de que su mundo se obtenía uniendo cuatro cuadrados y cuatro triángulos de un modo especial. Al cabo de cierto tiempo otro científico mantenía que se obtenía sí, pegando trozos, pero que se trataba de seis cuadrados. Ellos no se ponían de acuerdo.

Sabemos, por el teorema de Alexandrov que el segundo tenía a su lado que en un mundo tridimensional se podía realizar el modelo físicamente. Pero las dos teorías explicaban todos los hechos.

Diremos que las de la izquierda son seudo-aristas. Tenemos ahora las herramientas para explicar el último gran avance en el problema de Durero. Y simultáneamente entender la dificultad del mismo.

Barvinok y Ghomi [9] han construido (siguiendo el camino de una construcción anterior de Alexey Tarasov que no era correcta) un cuerpo convexo y un conjunto de seudo-aristas cumpliendo las condiciones que hemos dicho de manera que con respecto a estas seudo-aristas no existe ningún desarrollo sin solapamiento.

La construcción simplifica mucho la de Tarasov, que necesitaba un poliedro con 19000 vértices. Ellos solo necesitan 176. Como muestra de su construcción incluimos aquí su figura principal.

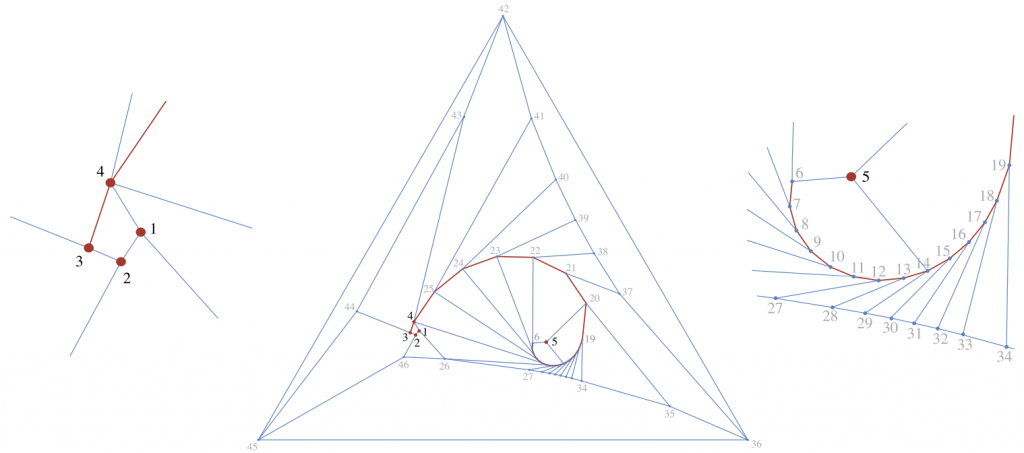
Notemos que esto es casi un contraejemplo al problema de Durero. Cualquier demostración positiva del problema de Durero necesitará distinguir de alguna forma entre aristas y seudo-aristas. Claro que mi fé en que todo poliedro vaya a tener un desarrollo se ha debilitado mucho con esta construcción. Pero es la diferencia entre aristas y seudoaristas la que no entendemos bien y la que puede estar en la base de que el problema tenga una solución positiva.

Para saber mas

La edición traducida del libro de Durero, es difícil de conseguir,  he llegado a verla en internet. Esta edición es posterior y mas completa que la que he podido enlazar arriba.

[1] Dürer, A., De Symmetria Partium in Rectis Formis Humanorum Corporum, Nuremberg, 1532, and Underweysung der Messung, Nuremberg, 1538, Octavo; Multilingual edition (March 2003), CD-ROM 566 pages.

Otro libro interesante es el de Joseph  O’Rourke (professor of Computer Science and of Mathematics at Smith College in Massachusetts in the USA).

[2]   J. O’Rourke, How to Fold It: The Mathematics of Linkages, Origami, and Polyhedra, Cambridge University Press, 2011.

Es un trabajo de O’Rourke, donde prueba su teorema para cúpulas,  el que me ha llevado a escribir esta entrada:

[3]  J. O’Rourke, Edge-Unfolding Nearly Flat Convex Caps, arXiv:1707.01006.

Hay varias exposiciones del tema. Una muy buena es de Mohammad Ghomi

[4] M. Ghomi, Dürer’s Unfolding Problem for Convex Polyhedra, Notices Amer. Math. Soc. 2018.

También es interesante

[5] Malkevitch, J. Nets: A Tool for Representing Polyhedra in Two Dimensions.

Los artículo originales. Los de Ghomi, tienen una introducción bien escrita explicando los problemas.

[6] Shephard, G. C.,  Convex Polytopes with Convex Nets, Math. Proc. Camb. Phil. Soc. 78, 389-403, 1975.

[7] Ghomi, Mohammad, Affine unfoldings of convex polyhedra, Geometry & Topology, 18 (2014) 3055–3090

[8] Bern, M.; Demaine, E. D.; Eppstein, D.; and Kuo, E., Ununfoldable Polyhedra. Proc. 11th Canadian Conference on Computational Geometry, pp. 13-16, 1999. Preprint dated 3 Aug 1999. arXiv:cs/9908003

[9] Barvinok, N, Ghomi, M., Pseudo-edge unfoldings of convex polyhedra. 2017. arXiv:1709.04944.