Solución: Tangentes

Publicamos la solución al Divertimento Tangentes. Antonio Velasco, Alberto Castaño y Cristóbal Sánchez-Rubio han propuesto soluciones al problema.

Divertimento:

Consideremos dos números naturales distintos \(n\) y \(m\). Demostrar que, si existe un triángulo con ángulos \(A\), \(B\) y \(C\) tal que $$\tan A = n \qquad \tan B = n + m \qquad \tan C = n − m,$$
entonces ni \(n\) ni \(m\) son divisibles por 3.

Solución:

Solución propuesta por Cristóbal Sánchez-Rubio.

Es sabido que en cualquier triángulo se cumple:

$$ \tan A + \tan B + \tan C =  \tan A \cdot \tan B \cdot \tan C$$

En nuestro caso la igualdad anterior queda

$$3n=n(n+m)(n-m), \qquad n+m=\frac{3}{n-m}.$$

Al ser una ecuación en números naturales, \(n-m\) sólo puede ser 1 o 3 y la única solución válida es \(n=2, m=1\) y los ángulos cumplen

$$\tan A =2, \tan B=3, \tan C = 1.$$

La construcción del triángulo es inmediata sobre una cuadrícula 6 x 6 como se observa en la figura. La comprobación es “sin palabras” y el triángulo obviamente existe.

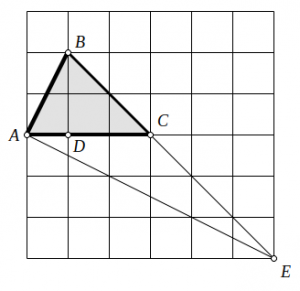
Sus lados son proporcionales a \(\sqrt{5}, 2 \sqrt{2}\) y \(3\).

Se puede generalizar el planteamiento estudiando la existencia de triángulos cuyas tangentes de sus ángulos estén en progresión aritmética. Pongamos por comodidad de escritura \(a=\tan A, b=\tan B, c=\tan C\). Supongamos que el término central de la progresión es \(a\), el menor \(c\) y el mayor \(b\). De una parte si fuese \(A>90^o\), entonces \(B \geq A > 90^o\) lo que es imposible, luego \(A \leq 90^o\), y \(a \geq 0\). Y de otra tenemos las condiciones

$$2a=b+c, \qquad a \cdot b \cdot c = a+b+c,$$

de donde \(b \cdot c =3\). Entonces \(b\) y \(c\) son las raíces de la ecuación \(x^2-2ax+3=0\), es decir,$$b= a + \sqrt{a^2-3}, \qquad c= a – \sqrt{a^2-3}.$$ Esto impone la condición \(a \leq \sqrt{3}\), de donde \(A \geq 60^o\). Resumiendo: para cualquier ángulo \(A\) con \(60^o \leq A \leq 90^o\), existe un triángulo de lados \(A,B,C\) con $$2 \tan A = \tan B + \tan C.$$