Breve historia de Tim Gullikson
Tim Gullikson fue un jugador y entrenador de tenis estadounidense de los setenta a los noventa. Como jugador ganó 15 títulos de la ATP, diez de ellos en dobles junto a su hermano gemelo Tom.

Tras retirarse del circuito profesional, siguió ligado al tenis como entrenador, al servicio de grandes tenistas, entre otros Martina Navratilova. Pero su mayor éxito en esta faceta le vino cuando dirigió los pasos de Pete Sampras, a quien hizo ganar cuatro títulos del Grand Slam y subir en un año del número 21 al número 1 en el ranking mundial.
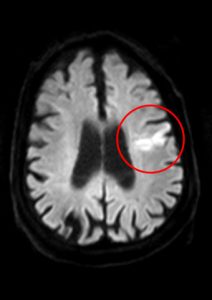
Tristemente, Gullikson es también recordado por un mal diagnóstico médico. En la segunda mitad de 1994, acompañando a Sampras en Europa, sufrió varios desvanecimientos que los neurólogos consultados achacaron a un coágulo de sangre en el cerebro, atribuyéndole origen congénito. Gullikson continuó junto a su pupilo hasta el abierto australiano, en enero de 1995 en Melbourne, donde volvió a quedar inconsciente en una sesión de entrenamientos. De regreso a Estados Unidos, varias semanas después, le fue detectado un tumor cerebral sin operación posible. Murió en mayo de 1996.
Tras su muerte, su hermano gemelo creó la Fundación Tim & Tom Gullikson, cuyo fin es prestar ayuda a pacientes de tumor cerebral y a sus familias.
La Elastografía y las imágenes por resonancia magnética
Posiblemente, Gullikson habría vivido más tiempo si se hubiera sometido a un estudio elastográfico tras su primer desmayo (y tal vez habría conseguido que Sampras jugara bien en tierra batida, algo que nunca sucedió).
La Elastografía es una técnica diseñada para detectar las propiedades elásticas de los tejidos. Permite distinguir en un órgano tejidos sanos (elásticos) de aquéllos que presentan alguna anomalía (generalmente mucho más rígidos). Por este motivo, se recurre a ella con frecuencia cuando se sospecha de la presencia de tumores.
Las principales «herramientas» que intervienen en un estudio elastográfico son:
- Un generador de ondas acústicas (resonancia magnética o ultrasonido).
- Un captor de esfuerzos elásticos.
- Un solver matemático (capaz de analizar, resolver e interpretar la situación).
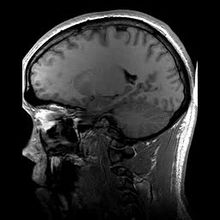
El proceso proporciona una imagen, llamada elastograma, fácil de interpretar, que visualiza la «dureza» de las distintas zonas de la región seleccionada.
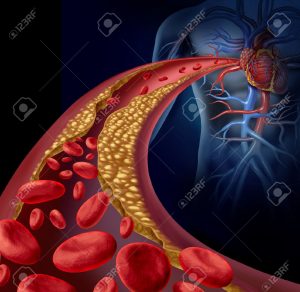
El uso de esta técnica se asocia sobre todo a la detección de tumores. Pero también resulta muy útil para otros fines. Por ejemplo, la Elastografía permite diagnosticar arterioesclerosis, que puede ser definida como el ensanchamiento, endurecimiento y pérdida de elasticidad de las paredes arteriales. También es capaz de detectar fibrosis, esto es, el endurecimiento y posible cicatrización del tejido conectivo, con frecuencia debidos a una lesión.
El problema matemático que hay detrás
En la práctica, todo se reduce a resolver un problema inverso: queremos calcular la solución de un complicado sistema de ecuaciones donde sólo algunos de los datos son conocidos (se desconocen las propiedades elásticas del medio) pero se dispone de una información adicional (la respuesta elástica del medio a las ondas aplicadas).
El sistema toma la forma

$$
E(u,\alpha) = \Phi, \qquad \qquad (1)
$$
donde las funciones \(u\), \(\alpha\) y \(\Phi\) se interpretan, respectivamente, como un campo de desplazamientos determinado por las vibraciones, una matriz de coeficientes asociados a las propiedades elásticas y una onda acústica impuesta. Por otra parte, disponemos de una información adicional \(\Psi\), proporcionada por una observación realizada sobre (parte de) la frontera del órgano.
Si conociéramos \(\alpha\), la teoría matemática sería aplicable y, para cada dato \(\Phi\), podríamos resolver el sistema (1), asegurar la existencia y unicidad de solución y calcular aproximaciones numéricas satisfactorias de \(u\).
Pero \(\alpha\) es desconocido; por tanto, el objetivo está en calcular \(\alpha\) a partir de \(\Phi\) y de la información adicional \(\Psi\).
Más precisamente, conservando el paralelo de nuestra tarea con la que debe
realizar el dispositivo para un estudio elastográfico, se pretende lo siguiente:
- Que el generador de ondas fije los valores de \(\Phi\).
- Que el captor evalúe \(\Psi\).
- Finalmente, que el solver calcule \(\alpha\).
Un método eficiente de resolución
De entre todos los métodos de resolución, el más natural consiste en reformular la cuestión como un problema de mínimos.
La idea es muy simple: para cada eleción de \(\alpha\), denotamos \(u(\alpha)\) la solución de (1) y \(F(\alpha)\) la observación correspondiente a este campo \(u(\alpha)\).

Entonces tratamos de calcular \(\alpha\) en una familia de coeficientes admisibles \(A\) tal que \(F(\alpha)\) sea lo más parecido posible a \(\Psi\):
Min. \({\rm dist} (F(\alpha),\Psi)\), Sujeto a \(\alpha \in A\), \(\ \ \) (2)
donde \({\rm dist} (F(\alpha),\Psi)\) se interpreta como una distancia de la función \(F(\alpha)\) a \(\Psi\).
En la Figura A representamos un tumor \(D\) en un órgano esférico \(\Omega\). Los valores de \(\alpha\) son completamente distintos dentro y fuera de \(D\); aquí, sólo representamos una de las componentes de \(\alpha\), denotada \(\mu\) y denominada coeficiente de Lamé.
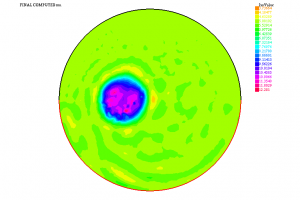
Usando la información \(\Psi\) que proporciona la solución de (1) correspondiente a estos valores de \(\alpha\) y recurriendo a un algoritmo adecuado (de tipo quasi-Newton), hemos sido capaces de resolver el problema (2). El coeficiente \(\mu\) calculado está representado en la Figura B. Vemos pues que es posible detectar la presencia del tumor en estas condiciones. Otras experiencias similares (con uno o varios tumores, con una geometría más compleja, etc.) también conducen a resultados satisfactorios.
Para saber más
Las imágenes e ideas generales han sido tomadas de:
[1] https://en.wikipedia.org/wiki/Elastography
[2] https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5399595/
[3] https://www.healthism.co/arteriosclerosis/
[4] https://www.gchir.mri.tum.de/en/halsschlagader-carotis/
[5] https://www.mayoclinic.org/es-es/diseases-conditions/pulmonary-fibrosis/symptoms-causes/syc-20353690
[6] https://www.netterimages.com/search.htm?keyword=Fibrosis
Para una descripción interesante y completa de los principios y técnicas básicas en Elastografía, ver:
[7] J.-L. Gennison, T. Deffieux, M. Fink, M. Tanter, Ultrasound Elastography: principles and techniques, Diagnostic and Interventional Imaging, Volume 94, Issue 5, May 2013, Pages 487-495.
Finalmente, para los argumentos y resultados matemáticos, teóricos y numéricos, véanse los dos trabajos siguientes y las referencias ahí citadas:
[8] E. Fernández-Cara, F. Maestre, On some inverse problems arising in elastography, Inverse Problems 28 (2012), no.8, Article ID 085001.
[9] E. Fernández-Cara, F. Maestre, An inverse problem in elastography involving Lamé systems, J. Inverse Ill-Posed Probl. 2018; aop, https://doi.org/10.1515/jiip-2017-0065.

Dejar una contestacion