En una entrada anterior hablamos del Programa de Newton, es decir de usar las matemáticas y el método científico para explicar el mundo que nos rodea. Allí vimos que para finales del siglo XIX ese programa estaba, en opinión de la mayoría de los físicos, prácticamente acabado a excepción de las dos nubecillas que mencionó William Thomson (Lord Kelvin) en su conferencia en la Royal Institution el 27 de abril de 1900 titulada Nineteenth century clouds over the dynamical theory of heat and light y cuyo texto luego fue ampliado y publicado en el Philosophical Magazine and Journal of Science en 1901. Concretamente Thomson escribe en su artículo de 1901:
“La belleza y claridad de la teoría dinámica, que establece que el calor y la luz son modos de movimiento, están actualmente oscurecidas por dos nubes. La primera nació con la teoría ondulatoria de la luz y fue abordada por Fresnel y el doctor Thomas Young; involucra la cuestión: ¿cómo podría la Tierra moverse a través de un sólido elástico tal y como esencialmente es el éter? La segunda es la doctrina de Maxwell-Boltzmann relativa a la partición de la energía”.
Como mencionamos en dicha entrada dichas nubes cambiaron por completo la concepción del mundo que nos rodea. La primera condujo a la Teoría de la Relatividad Especial (y luego a la General) de Einstein, y la segunda a la Mecánica Cuántica. En esta entrada vamos a intentar explicar en que consistía esta segunda nubecilla de Lord Kelvin.
Comenzaremos con la afirmación de que “la belleza y claridad de la teoría dinámica, que establece que el calor es un modo de movimiento”. Aquí Lord Kelvin se refiere al hecho de que las leyes de la termodinámica se podían explicar a partir de una teoría mecanicista: La mecánica estadística. La termodinámica es la ciencia que estudia la interacción del calor con el resto de las energías y fue desarrollada casi en su totalidad en el siglo XIX. El auge de la termodinámica seguramente estuvo impulsado por la Revolución industrial y la necesidad de optimizar las máquinas de vapor, motor fundamental de dicha Revolución. Las leyes de la termodinámica eran esencialmente empíricas, basadas en las observaciones, así que en la segunda mitad del siglo XIX se intentó darle una base físico-matemática más rigurosa. ¿Cuál fue la idea? Usar la mecánica de Newton para explicar el comportamiento de las partículas que conforman los sistemas macroscópicos y de esta forma responder a preguntas del tipo ¿cómo se comporta un gas en una habitación cerrada? Dado que una habitación de 36 metros cúbicos hay unas \(10^{27}\) moléculas es imposible usar las leyes de Newton para estudiar el movimiento de las mismas (demasiadas ecuaciones), lo que si se puede hacer es un estudio probabilístico que permita conocer como se comportará en promedio (o en media) el sistema conformado por esa gran cantidad de partículas. Eso es exactamente lo que hace la mecánica estadística tratar estadísticamente el movimiento de un gran número de partículas cada una de las cuales se mueve según las leyes de la mecánica clásica o newtoniana. En otras palabras, la mecánica estadística es la base matemática de la termodinámica. Entre los principales científicos que contribuyeron a crear la mecánica estadística estaban precisamente Ludwig Boltzmann y James C. Maxwell. Pero volvamos a la segunda nubecilla.


La doctrina de Maxwell-Boltzmann que menciona Lord Kelvin no es más que el Teorema de la equipartición de la energía que establece que la energía calorífica de un conjunto de partículas se divide uniformemente entre todas las posibles componentes de los movimientos de cada una de las partículas, o como suelen decir los físicos, en cada uno de los grados de libertad del sistema. Por ejemplo, si consideramos que las partículas son pequeñas bolas que se mueven en una habitación, la energía calorífica (que es el resultado del movimiento de las bolas y los choques entre las mismas) se dividirá por igual en las tres componentes x, y y z (coordenadas cartesianas) en las que se descompone en movimiento. Este Teorema fue enunciado por Ludwig Boltzmann en 1868 (quién generalizó un principio propuesto por John J.Waterston en 1845) y demostrado en condiciones mucho más generales por James C. Maxwell en 1879. Desde la publicación del trabajo de Boltzmann, y en especial del de Maxwell hubo mucha controversia sobre la veracidad del mismo. Entre los que hicieron aportes relevantes se encontraban el propio Lord Kelvin, James Jeans y Lord Rayleigh. Este último escribió en en año 1900 un interesante artículo sobre el tema donde ponía de manifiesto las contradicciones a las que se podía llegar al usar el Teorema de Maxwell-Boltzmann.
Ahora retrocedamos unos años y abordemos otro problema de gran interés a mediados del siglo XIX: el problema de como absorbían y emitían radiación los cuerpos calientes. La historia de este fenómeno es muy interesante aunque aquí nos restringiremos a mencionar el hecho de que a finales del siglo XIX había un modelo prácticamente aceptado por todos los físicos para describir el fenómeno: el modelo del cuerpo negro introducido por el físico alemán Gustav Kirchhoff en 1860. Todos sabemos que al calentar un cuerpo este cambia de color (quién no ha calentado de pequeño un clavo o un tornillo en el fogón de casa o ha visto el color que toma una parrilla al hacer una parrillada). Así que ya tenemos una pregunta interesante: ¿cómo emiten luz los cuerpos al calentarse? Para resolver este problema precisamente los físicos de finales del siglo XIX desarrollaron el modelo del cuerpo negro. Un cuerpo negro era un cuerpo ideal que absorbía y emitía ondas electromagnéticas en todo el espectro de frecuencias pues era un hecho bien conocido a finales del XIX que la luz visible estaba constituida por ondas electromagnéticas dentro de un cierto rango de frecuencias. Como se comprobó más adelante, también absorbía y emitía fuera de ese rango, en lo que se llamó región ultravioleta (frecuencias muy altas) e infrarojas (frecuencias muy bajas) del espectro electromagnético.
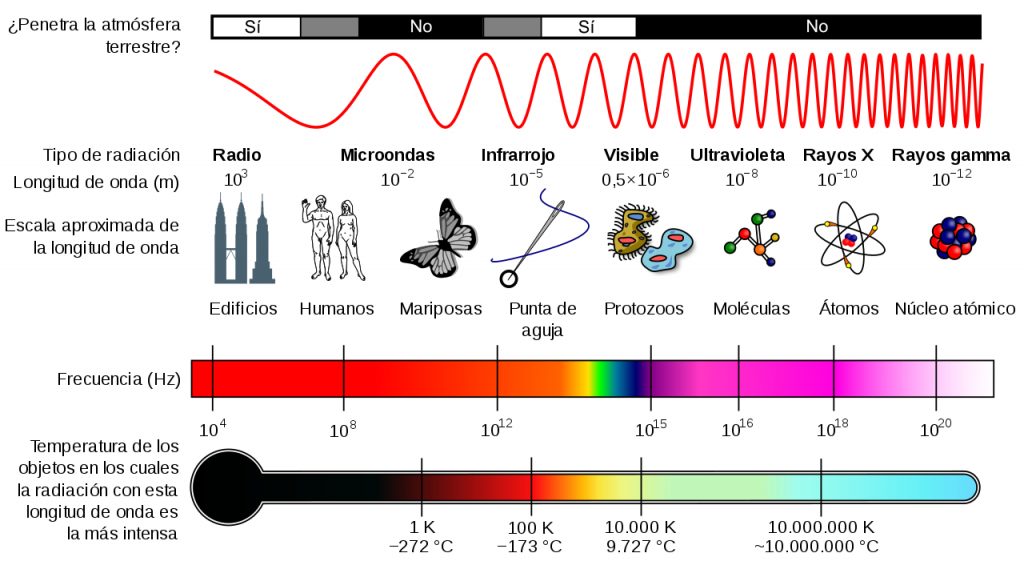
Imaginemos ahora que tenemos un cuerpo negro a una temperatura T. Denotemos la densidad de energía (es decir, la cantidad de energía por unidad de volumen) por \(U(T)\) (ya que obviamente dicha densidad de energía dependerá de la temperatura T a la que se encuentra el cuerpo). Dado que el cuerpo emitirá radiación electromagnética en todas las frecuencias de onda posibles asumiremos que cada frecuencia aportará su «granito de arena» al total. Así, si conocemos el valor de energía \(u(\omega,T)\) que aporta cada frecuencia \(\omega\) y los sumamos todos obtendremos la energía total que emite nuestro cuerpo negro. Metidos de lleno en el problema los físicos se lanzaron a estudiar como emitían luz los cuerpos. Este problema era además de gran interés industrial pues justo a finales del siglo XIX empezaron a utilizarse las bombillas eléctricas para el alumbrado público y el problema de la conversión de energía calorífica en luminosa era de gran importancia.
El primero en establecer una ley empírica para la radiación del cuerpo negro fue el físico alemán Friedrich Paschen quien en 1896 publicó, basándose en observaciones experimentales, que
\(u(\omega,T)=\alpha \omega^3 e^{-\beta \omega/T}.\)
Ese mismo año, un poco antes de que apareciera el artículo de Paschen, otro físico alemán Wilhelm Wien, obtuvo la misma fórmula pero basándose en razonamientos teóricos. En ambos casos los valores de \(\alpha\) y \(\beta\) debían obtenerse a partir de los datos experimentales. Conviene destacar que la fórmula de Paschen-Wein solo explicaba razonablemente bien la parte ultravioleta, es decir las altas frecuencias del espectro de emisión de un cuerpo negro y fallaba en la banda infrarroja o de bajas frecuencias, aunque en su defensa hay que decir que en ese rango de frecuencias había todavía muy poca evidencia experimental. Es aquí donde entra por primera vez en nuestra historia Max Planck quién estaría destinado a hacer desaparecer la segunda nube de Thomson y provocar una de las mayores revoluciones de la Ciencia. Plank no estaba convencido en la forma que Wein había «deducido» la función \(u(\omega,T)\) así que una serie de trabajos partiendo de los principios más generales posibles de la electrodinámica y la termodinámica deduce la fórmula de Wein y calcula los valores de las constantes \(\alpha\) y \(\beta\) a partir de los datos experimentales.
Aunque en apariencia la teoría y los experimentos parecían coincidir existía una corriente de opinión (liderada por el propio Wein) que argumentaba que la suposición de que el cuerpo negro absorbía la radiación de la misma forma independientemente de la frecuencia no era correcta. No mucho después se comprobó que para temperaturas altas y frecuencias bajas (longitudes de onda grandes) \(u(\omega,T)\sim T\) tal y como dedujo Lord Rayleigh en un artículo aparecido en junio de 1900. De hecho Rayleigh demostraba que \(u(\omega,T)\) debía tener la forma
\(u(\omega,T)= a {\omega^2} T, \)
que obviamente no es compatible con la ley de Wein antes mencionada. La fórmula de Rayleigh tenía un problema añadido: si cada frecuencia aportaba una energía como la que Rayleigh proponía, entonces la suma de todas ellas (que habría que calcularla mediante una integral \(U(T)=\int_0^\infty u(\omega,T)d\omega\)) tendría que ser infinita lo cual no tenía ningún sentido. Esta fue la llamada catástrofe ultravioleta. Y ¿cuál es la conexión de lo anterior con la segunda nubecilla de Lord Kelvin? Pues que en la derivación de las fórmulas de Wein y Rayleigh se usaba el principio de la equipartición de la energía, y se asumía que el cuerpo negro absorbía (y emitía) la energía de forma continua en todo el rango de frecuencias posibles.
¿Cómo se resolvió este problema? Pues en apariencia de forma muy sencilla. Plank, el mismo que había dado una elegante demostración de la fórmula de Wein, se aventuró a formular una hipótesis arriesgada: ¿y si la energía solo se puede absorber o emitir en cantidades finitas o quanta (como él les llamó)? Los resultados de semejante hipótesis iban a cambiar la concepción del mundo de una manera que nadie preveía, pero eso lo contaremos en una próxima entrada.
Lectura recomendada: Capítulo 1 de J. Mehra y H. Rechenberg, The Historical Development of Quantum Theory, Vol 1. The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900-1925, 1982 Springer-Verlag New York Inc.

Dejar una contestacion