Paralogismo

Delantal:

La lengua española cuenta con un divertido catálogo de frases hechas dotadas de un significado bien distinto del literal, como estar hasta las narices, tomar el pelo, dar la cara o ser un chorizo (casualmente, los ejemplos escogidos se dirigen a menudo a la clase política, pero esa es otra historia). El Divertimento de hoy está relacionado con el significado literal de la expresión borrón y cuenta nueva, o más bien, con su negación: encontrar el error en un razonamiento dado.

Divertimento:

En un viejo tratado de Metodología, dos conocidos profesores españoles dedican un capítulo a tratar los paralogismos o falsas demostraciones que conducen a conclusiones absurdas. Presentamos en este divertimento una de ellas invitando a los lectores a no dejarse engañar.

Teorema. Cualquier ángulo es recto.

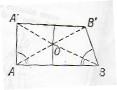
Demostración. Sobre un segmento \(AB\), se levanta el segmento \(AA’\) perpendicular y el oblícuo \(BB’\) de igual longitud. Las mediatrices de los lados \(AB\) y \(A’B’\) se cortan en un punto \(O\) que puede estar en el interior del cuadrilátero \(AA’BB’\). Los triángulos \(OAA’\) y \(OBB’\) son iguales por ser \(OA=OB\) y \(OA’=OB’\) (por pertenecer \(O\) a las mediatrices) y \(AA’=BB’\) por construcción. Por tanto son iguales los ángulos \(A’AO=B’BO\) y \(OAB=OBA\). Sumando estas igualdades resulta que \(\pi/2=A’AB=B’BA\).

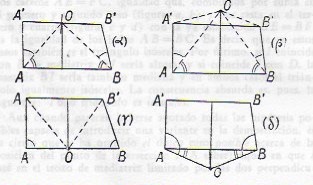
Si el punto \(O\) está sobre el segmento \(A’B’\), sobre el segmento \(AB\), por encima de \(A’B’\) o por debajo de \(AB\), el razonamiento es análogo.

Soluciones:

Envía tus soluciones, antes del domingo 9 de diciembre, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el miércoles 12 de diciembre. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.