En esta entrada vamos a continuar la historia que comenzamos en la entrada anterior: la historia de cierta nubecilla obscura que nublaba el despejado cielo de la física clásica. Como contamos allí, todo empezó con el problema de cómo absorbían y emitían calor los cuerpos calientes. La primera explicación teórica plausible de como era el espectro de radiación de un cuerpo negro (modelo desarrollado para resolver el problema) se debió al físico Wilhelm Wien quién dio una explicación teórica en 1896 a la fórmula encontrada experimentalmente por Friedrich Paschen ese mismo año. La fórmula de Paschen-Wein se escribe como sigue
$$ u(\omega,T)=\alpha \omega^3 e^{-\beta \omega/T},$$
donde \(u(\omega,T)\) es la densidad de energía por unidad de volumen y de frecuencia \(\omega\) emitida por un cuerpo negro, \(T\) es la temperatura y \(\alpha, \beta\) ciertas constantes.

Dicha fórmula reproducía muy bien los resultados experimentales para frecuencias \(\omega\) grandes, pero fallaba estrepitosamente al intentar explicar lo que ocurría para frecuencias pequeñas. En este último caso Lord Rayleigh en 1900 había encontrado que \(u(\omega,T)\) debía ser proporcional a \(\omega^2\) y a \(T\), o sea, \(u(\omega,T)= a {\omega^2} T,\) lo que condujo a la llamada “catástrofe ultravioleta”, ya que al sumar todas las contribuciones de cada una de las frecuencias se obtenía que la densidad de energía de un cuerpo negro debía ser infinita, algo claramente sin sentido. Como ya adelantamos en la entrada anterior, quién finalmente consiguió resolver el problema fue Max Planck, y lo hizo introduciendo un concepto revolucionario: los “quanta” de energía.
Vamos a intentar dar un bosquejo del razonamiento de Planck. Para obtener la fórmula de Wein, Planck asumió que el cuerpo negro estaba constituido por “resonadores”, que eran una especie de osciladores eléctricos cuya frecuencias de oscilación coincidía con las frecuencias de la radiación electromagnética (la forma en que interaccionaba el oscilador con la radiación estaba relacionada con el fenómeno de la resonancia, fenómeno que era conocido desde hacía mucho tiempo). Conviene hacer notar que a finales del siglo XIX todavía no se había establecido la composición de la materia tal y como la conocemos hoy día (átomos formados por un núcleo y con los electrones “girando” a su alrededor) por lo que la suposición de Planck no era del todo descabellada. Lo primero que hizo Planck fue explicar como sus resonadores absorbían y emitían radiación dedicándole varios trabajos al tema entre 1895 y 1896. En esos trabajos Planck también tenía otro objetivo: definir el concepto termodinámico de entropía en la mecánica y el electromagnetismo de forma “racional”. Pero ¿qué es eso de la entropía? Antes de seguir, intentemos explicar qué es la entropía.
La entropía es un concepto que introdujeron los físicos del siglo XIX para poder escribir correctamente y de forma completa las famosas leyes de la Termodinámica (concretamente el físico y matemático alemán Rudolf Clausius fue quien la introdujo en 1850), aunque fue Ludwig Boltzmann (del que ya hablamos en la entrada anterior) quién, al desarrollar la mecánica estadística, le dio la formulación matemática (y la interpretación física) que usamos hoy día y que involucra las probabilidades. Y precisamente esa idea no gustaba a Planck (y no solo) pues un argumento probabilístico implicaba el no determinismo de las leyes físicas. El concepto de entropía es un concepto matemático con muchas sutilezas. Una de las interpretaciones habituales consiste en afirmar que la entropía es una cantidad matemática que mide el grado de desorden (o del orden si se prefiere) de un sistema físico. Esto puede crear algunas confusiones, por ejemplo: ¿dónde hay más orden, en un vaso de agua, o en uno con un montón de trozos de hielo? (muchas personas responden que los trozos de hielo de un vaso están más desordenados que el agua que queda en el vaso después de que derritan dichos hielos). Siendo serios, para responder adecuadamente a esta pregunta tendríamos en primer lugar que definir de alguna forma que es el orden en un sistema físico.
Veamos una forma “relativamente” sencilla de entender el concepto de entropía. Para ello tendremos que recurrir a lo que hoy día se conoce como fórmula de Boltzmann. Según esta fórmula la entropía \(S\) de un sistema de partículas se expresa mediante la fórmula \(S=k \ln \Omega\), donde \(k\) es una constante positiva y \(\Omega\) es en número de “microestados” del sistema. Aclaremos esto con un simple ejemplo. Por simplicidad imaginemos que tenemos un sistema con cuatro partículas confinadas en una caja. Imaginemos ahora que sabemos que las cuatro partículas están a la izquierda de la caja (lo que denominaremos estado A). La única posibilidad de tener ese estado (cuatro partículas a la izquierda) está representada en la siguiente figura
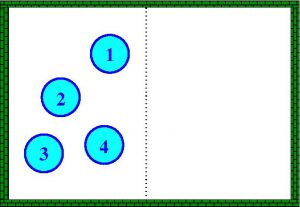
Es decir, el estado A solo puede estar constituido por un único “microestado”. Si ahora sabemos que el estado de nuestro sistema es que hay tres a la izquierda y una a la derecha (estado B), entonces hay cuatro formas posibles (cuatro “microestados”) de que ocurra:
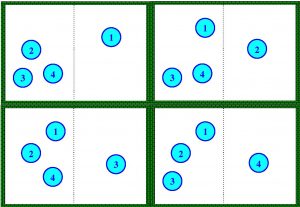
Es natural pensar que en nuestro ejemplo el estado A es más ordenado que el B. Si usamos la fórmula de Bolztmann, entonces el estado A tiene una entropía igual a \(S=k \ln 1 =0\) menor que el B que es igual a \(S=k \ln 4\). Impongamos ahora que para nuestro sistema de cuatro partículas cada “microestado” es igual de probable, es decir, cada microestado ocurre con igual probabilidad. Entonces, está claro que es cuatro veces más probable encontrar al sistema en el estado B que en el A, así, si tenemos cuatro partículas en la caja es mucho más probable que el sistema se encuentre en el estado de mayor entropía (el estado B) que en el de menor entropía (estado A). De hecho, la posibilidad de encontrar nuestro sistema en un estado con dos partículas a la izquierda y dos a la derecha es 6 veces mayor que que todas estén a la izquierda. Si en vez de tener 4 partículas tenemos 100 entonces el estado cuando las cien están a la izquierda solo tiene una posibilidad, mientras que el estado de tener 50 y 50 es posible tenerlo de \(10^{29}\) formas, o sea, es casi seguro que nuestro sistema se encuentre en un estado más cercano al de 50 y 50 que en el de las 100 a la izquierda (imaginad que ocurre en una habitación donde hay \(10^{27}\) partículas). En otras palabras todas los sistemas tienden al estado de máxima entropía por pura probabilidad (hay muchos más estados con las partículas dispersas en ambos lados que con las partículas concentradas en uno de los lados). Si decimos ahora que un estado es más desordenado que otro si hay más formas distintas de obtener dicho estado a partir de sus «microestados», entonces está claro que el estado 2 y 2 (o 50 y 50) es más desordenado que el 4 y 0 (o 100 y 0). Precisamente una de las formas de escribir el segundo principio de la Termodinámica consiste en decir que todo proceso termodinámico tiende al máximo de entropía, o lo que es lo mismo, que todo sistema físico tiende a estar lo más desordenado posible (en el sentido de la definición anterior).
Era toda esta historia probabilística, además del hecho de no tener claro como usarla en el contexto de la electrodinámica, lo que no le gustaba a Plack de la teoría de Boltzmann. Y no solo a Planck. De hecho el rechazo a su teoría cinética (que implicaba la asunción de que los gases estaban formados por pequeñas partículas -teoría atómica- en constante movimiento, algo que no estaba experimentalmente determinado a finales del siglo XIX y lo que regresaremos en otra ocasión) por parte de gran parte de la comunidad científica pudo ser una de las causas del suicidio de Bolztmann en 1906.
Sigamos. Aparte de la cuestión probabilística anterior también había otro espinoso asunto. Para Boltzmann (al igual que para Maxwell, de quién también hablamos en la entrada anterior) los gases estaban constituidos por partículas que chocaban unos con otros siguiendo las leyes de la mecánica clásica de Newton. Pero entonces surgía un grave problema tal y como puso de manifiesto el asistente de Planck en Berlín, Ernest Zermelo (y sí, es el mismo Zermelo de la teoría de conjuntos y la lógica matemática, al cual le debemos el controvertido pero muy útil axioma de elección). El problema consistía en unos años antes, en 1890, Heni Poincairé había probado que cualquier sistema mecánico como el que proponía Boltzmann (constituido por muchas partículas cuyo movimiento obedecía las leyes de la mecánica de Newton) regresaría tarde o temprano (aunque pudiese tardar toda una eternidad) al mismo estado del que partió (o a cualquiera de los estados por donde pudiese haber estado en algún momento). En otras palabras, la mecánica estadística de Boltzmann describía procesos que eran irreversibles según la termodinámica (por ejemplo el proceso de difusión de un gas en una habitación es irreversible, ya que si inicialmente tenemos todo el gas en una esquina de una habitación, este siempre se va dispersar por toda la habitación y nunca se va a concentrar otra vez en la esquina de la misma) pero las propias bases de su teoría descansaban sobre la mecánica newtoniana que era de por si determinista y por tanto sólo podía describir procesos reversibles tal y como había probado Poincaré.
Pero regresemos a nuestra historia. Plank dedicó varios años a estudiar como poder usar el concepto de entropía en el contexto de la radiación electromagnética usando sus resonadores e introduciendo un concepto que llamo “radiación natural” y publicó varios trabajos hasta principios del año 1900. Entre los resultados que publicó en 1900 estaba su aportación al problema del espectro de emisión de un cuerpo negro, asumiendo, como ya mencionamos, que este estaba compuesto por sus resonadores. De hecho, la prueba de Planck de la fórmula Paschen-Wein era bastante simple y más elegante que la del propio Wein y como ya mencionamos se correspondía muy bien con los resultados experimentales de la época. Ahora bien, era bien sabido que la fórmula Wein funcionaba muy bien en la zona del espectro de frecuencias grandes, pero ¿y en el las zonas de bajas frecuencias? En la zona de bajas frecuencias apenas había resultados experimentales hasta la primera mitad del año 1900. Las primeras mediciones precisas de la densidad de energía para el cuerpo negro en la región de las bajas frecuencias las realizaron dos físicos alemanes Heinrich Rubens y Ferdinand Kurlbaum. El 7 de octubre de 1900 y antes de publicar sus experimentos el propio Rubens discutió con Planck durante una visita a su casa sus resultados experimentales para bajas frecuencias que además, según sus propias palabras (de Rubens), encajaban perfectamente con la fórmula deducida por Lord Rayleigh ese mismo año, es decir, que para altas temperaturas y longitudes de onda largas (o sea, bajas frecuencias) \(u(\omega,T)= a {\omega^2} T\). Inmediatamente Planck se puso a modificar su prueba de la fórmula de Wein para intentar dar cabida a los nuevos resultados experimentales que le acababa de contar Rubens. Esa misma tarde (del 7 de octubre de 1900) Plack envió a Rubens su deducción de una nueva fórmula para la densidad de energía \(u(\omega,T)\) y Rubens le confirmó que la nueva fórmula encajaba perfectamente con sus resultados experimentales. La fórmula que Planck derivó era la siguiente
$$ u(\omega,T)=\frac{a \omega^3}{ \exp\left({\frac{ b \omega}{kT}}\right)-1 }$$
que tiene una propiedad sumamente interesante: si \(\omega\) es pequeña entonces \(u(\omega,T)\sim \omega^2 T\) lo que concordaba con la fórmula de Rayleigh y si \(\omega\) era muy grande, se recuperaba la formula de Wien.
El 9 de octubre de 1900 Kurlbaum presentó los resultados experimentales en la reunión de la Sociedad alemana de Física y durante la discusión de los mismos Planck anunció que había encontrado una mejora de la fórmula de Wein, una fórmula que concordaba muy bien con los experimentos en todo el rango de longitudes de onda (o frecuencias) del espectro electromagnético. Tras esa sesión todo parecía indicar que se la segunda nubecilla de Lord Kelvin había sido eliminada para siempre de la Física clásica pues se había conseguido encontrar la expresión para la distribución de la energía de la radiación de cuerpo negro pero …
Si querido lector, siempre hay un pero. En su razonamiento, Planck había hecho una suposición sobre la expresión matemática que debía tener de la entropía del cuerpo negro que no estaba respaldada por ninguna teoría física (es, como llamamos ahora, una teoría fenomenológica), así que decidió encontrar una justificación racional (o sea rigurosa), desde los primeros principios, tal y como se establecía en lo que llamamos el Programa de Newton. Planck estaba convencido que todo su trabajo previo sobre resonadores podía ayudarle a resolver este último escollo. Aunque es difícil dar una idea de los razonamientos de Planck sin usar las matemáticas superiores, vamos a intentar al menos dar una idea intuitiva de su razonamiento. Dado que Planck usaba ciertas expresiones para la entropía decidió dejar a un lado al menos momentáneamente su aversión por el uso de las probabilidades y profundizar en el trabajo de Boltzmann.
Lo primero que hizo Planck después de releer el trabajo de Boltzmann fue escribir la fórmula de la entropía \(S=k \ln \Omega\) que vimos antes para un conjunto de elementos, donde \(\Omega\) es el número de permutaciones de los distintos elementos que componen el sistema y que no cambiaban el estado macroscópico del mismo. O sea, Planck recuperó la argumentación probabilística de Boltzmann. ¿Cómo fue capaz Planck de asumir la hipótesis probabilística que con tanto ahínco había rechazado poco tiempo antes? Él mismo lo explicó 30 años más tarde en una carta al físico Robert Williams Wood escrita el 7 de octubre de 1931:
En resumen, lo que hice puede ser descrito simplemente como un acto de desesperación. Por naturaleza soy pacífico y opuesto a aventuras dudosas. Sin embargo, ya había luchado sin éxito durante seis años con el problema del equilibrio entre la radiación y la materia sin llegar a ningún resultado exitoso. Era consciente de que el problema era de fundamental importancia en la física y conocía la fórmula que describía la distribución de energía en el espectro normal [del cuerpo negro]. Por lo tanto, una interpretación teórica tenía que ser encontrada a cualquier costo, sin importar cuán alta pudiera ser.
De hecho, la fórmula a la que se refiere aquí Planck era la que había había encontrado tras la visita de Rubens a su casa. Usando los datos experimentales dicha fórmula se podía escribir como
$$ u(\omega,T)=\frac{8\pi h \omega^3}{c^3}\frac{1}{ \exp\left({\frac{ h\omega}{kT}}\right)-1 },$$
donde \(h=6.55 \cdot 10^{-27} (erg\cdot seg)\), \(c\) es la velocidad de la luz y \(k\) es la constante de Boltzmann.
Armado con la expresión de Boltzmann para la entropía Planck la aplicó a la radiación del cuerpo negro. Para ello supuso que dicho cuerpo estaba constituido por \(N\) resonadores con frecuencia \(\omega\). Entonces, en palabras de Planck
Si E se considera una cantidad infinitamente divisible, entonces la distribución de E en los N resonadores se puede hacer de infinitas maneras. Sin embargo vamos a considerar que E está compuesta por un número finito de partes iguales y usaremos para este propósito la constante natural \(h=6.55 \cdot 10^{-27} (erg\cdot seg)\). Esta constante multiplicada por el valor \(\omega\) de la frecuencia de los resonadores, nos da el número de elementos de energía \(\epsilon\) a distribuir en los N resonadores.
El resto es mucho más técnico, pero ya todo estaba dicho: la energía E no podía dividirse infinitamente, tenía que absorberse y radiarse en porciones finitas determinadas por la frecuencia \(\omega\) de la radiación (que correspondía a la frecuencia propia del correspondiente resonador). Ese era el precio que había que pagar para que no se hundiera el resto de las leyes de la termódinamica (según Planck era eso o renunciar a las irrenunciables leyes de la termodinámica).
Planck expuso sus resultados el 14 de diciembre de 1900 en la reunión de la Sociedad alemana de Física en una ponencia titulada “Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum” (Sobre la teoría de la ley de distribución de energía en el espectro normal) publicada luego en Verh. d. Deutsch. Phys. Ges. (2) 2, 237-245. Ese día, como escribió años después el gran físico teórico alemán Arnold Sommerfeld en su libro Atombau und Spektrallinien (Estructura atómica y líneas espectrales) de 1919, nació la teoría cuántica y con ella una nueva física que cambiaría el mundo. La teoría cuántica de Planck no gustó a todos, no obstante a ello, conviene comentar que en los años siguientes tanto el propio Planck como otros físicos propusieron formas más simples de deducir la fórmula y por otro lado, se realizaron gran cantidad de experimentos que confirmaban la veracidad de la la fórmula de Planck. El “quanto de acción de Planck” (como lo bautizaron luego) había llegado a la Física, y había llegado para quedarse. Lo que parecía un artificio matemático se convirtió en unas de las ideas más perturbadoras de principios del siglo XX como luego puso de manifiesto el protagonista de nuestra próxima historia: Albert Einstein.

Si quieres saber más:
Capítulo 1 de J. Mehra y H. Rechenberg, The Historical Development of Quantum Theory, Vol 1. The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld: Its Foundation and the Rise of Its Difficulties 1900-1925, 1982 Springer-Verlag New York Inc.
Una introducción en 5 minutos de termodinámica la tienes en este video y de la entropía en este otro.

Dejar una contestacion