Publicamos la solución al divertimento Paralogismo. Gracias a Javier Linares Torres, Rubén Alba Bermúdez y Cristóbal Sánchez-Rubio por las soluciones que nos han hecho llegar.
Divertimento:
En un viejo tratado de Metodología, dos conocidos profesores españoles dedican un capítulo a tratar los paralogismos o falsas demostraciones que conducen a conclusiones absurdas. Presentamos en este divertimento una de ellas invitando a los lectores a no dejarse engañar.
Teorema. Cualquier ángulo es recto.
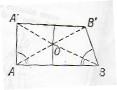
Demostración. Sobre un segmento \(AB\), se levanta el segmento \(AA’\) perpendicular y el oblícuo \(BB’\) de igual longitud. Las mediatrices de los lados \(AB\) y \(A’B’\) se cortan en un punto \(O\) que puede estar en el interior del cuadrilátero \(AA’BB’\). Los triángulos \(OAA’\) y \(OBB’\) son iguales por ser \(OA=OB\) y \(OA’=OB’\) (por pertenecer \(O\) a las mediatrices) y \(AA’=BB’\) por construcción. Por tanto son iguales los ángulos \(A’AO=B’BO\) y \(OAB=OBA\). Sumando estas igualdades resulta que \(\pi/2=A’AB=B’BA\).
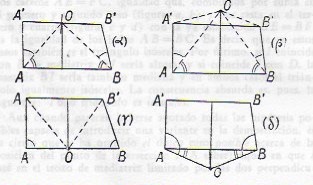
Si el punto \(O\) está sobre el segmento \(A’B’\), sobre el segmento \(AB\), por encima de \(A’B’\) o por debajo de \(AB\), el razonamiento es análogo.
Solución:
Solución propuesta por Cristóbal Sánchez-Rubio.
El razonamiento es falso desde la afirmación \(OAB=OBA\). No son iguales, son opuestos. Suponiendo como es habitual ángulos positivos en el sentido contrario a las agujas del reloj y que el sentido del ángulo es el del giro para llevar el punto \(Y\) sobre la semirrecta \(OX\), resulta que \(OAB\) es positivo pero \(OBA\) es negativo.
La figura de la izquierda muestra la situación cuando \(O\) está en el semiplano superior determinado por \(AB\).
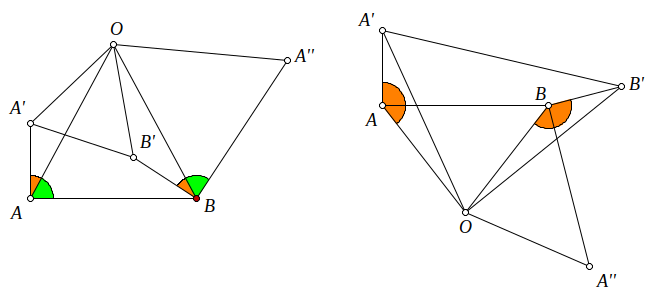
El razonamiento correcto sería construir el simétrico \(A\) respecto de la recta \(OB\) y el ángulo \(OBA^{\prime\prime}\) es el opuesto a \(OBA\) y las igualdades para sumar serían \(A’AO=B’BO\) y \(OAB=OBA^{\prime\prime}\), de donde \(A’AO+OAB=A’AB=\pi/2=B’BO+OBA^{\prime\prime}=B’BA^{\prime\prime}\).
No estamos sino constatando que el triángulo \(A’AB\) rectángulo en \(A\) por construcción se transforma en \(B’BA^{\prime\prime}\) mediante el giro de centro \(O\) y amplitud \(OA’B’\).
La situación es análoga si \(O\) está en el otro semiplano como muestra la figura de la derecha los razonamientos son análogos. Los signos de los ángulos implicados se resumen en el siguiente cuadro:
![]()

Dejar una contestacion