Un problema asequible.
I always kept two problems in mind, one which I want to solve and another which I can solve, decía Jean Bourgain, recientemente fallecido. De vez en cuando viene bien dedicar tiempo a un problema asequible. Y hoy presentamos uno de este tipo. Desde que lo vi planteado este mes de junio en un trabajo en arXiv me gustó y pensé que era un problema asequible. No me equivoqué, acababa de escribir una primera versión de esta entrada el primer fin de semana de febrero cuando el lunes siguiente apareció la nueva versión del trabajo en que resolvían la cuestión.
El problema a que me refiero fue propuesto en junio de 2018 por Javier Soria, catedrático de Análisis Matemático en la Universidad de Barcelona y Pedro Tradacete profesor en el Departamento de Matemáticas de la Universidad Carlos III de Madrid en un trabajo en arXiv.
A pesar de que el problema se ha resuelto ya, voy a plantearlo tal como yo lo vi en junio, después hablaremos de la solución y de un problema de formulación elemental que me sugiere este problema y que creo merecerá vuestra atención.


Trataremos de explicar los conceptos que intervienen en el enunciado antes de exponerlo.
Espacios métricos.
Estamos acostumbrados a hablar de la distancia entre dos puntos. Por ejemplo entre puntos del plano tenemos la distancia usual \(d(a,b)\) entre los puntos \(a\) y \(b\) cualesquiera. Esa distancia cumple varias condiciones simples:
- La distancia es siempre positiva y vale \(0\) solo en el caso de que los dos puntos coincidan.
- La distancia es simétrica \(d(a,b)=d(b,a)\).
- Se verifica la desigualdad triangular, \(d(a,b)\le d(a,c)+d(c,b)\). (para ir de \(a\) a \(b\) es mejor no tener que hacer un recado en \(c\)).
Pero con frecuencia nos encontramos con otros espacios y otras distancias. Por ejemplo cuando viajamos en avión los puntos son los de una esfera y las distancias se miden en arcos de circunferencias. Pero en matemáticas nos encontramos con muchos ejemplos interesantes. Por eso definimos un espacio métrico \((X,d)\) como un conjunto \(X\) dotado de una distancia entre sus puntos que cumpla las condiciones anteriores.
Si tenemos un espacio métrico \((X,d)\) consideraremos las «bolas» del espacio, dado un punto \(a\in X\) y un número real y positivo \(r>0\) la bola \(B(a,r)\) es el conjunto de puntos \(x\) de \(X\) cuya distancia a \(a\) es \(d(a,x)<r\).
Medidas.
También es una idea que nos viene de la geometría. A cada conjunto (razonable) del plano le hacemos corresponder su área. Al conjunto \(A\) su medida \(\mu(A)\). Esta medida cumple unas condiciones. Solo destacaremos algunas que necesitaremos
- La medida es positiva \(\mu(A)\ge0\).
- Si \(A\) es disjunto con \(B\) la medida es aditiva \(\mu(A\cup B)=\mu(A)+\mu(B)\). La medida de la unión es la suma de las medidas.
Entre las dos se sigue que la medida es monótona. Pues si \(A\) es parte de \(B\), es decir, \(A\subset B\) entonces \(B\) es la unión disjunta de dos conjuntos \(A\cup(B\setminus A)=B\) y por tanto \(\mu(A)\le \mu(B)\).
El área tiene muchas otras propiedades interesantes, pero en muchas ocasiones estamos interesados en medidas más generales. Por ejemplo podemos estar interesados en medir la cantidad de agua que hay en cada trozo de espacio. Esa medida será muy diferente si el volumen que medimos esta lleno de aire o es parte del océano. Es una medida diferente a la del volumen.
Una medida \(\mu\) en un espacio \(X\), asignará un número positivo \(\mu(A)\) a ciertas partes de \(X\) de manera que se cumplan las condiciones indicadas anteriormente. Técnicamente hablamos de medidas de Borel, pero para nosotros será suficiente que asigne un número a cada bola de forma que si \(B_1\), \(B_2\), …, \(B_n\) son bolas disjuntas contenidas en otra bola \(B\), entonces se tenga $$\mu(B)\ge \sum_{j=1}^n \mu(B_j).$$
Medidas doblantes.
En muchas ocasiones consideramos un espacio dotado de una distancia y una medida \((X,d,\mu)\). En el Análisis Matemático de la segunda mitad del siglo XX, se estudiaron muchas propiedades de estos espacios. Muchas pruebas usaban de la propiedad de que la medida de una bola crece con el radio \(r\) de manera proporcional a una potencia de \(r\). En particular para muchos espacios de medida \((X,d,\mu)\) hay una constante \(m\) tal que$$\mu(B(a,2r))\le m\;\mu(B(x,r)).$$
La medida de la bola de radio doble está controlada por la medida de la bola.
Diremos que la medida es doblante si tiene esta propiedad. Y la mejor (la más pequeña) constante \(m\) que pueda ponerse la denotamos por \(m=m(\mu)\).
El teorema de Soria y Tradacete.
La constante \(m\) de una medida doblante ha de ser siempre \(m\ge 1\) porque la bola de radio \(2r\) mide al menos lo mismo que la bola de radio \(r\). Puesto que estamos considerando espacios métricos arbitrarios y medidas doblantes cualesquiera pudiera parecer que no hay ninguna otra restricción sobre \(m\), pero Soria y Tradacete han conseguido probar que esto no es cierto y de una forma realmente sorprendente:
Teorema. Sea \((X,d,\mu)\) un espacio métrico dotado de una medida doblante \(\mu\), si \(X\) tiene al menos dos puntos, entonces \(m(\mu)\ge \frac{1+\sqrt{5}}{2}=\varphi\), la razón áurea.
Por simplificar un triplete \((X,d,\mu)\) formado por el espacio \(X\) de más de dos puntos, la distancia \(d\) y la medida doblante \(\mu\) lo denominaremos un espacio homogéneo.
La demostración es tan simple y elegante que no me resisto a incluirla para los interesados:
Hasta el trabajo de Soria y Tradacete se solía ver escrito: Sea \((X,d,\mu)\) un espacio métrico dotado de una medida doblante es decir para toda bola \(B(a,r)\) tenemos \(\mu(B(a,2r))\le m\mu(B(x,r))\) con \(m\ge1\). Se añadía la desigualdad obvia \(m\ge1\) pero nadie había reparado en que necesariamente era \(m\ge\varphi\). De hecho \(m=1\) ocurre en el espacio con un solo punto, pero nadie necesita estudiar este espacio para nada.
El problema de Soria y Tradacete.
Ahora viene lo que realmente me cautivó de este trabajo cuando lo vi en junio pasado. En el trabajo ellos determinan \(m(\mu)\) para muchas medidas doblantes y obtienen siempre que \(m(\mu)\ge2\), de manera que en junio formularon la cuestión siguiente:
Problema. ¿Existe o no un espacio homogéneo \((X,d,\mu)\) con \(2> m(\mu)\ge\varphi\)?
Para resolverlo debemos construir un espacio \(X\) dotarlo de una distancia \(d\) y una medida doblante, es decir, que exista una constante \(m\) con \(\varphi\le m<2\) y tal que para toda bola \(B(a,r)\) en el espacio se tenga $$\mu(B(a,2r))\le m\mu(B(x,r)).$$ O por el contrario probar que no existe tal espacio.
A lo largo del trabajo nos dan motivos para pensar que la respuesta va a ser negativa que si \((X,d,\mu)\) es un espacio homogéneo, entonces \(m\ge2\). Por tanto que la razón áurea no tiene realmente nada que ver en la cuestión.
Por ejemplo ellos ven que \(m\ge2\) si el espacio métrico \((X,d)\) cumple cualquiera de las condiciones siguientes:
- Si \(X\) tiene un punto aislado, es decir, hay una bola que se reduce a su centro.
- Si \(X\) es un conjunto finito.
- Si \(X\) contiene un arco, esto es la imagen continua y biyectiva de un segmento de \(\textbf{R}\).
- Si \(X\) es ultramétrico, una condición que cumplen muchos espacios que aparecen en Álgebra.
- Si \(X\) es completo.
Otros motivos para pensar que el problema es tratable.
Analicemos la prueba del teorema. Hay dos puntos \(a\) y \(b\) en el espacio a distancia \(r=d(a,b)>0\). Consideramos las siguientes bolas $$B(a,r/3), \ B(a,2r/3),\ B(a, 4r/3), B(b,r/3), \ B(b,2r/3),\ B(b, 4r/3).$$ Designemos sus medidas por \(a_{13}\), \(a_{23}\), \(a_{43}\) y \(b_{13}\), \(b_{23}\), \(b_{43}\). Todas son positivas por definición $$a_{13}>0, \ a_{23}>0,\ a_{43}>0, \ b_{13}>0, \ b_{23}>0,\ b_{43}>0.$$
Entre ellas se tiene por ser la medida doblante $$a_{23}\le m\; a_{13},\ a_{43}\le m\; a_{23},\ b_{23}\le m\; b_{13},\ b_{43}\le m\; b_{23},$$ además \(B(a,2r/3)\cap B(b,r/3)\subset B(a,4r/3)\) y \(B(b,2r/3)\cap B(a,r/3)\subset B(b,4r/3)\) y como las bolas en cada unión son disjuntas se tiene $$a_{23}+b_{13}\le a_{43}, \quad b_{23}+a_{13}\le b_{43}$$
La prueba viene a decir que estas desigualdades implican que \(m\ge\varphi\).
En mis clases suelo decir a mis alumnos que los programas hoy día nos potencian como matemáticos. No me resistí cuando leí la prueba en probar con Mathematica:
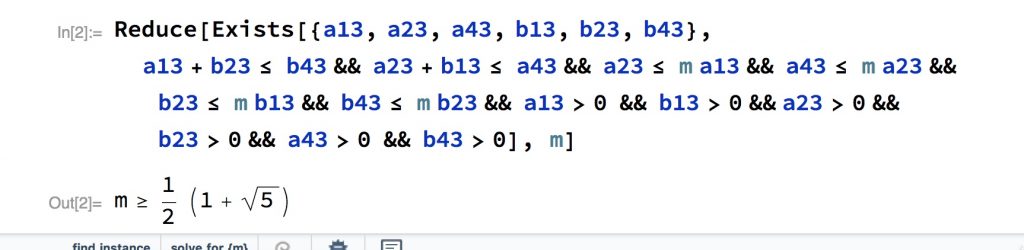
Lo que esto nos dice es que hay un algoritmo que dadas las desigualdades anteriores obtiene un enunciado equivalente eliminando las variables cuantificadas. Hay un teorema bastante sorprendente de Tarski y Seidenberg que dice que para cualquier expresión formada por ecuaciones polinómicas, desigualdades y conectivas lógicas, puede darse otra sin cuantificadores equivalente a ella. Es lo que ha efectuado el Mathematica con nuestra fórmula eliminando todas las variables cuantificadas y dejando solo una expresión en la única variable no cuantificada \(m\). De todos modos el algoritmo se complica enormemente con el número de variables y no resulta muy práctico en este caso al menos.
Soria y Tradacete añaden una nota al final de la prueba de su teorema:
Debemos notar que, a pesar de que aparentemente es irrelevante la elección de los radios de las bolas que hemos considerado en la prueba del teorema (esto es \(r/3\), \(2r/3\) y \(4r/3\)), cualquier otra combinación nos lleva a una estimación más débil.
La solución de la cuestión.
En febrero publican una nueva versión de su trabajo. Ya en junio ellos apuntan que la solución podría consistir en dado un espacio homogéneo \((X,d,\mu)\) tratar de construir en su completado \(\widehat{X}\) una medida doblante \(\widehat{\mu}\) que tenga una constante \(m(\widehat\mu)\le m(\mu)\). Puesto que todo espacio completo cumple \(m(\widehat\mu)\ge2\), podríamos deducir que la constante inicial \(m(\mu)\ge2\). A veces ocurre, uno tiene la solución pero no confía en ella suficientemente. En uno de los trabajos citados por ellos en la primera versión se construye esa medida \(\widehat{\mu}\) así que la construcción que ellos habían apuntado es suficiente para resolver el problema.
Esto parece acabar la cuestión. Sin embargo hay algo insatisfactorio en la prueba de que \(m(\mu)\ge2\). Es bastante complicada, sobre todo si uno la compara con la prueba de que \(m(\mu)\ge\frac{1+\sqrt{5}}{2}\). Uno tiene que aplicar la aditividad de la medida para \(n\) bolas disjuntas contenidas en otra bola, con \(n\) mayores que cualquier límite dado.
Esto se une a que cuando escribí la primera versión de esta entrada imaginé una posible demostración más directa del resultado. No me resisto a escribir mi problema, porque no usa apenas teoría, de manera que con las matemáticas del bachillerato se puede entender el enunciado. Podríamos de ese modo dar una prueba, probablemente más simple, del resultado \(m(\mu)\ge2\).
El problema elemental.
Volvamos a la idea de la prueba de \(m(\mu)\ge\frac{1+\sqrt{5}}{2}\), en ella se usan solo dos puntos. Sean \(a\) y \(b\) los puntos, sin perder generalidad podemos suponer que su distancia es \(d(a,b)=1\).
Razonamientos parecidos a los del teorema nos permiten deducir que la función $$f(x)=\frac12(\mu(B(a,x))+\mu(B(b,x)),\qquad x>0$$ cumple las siguientes condiciones:
- (a) \(f\) es monótona: si \(0<x<y\) entonces \(f(x)\le f(y)\).
- (b) \(f(2x)\le m f(x)\).
- (c) Para todo \(x>0\) es \(f(x)>0\).
- (d) Para todo \(0<x<1\), tenemos \(f(1-x)+f(x)\le f(1+x)\).
La función \(f(x)=x\) cumple todas estas condiciones con \(m=2\).
Si existiera una medida doblante con \(m(\mu)<2\), entonces existiría la \(f\colon(0,\infty)\to(0,\infty)\) cumpliendo las condiciones anteriores.
Luego nuestro problema es ahora:
Problema. ¿Existe \(f\colon(0,+\infty)\to(0,+\infty)\) satisfaciendo las condiciones (a), (b), (c) y (d) con un \(m\in [\varphi,2)\)?
No hay espacio métrico, no hay medida, no pido más que una función, no creo que esta pregunta dure mucho tiempo abierta …
Si existiera la función \(f\) cumpliendo las condiciones anteriores con una constante \(m\), entonces \(m\ge\varphi=\frac{1+\sqrt{5}}{2}\). La prueba es muy simple, tendríamos $$f(2/3)\le m\, f(1/3),\quad f(4/3)\le m\, f(2/3),\quad f(1/3)+f(2/3)\le f(4/3).$$
Luego sucesivamente deducimos que
\begin{gather*}f(1/3)+f(2/3)\le f(4/3)\\f(1/3)+f(2/3)\le m\;f(2/3)\\f(1/3)\le (m-1) f(2/3)\\f(1/3)\le (m-1)m\, f(1/3)\\m(m-1)\ge1\\m^2-m-1=\bigl(m-\tfrac{1+\sqrt{5}}{2}\,\bigr)\bigl(m-\tfrac{1-\sqrt{5}}{2}\,\bigr)\ge0\end{gather*}
Como \(m>0\) esto solo puede ser cierto si \(m\ge\frac{1+\sqrt{5}}{2}\).
Espero que algún lector pueda probar que no existe ninguna \(f\) cumpliendo estas condiciones con \(m<2\), eso probaría que la constante de las medidas doblantes es \(\ge2\), con una prueba que presumiblemente será más simple que la de Soria y Tradacete.
Para saber más.
El trabajo original en arXiv es fácil de leer:
Javier Soria y Pedro Tradacete, The least doubling constant of a metric measure space, arXiv:1806.06758, dos versiones.
Hay poco más que añadir, el problema lo han planteado ellos. Los conceptos básicos de medidas y espacios métricos son fáciles de encontrar en libros de análisis.


Dejar una contestacion