Construcción geométrica de Pi

Delantal:

Para conmemorar que el Día de Pi se aproxima proponemos un problema sobre una construcción geométrica del mismo. Recordamos que un número es algebraico si es una raíz de un polinomio con coeficientes enteros; en caso contrario, se dice trascendente. Los números trascendentes y los algebraicos viven en un equilibrio paradójico que se empeña en revelar nuestra ignorancia: casi todos los números son trascendentes, pero se conocen muy pocos. Uno de ellos es el número \(\pi\). Lindemann demostró en 1882 que \(\pi\) es trascendente, dando respuesta negativa al problema de la cuadratura del círculo, pues los números que se pueden construir con regla y compás (en un número finito de pasos) son algebraicos. En el Divertimento de hoy describimos una construcción geométrica de Th. Osler en la que se obtiene el número \(\pi\) tras una cantidad infinita de pasos.

Divertimento:

Justificar la siguiente construcción:

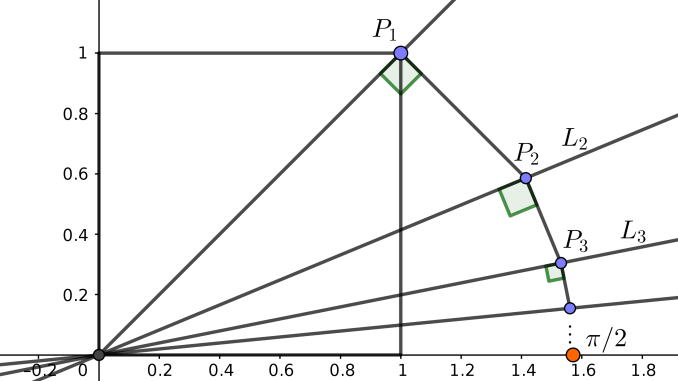
1. Se traza el cuadrado unidad y la diagonal \(L_1\) que pasa por el origen y por el vértice \(P_1\) .

2. Se traza la bisectriz \(L_2\) del ángulo que forma \(L_1\) con el eje \(x\). Se traza la perpendicular a \(L_1\) por \(P_1\), que corta a dicha bisectriz en el punto \(P_2\).

3. Se reitera el proceso: se traza la bisectriz \(L_3\) del ángulo que forma \(L_2\) con el eje \(x\) y se traza la perpendicular por \(P_2\), que corta a \(L_3\) en el punto \(P_3\). Así sucesivamente.

4. La sucesión de las longitudes de los segmentos converge a \(\pi/2\).

Indicación: damos por válida la siguiente fórmula de Viète:

$$\frac{2}{\pi} = \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2}}}} \cdots$$

Soluciones:

Envía tus soluciones, antes del domingo 17 de marzo, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el miércoles 20 de marzo. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.