Solución: Construcción geométrica de Pi

Publicamos la solución al Divertimento Construcción geométrica de Pi. Alberto Castaño y Cristóbal Sanchez-Rubio han enviado soluciones al problema utilizando la fórmula de Viète y con una fórmula alternativa.

El problema está extraído de un artículo de Thomas Osler.

Divertimento:

Justificar la siguiente construcción:

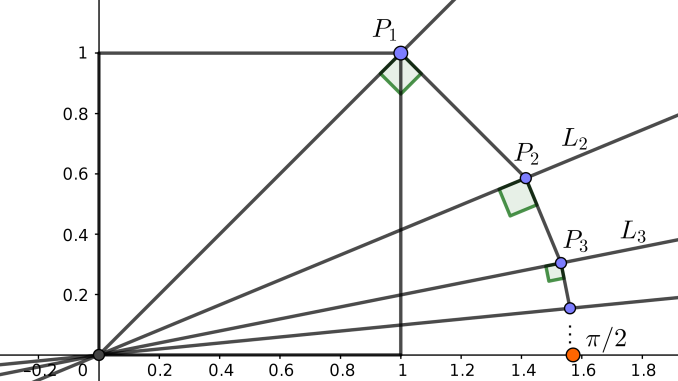
1. Se traza el cuadrado unidad y la diagonal \(L_1\) que pasa por el origen y por el vértice \(P_1\) .

2. Se traza la bisectriz \(L_2\) del ángulo que forma \(L_1\) con el eje \(x\). Se traza la perpendicular a \(L_1\) por \(P_1\), que corta a dicha bisectriz en el punto \(P_2\).

3. Se reitera el proceso: se traza la bisectriz \(L_3\) del ángulo que forma \(L_2\) con el eje \(x\) y se traza la perpendicular por \(P_2\), que corta a \(L_3\) en el punto \(P_3\). Así sucesivamente.

4. La sucesión de las longitudes de los segmentos converge a \(\pi/2\).

Indicación: damos por válida la siguiente fórmula de Viète:

$$\frac{2}{\pi} = \sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2} + \frac{1}{2}  \sqrt{\frac{1}{2}}}} \cdots$$

Solución:

Solución propuesta por Alberto Castaño.

Sea \(l_1=\sqrt{2}\) la distancia de la diagonal del cuadrado, \(OP_1\), y sea \(P_0\) el punto \((0,1)\). Así, sabemos que \(c_1:=\cos(\widehat{P_0OP_1})=\cos(\pi/4)=1/\sqrt{2}\).

Probemos ahora por inducción que $$(*) \qquad l_n:=OP_n=\left(\prod_{i=1}^nc_i\right)^{-1},$$ donde los \(c_i\) se construyen recursivamente como $$c_k=\sqrt{\frac{1}{2}+\frac{1}{2}c_{k-1}},$$ siendo \(c_1=1/\sqrt{2}\) como arriba.

En primer lugar debemos darnos cuenta de que \(c_n=\cos(\pi/2^{n+1})\). En efecto, si \(n=1\) es cierto, y para un \(k\) arbitrario, suponiéndolo cierto para \(c_{k-1}\), tenemos que $$ c_k=\sqrt{\frac{1+c_{k-1}}{2}}=\sqrt{\frac{1+\cos(\pi/2^k)}{2}}=\cos(\pi/2^{k+1}),$$ por la fórmula del coseno del ángulo medio.

Tomemos ahora un \(r\) arbitrario y supongamos cierta la fórmula (*) para \(l_{r-1}\). Como el triángulo \(OP_{n-1}P_n\) es rectángulo, podemos expresar \(l_r=OP_r\) como $$ l_{r-1}\cos(\widehat{P_{r-1}OP_r}).$$ Ahora bien, \(\widehat{P_{r-1}OP_r}=\pi/2^{r+1}\), con lo que $$l_r=\left(\prod_{i=1}^{r-1}c_i\right)^{-1}c_r^{-1}.$$

En conclusión, cuando repetimos indefinidamente este proceso, llegamos a que $$\lim_{n\rightarrow\infty}l_n=\left(\prod_{i=1}^\infty c_i\right)^{-1}=(2/\pi)^{-1}=\pi/2.$$

Solución propuesta por Cristóbal Sánchez-Rubio.

Llamando \(a_k\) la longitud del segmento \(OP_k\), tenemos $$\frac{a_{k-1}}{a_k} = \cos \frac{\pi}{2^{k+1}},$$ y como \(a_1 = \sqrt{2}\), se sigue que $$\displaystyle a_k = \frac{\sqrt{2}}{\prod_{n=2}^k \cos \frac{\pi}{2^{n+1}}}.$$ Para calcular $$\prod_{n=2}^\infty \cos \frac{\pi}{2^{n+1}}$$ usaremos la ecuación descubierta por Euler $$\sin x = x \prod_{n=1}^\infty \cos \frac{x}{2^n}.$$ Esta fórmula se puede encontrar en el libro Trigonometric Delights de Eli Maor. Haciendo \(x=\pi/2\), queda $$1 = \frac{\pi}{2} \prod_{n=1}^\infty \cos \frac{\pi}{2^{n+1}}=\frac{\pi}{2} \cos \frac{\pi}{4} \prod_{n=2}^\infty \cos \frac{\pi}{2^{n+1}},$$ de donde $$\prod_{n=2}^\infty \cos \frac{\pi}{2^{n+1}} = \frac{4}{\pi \sqrt{2}}.$$ De aquí $$\lim_{n \to \infty} a_n = \frac{\pi \sqrt{2}\sqrt{2}}{4} = \frac{\pi}{2}.$$