Paralogismo II

Delantal:

Hace algún tiempo propusimos un paralogismo o falso razonamiento para mantener despiertos y desconfiados a nuestros seguidores. Repetimos la experiencia solicitando que nos ayuden a seguir creyendo que existen triángulos con tres lados de diferente longitud.

Divertimento:

Teorema. Todo triángulo es isósceles.

Demostración. Sea \(ABC\) un triángulo cualquiera. Si la bisectriz de \(B\) es perpendicular a \(AC\), el triángulo es isósceles. Si no lo es, esta bisectriz se cortará con la mediatriz de \(AC\) en un punto \(I\). Por este punto \(I\) se trazan las perpendiculares \(IE\) y \(IF\) a los lados \(BA\) y \(BC\) respectivamente y las rectas \(IA\) y \(IC\).

Los triángulos rectángulos \(BEI\) y \(BFI\) son iguales (rectángulos, con un ángulo agudo igual y la hipotenusa común); de modo que \(BE=BF\). Los triángulos rectángulos \(AEI\) y \(CFI\) son iguales (rectángulos con un cateto y la hipotenusa iguales); de modo que \(EA=FC\). Sumando estas igualdades resulta \(BA=BC\), es decir que el triángulo es isósceles.

Análogo razonamiento sigue si el punto es exterior.

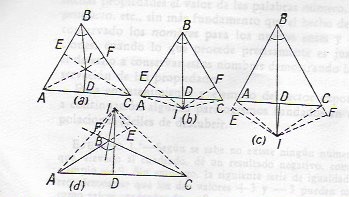
¿Dónde está el error?

Soluciones:

Envía tus soluciones, antes del domingo 5 de mayo, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el miércoles 8 de abril. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.