Solución: Paralogismo II

Publicamos la solución al divertimento Paralogismo II. Gracias a Cristóbal Sánchez-Rubio y a Jaime Benabent por las soluciones que nos han enviado.

Divertimento:

Encuentra el error en la prueba del siguiente resultado.

Teorema. Todo triángulo es isósceles.

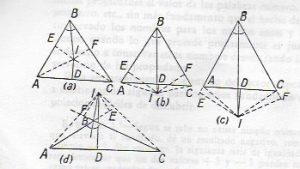
Demostración. Sea \(ABC\) un triángulo cualquiera. Si la bisectriz de \(B\) es perpendicular a \(AC\), el triángulo es isósceles. Si no lo es, esta bisectriz se cortará con la mediatriz de \(AC\) en un punto \(I\). Por este punto \(I\) se trazan las perpendiculares \(IE\) y \(IF\) a los lados \(BA\) y \(BC\) respectivamente y las rectas \(IA\) y \(IC\).

Los triángulos rectángulos \(BEI\) y \(BFI\) son iguales (rectángulos, con un ángulo agudo igual y la hipotenusa común); de modo que \(BE=BF\). Los triángulos rectángulos \(AEI\) y \(CFI\) son iguales (rectángulos con un cateto y la hipotenusa iguales); de modo que \(EA=FC\). Sumando estas igualdades resulta \(BA=BC\), es decir que el triángulo es isósceles.

Análogo razonamiento sigue si el punto es exterior.

Solución:

Solución propuesta por Cristóbal Sánchez-Rubio.

Las figuras mostradas en la demostración son falsas.

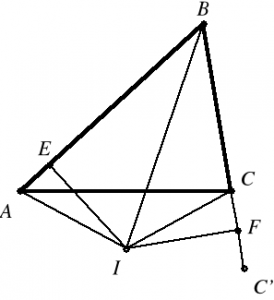
Supongamos un triángulo con \(BA>BC\). Como \(A\) y \(F\) son simétricos respecto de la bisectriz, si \(E\) está en el interior del segmento \(AE\), el punto \(F\) debe estar en la prolongación del lado \(BC\) con \(EA=CF\) (en lugar de \(EA=FC\)).

Trasladando \(F\) con el vector \(CF\), obtenemos \(C’\). Si ahora sumamos, obtenemos \(BE+EA=BF+CF\), que es equivalente a \(BA=BC’\). La conclusión correcta es que el triángulo \(BAC’\) sí es isósceles.

Resumiendo: el fallo consiste que los segmentos que se usan son orientados y al no tenerlo en cuenta se da por buena la igualdad \(EA=FC\) cuando debería ser \(EA=-FC\).

El razonamiento vale para las demás configuraciones.