James Dean, atascos en Sao Paulo y la ecuación de Burgers

El tráfico: catástrofes, molestias y modelos

Tal vez, el accidente más famoso de la Historia se produjo el 30 de Septiembre de 1955 en Cholame (California, EEUU). Aquel día murió James Dean, un actor de 24 años, que poco antes había logrado ser mundialmente célebre con sólo tres films.

 

Dean era un gran aficionado a la velocidad. Cuando murió viajaba a la localidad de Salinas, cercana a San Francisco, para participar en una carrera con su bólido (un Porsche Spyder 550, bautizado como «Little Bastard»). Sin embargo, según parece, no iba demasiado rápido. De hecho, el accidente ni siquiera fue culpa suya: un joven estudiante de 23 años que conducía un Ford Custom Tudor lo provocó al saltarse un Ceda el Paso en un cruce de la ruta 466.

El tráfico genera de vez en cuando catástrofes. Todos tenemos en nuestra mente decenas (tal vez cientos) de desgraciados accidentes, a veces debidos a la imprudencia del conductor, pero en otras ocasiones claramente involuntarios e incluso inevitables.

 

Los atascos constituyen otro gran problema del tráfico. La causa fundamental de un atasco es el exceso de vehículos. Por ejemplo, en una autovía de dos carriles por sentido, la capacidad máxima es de unos 4000 vehículos por hora. A medida que el flujo se va acercando a esta cantidad, las velocidades de los vehículos disminuyen, unos y otros se acercan y, al frenar, las posibilidades de un atasco crecen.

Recomiendo vivamente al lector la lectura del artículo [1], donde quedan descritos los cinco atascos más famosos (y desastrosos) de la Historia. En particular, merece la pena mencionar dos de ellos:

• El que se produjo en Sao Paulo (Brasil) el 23 de mayo de 2014, que alcanzó el récord histórico de 344 km de atascos acumulados simultáneamente alrededor de la ciudad.

• El que tuvo lugar en China, en la autopista G110 de Pekín al Tíbet, de «sólo» 100 km de longitud, que tuvo una duración de … ¡11 días!

 

Existen técnicas matemáticas que permiten modelar con precisión el tráfico bajo múltiples circunstancias. Véase por ejemplo [2], donde los autores presentan varias propuestas de control predictivo para la regulación del tráfico que incorporan límites variables de velocidad en situaciones realistas. En particular, técnicas  de este tipo, adaptadas a la ronda periférica de Grenoble (Francia), conducen a recomendaciones útiles: la velocidad máxima en cada momento, la frecuencia de acceso, el uso del carril reversible, etc.

Una ecuación para el tráfico

Consideraremos a continuación una situación muy simple (en realidad, la más sencilla posible), donde pretendemos calcular la densidad de tráfico \(\rho = \rho(x,t)\) en una vía de una única dirección (digamos de izquierda a derecha) que ocupa los puntos \(x\), con \(0 < x < L\), en los instantes de tiempo \(t\), con \(0 < t < T\).

La densidad \(\rho\) determina el flujo de tráfico \(F\) y la velocidad de éste \(V\). Con frecuencia, se suele suponer que
$$
F = V \rho – D \rho_x, \quad V = \frac{V_{\rm max}}{\rho_{\rm max}}\left(\rho_{\rm max} – \rho\right),
$$
donde \(D > 0\) y \(V_{\rm max}\) y \(\rho_{\rm max}\) son valores máximos posibles para la velocidad y la densidad. Aquí y en lo que sigue, los subíndices denotan derivadas parciales.

 

Todo esto tiene mucho sentido. Por una parte, el flujo es una cantidad positiva, igual al producto de la velocidad por la densidad, al que hay que restar otra cantidad positiva, proporcional a la derivada espacial de \(\rho\) (esto es, a la variación de esta función respecto de la variable \(x\); se puede interpretar \(D \rho_x\) como un término de fricción). Por otra, decimos que la velocidad es nula cuando la densidad alcanza un valor máximo y crece linealmente hacia un valor máximo cuando \(\rho\) tiende a cero.

Teniendo en cuenta que, en todo intervalo \(a < x < b\), el cambio en tiempo de la densidad debe coincidir con el número de vehículos que entran por \(x = a\) menos el número de los que salen por \(x = b\), se llega fácilmente a la ecuación que debe verificar \(\rho\):
$$
\rho_t + \left( \frac{V_{\rm max}}{\rho_{\rm max}}\left(\rho_{\rm max} – \rho\right) \rho \right)_x = D \rho_{xx} .
\quad\qquad\qquad\qquad\ \ \ \ (1)
$$

Generalmente, se suele completar esta ecuación con información sobre el comportamiento de \(\rho\) en los extremos \(x = 0\) y \(x = L\) de la vía y sobre el estado inicial de \(\rho\), esto es, sus valores para \(t = 0\):
$$
\begin{array}{c}
\rho(0,t) = u(t), \ \ \rho_x(L,t) = 0, \ \text{ para } \ 0 < t < T, \\
\rho(x,0) = \rho_0(x), \ \text{ para } \ 0 < x < L,
\end{array}
\qquad\qquad(2)
$$

La primera tarea matemática es, en consecuencia, la siguiente: dados \(\rho_0\) y \(u\), calcular la solución de \((1)\)-\((2)\).

Un experimento numérico

 

Para la resolución de \((1)\)-\((2)\), se ha usado un método numérico que reposa sobre las ideas siguientes:

1. En primer lugar, se aproximan las derivadas espaciales por cocientes en diferencias en un conjunto adecuado de puntos \(x_i\), con \(1 \leq i \leq m\). Esto permite sustituir la ecuación en derivadas parciales \((1)\) por un sistema diferencial ordinario no lineal de dimensión aproximadamente igual a un número reducido de veces \(m\).

2. A continuación, se usa un método de Runge-Kutta de alto orden para la resolución del sistema resultante.

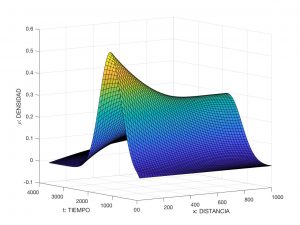
En la Figura 5, se ha visualizado (una aproximación numérica de) la solución del problema precedente para
$$
\begin{array}{c}
L = 10^3~m, \quad T = 3.6 \times 10^3~s \ \ (10~h), \quad V_{\rm max} = L/T = 27.778~m/s \ \ (100~km/h), \\
\rho_{\rm max} = 0.555~veh/s \ \ (2000~veh/h), \quad D = 4 \times 10^4~m^2/s, \\
\rho_0(x) = 0, \quad u(t) = \rho_{\rm max} e^{-|t – T/5|^2/(2 \sigma^2)} \ \text{ con } \ \sigma = \sqrt{0.015}~s.
\end{array}
$$

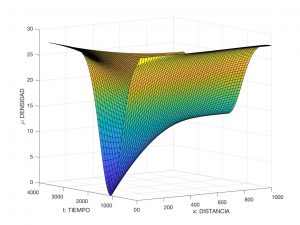
Se presenta por otra parte la distribución de velocidades en la Figura 6.

 

La ecuación de Burgers

Con sencillos cambios de variables, es posible re-escribir \((1)\) de manera mucho más simple. Así, cambiando las variables \(x\), \(t\), \(\rho\) respectivamente por
$$
\tilde x := x/L, \quad \tilde t := t/T, \quad \tilde \rho := \rho/\rho_{\rm max}.
$$

Volviendo a denotar \(x\), \(t\), \(\rho\) las nuevas variables, obtenemos la nueva ecuación
$$
\rho_t + \left(\left(1 – \rho\right) \rho \right)_x = \nu \rho_{xx} ,
$$

 

donde \(\nu := D/(L V_{\rm max})\). Ahora, poniendo \(z := 2\rho -1\), obtenemos para \(z\) la llamada ecuación de Burgers (también conocida como ecuación de Bateman-Burgers):
$$
z_t + z z_x = \nu z_{xx} .
$$

Esta ecuación aparece de hecho en varias áreas de la Matemática Aplicada, relacionadas con la mecánica de fluidos [3], la acústica no lineal [4], la dinámica de gases, etc. Fue introducida por el matemático inglés Harry Bateman en 1915 (véase [5]) y posteriormente estudiada por el físico holandés Johannes (Jan) Martinus Burgers en 1948 (véase [6]).

Para saber más

1. Ver: https://motor.elpais.com/actualidad/los-5-atascos-mas-monumentales-historia, https://col2.com/el-accidente-de-james-dean.
2. Domínguez Frejo, J.R.; Núñez Vicencio, A.; De~Schutter, B.; Fernández Camacho, E. – Hybrid model predictive control for freeway traffic using discrete speed limit signals, Transportation Research Part C, vol. 46, pp. 309-325, Sept. 2014.
3. Landajuela, M. – Burgers equation, BCAM, 2011. Ver: https://www.bcamath.org/projects/NUMERIWAVES/Burgers_Equation_M_Landajuela.pdf.
4. Hamilton, M.F.; Blackstock, D.T. – Nonlinear Acoustics, Academic Press, 1998.
5. Bateman, H. – Some recent researches on the motion of fluids, Monthly Weather Review, 43(4), 163–170, 1915.
6. Burgers, J. M. – A mathematical model illustrating the theory of turbulence, En «Advances in applied mechanics», Vol. 1, pp. 171-199, Elsevier, 1948.