Algunas demostraciones matemáticas nos sorprenden por que la prueba sigue un camino inesperado. Eso es lo que ocurre con la prueba por Wiles del último Teorema de Fermat. Hoy traigo otro problema, mucho más asequible que el último Teorema de Fermat, pero que también comparte una prueba sorprendente. Lo puedo contar pues sin conocer esa prueba estuve un tiempo tratando de probar el resultado.
Para mí todo comienza cuando vi un misterioso problema propuesto por el padre de la Matemática Experimental Jonathan Borwein quién, junto con David H. Bailey, proponen la igualdad
\begin{multline}\frac{24}{7\sqrt{7}}\int_{\pi/3}^{\pi/2}\log\Bigl|\frac{\tan t+\sqrt{7}}{\tan t-\sqrt{7}}\Bigr|\,dt\stackrel{?}{=}\\\sum_{n=0}^\infty \Bigl\{\frac{1}{(7n+1)^2}+\frac{1}{(7n+2)^2}-\frac{1}{(7n+3)^2}+\frac{1}{(7n+4)^2}-\frac{1}{(7n+5)^2}-\frac{1}{(7n+6)^2}\Bigr\}.\end{multline}
y continuan: Esta identidad ha sido verificada con 5000 cifras decimales, pero no tenemos una prueba. Surge del volumen de un tetraedro ideal en el espacio hiperbólico. Por motivos de topología algebraica se sabe que la razón entre el miembro izquierdo y el derecho es un número racional.
Por simplificar escribiremos la igualdad anterior como \(I\stackrel{?}{=} S\), representando por \(I\) a la integral y por \(S\) a la serie. Desde que vi planteado el problema me gustó. El tema promete, no se me escapaba entonces que la serie puede ser escrita en la forma $$S=\sum_{n=1}^\infty \frac{\chi(n)}{n^2},$$ donde \(\chi(n)\) vale en cada caso \(1\), \(0\) o \(-1\). \(\chi(n)\) es lo que se llama un carácter de Dirichlet. Es una función multiplicativa: \(\chi(nm)=\chi(n)\chi(m)\), de forma que $$L(s)=\sum_{n=1}^\infty\frac{\chi(n)}{n^s}$$ tiene numerosas propiedades en común con la función \(\zeta(s)\) de Riemann. En particular se conjetura que sus ceros \(L(\rho)=0\) o son enteros negativos, o bien están situados en la recta crítica \(\Re s=\frac12\). Dirichlet usó esta función para probar que si \(a\) es primo con \(b\) hay infinitos primos de la forma \(a+nb\).
Por tanto la igualdad es ahora $$\frac{24}{7\sqrt{7}}\int_{\pi/3}^{\pi/2}\log\Bigl|\frac{\tan t+\sqrt{7}}{\tan t-\sqrt{7}}\Bigr|\,dt\stackrel{?}{=}L(2).$$ Aquí la función \(L(s)\) esta asociada a la extensión cuadrática \(\mathbf Q(\sqrt{-7})\) de \(\mathbf Q\). Es evidente que el número \(7\) figura prominentemente en los dos miembros de la igualdad.
Borwein y Broadhurst.
¿Cuál es el origen del problema? Probablemente su origen está en un trabajo anterior:
Borwein, J. M. & Broadhurst D. J., Determination of rational Dedekind-zeta invariants of hyperbolic manifolds and Feynman knots and links, arXiv:hep-th/9811173 (1998).
En él Borwein y Broadhurst experimentan. Calculan el volumen de variedades \(\mathcal M\) de dimensión 3 dotadas de una geometría hiperbólica completa, y, por otro lado, el valor de la función zeta \(\zeta_K(2)\) para extensiones algebraicas \(K\) de \(\textbf Q\) con discriminante \(D\) y grado \(n\). Buscan y encuentran numerosas relaciones del tipo $$\frac{a}{b}\mathop{\rm vol}(\mathcal M)=\frac{(-D)^{3/2}}{(2\pi)^{2n-4}}\frac{\zeta_K(2)}{\zeta(2)},$$ donde \(a/b\) es un número racional. Ellos aclaran que iniciaron esta búsqueda siguiendo la petición de Don Zagier que sospechaba la existencia de estas relaciones entre volúmenes hiperbólicos y la función zeta de Dedekind. Don Zagier quería ejemplos para obtener conjeturas fundadas sobre estas relaciones.
En particular Borwein y Broadhurst encuentran experimentalmente la relación $$4 D\Bigl(\frac{3+i\sqrt{7}}{4}\Bigr)+2D\Bigl(\frac{3+i\sqrt{7}}{8}\Bigr)\stackrel{?}{=}7 D\Bigl(2\frac{1+i\tan\frac{\pi}{7}}{3-\tan^2\frac{\pi}{7}}\Bigr),$$ donde \(D(z)\) es la función de Bloch-Wigner. No es difícil ver que el segundo miembro es igual a \(\frac{7\sqrt{7}}{4}S\) y que el primer miembro está relacionado con \(I\) de forma que la igualdad es equivalente a \(I\stackrel{?}{=}S\).
La función de Bloch-Wigner.
Hemos visto que \(S\) tiene una interpretación aritmética. Lo que nos queda por ver es que \(I\) tiene una interpretación geométrica.
Es conveniente considerar el modelo de la geometría hiperbólica cuyos puntos se identifican con \(\textbf{C}\times(0,+\infty)\). Las rectas de la geometría son rectas o circunferencias perpendiculares al plano base \(\textbf{C}:=\textbf{C}\times\{0\}\) que representa los puntos del infinito y que podemos identificar con el plano complejo \(\textbf{C}\). Los planos de la geometría hiperbólica son los planos o superficies esféricas perpendiculares al plano base \(\textbf{C}\).
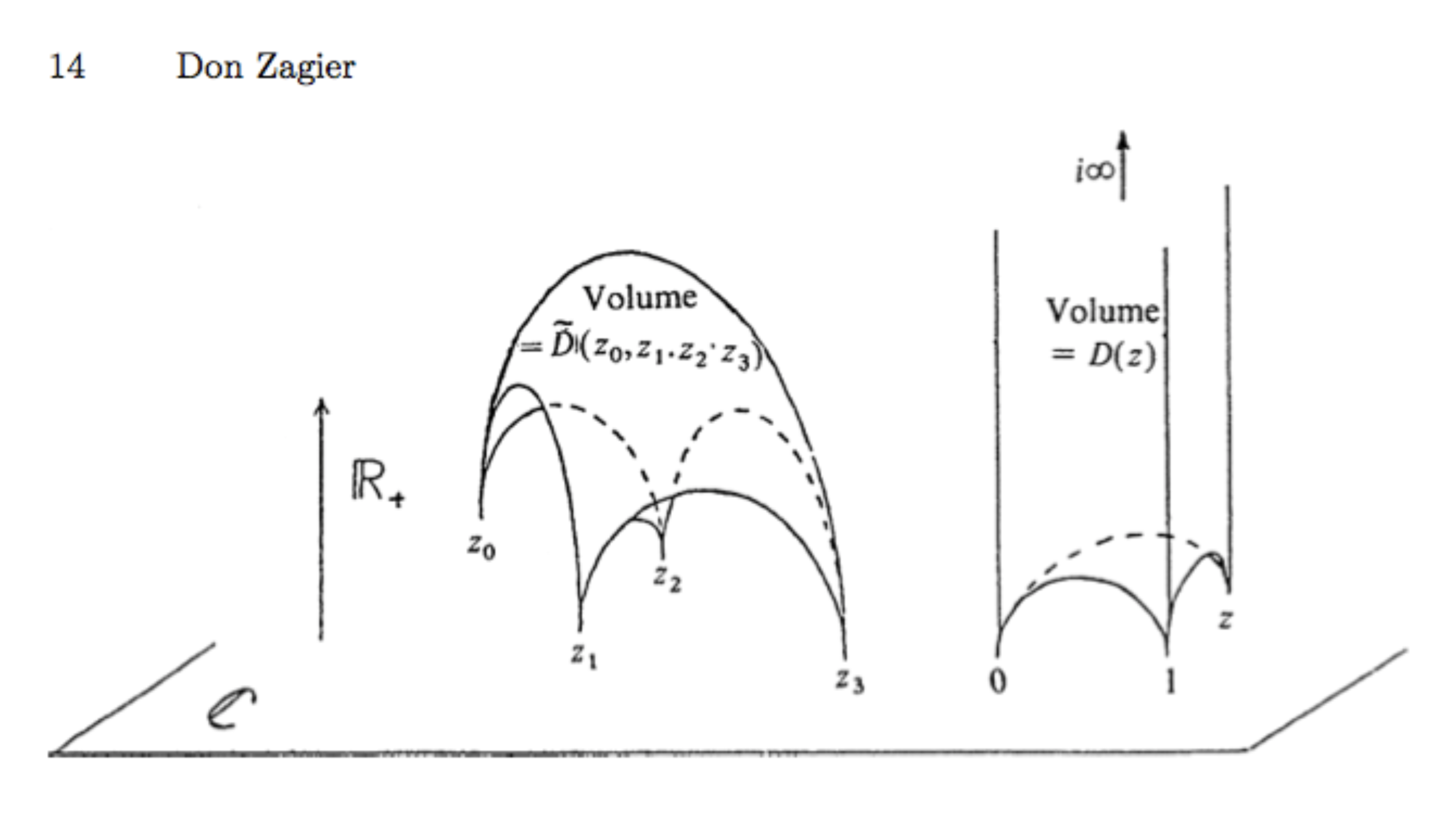
Se dice que un tetraedro (en la geometría hiperbólica) es ideal si sus vertices están en el infinito. \(D(z)\) es el volumen (hiperbólico) de un tetraedro ideal de vértices \((0,1,z, i\infty)\). Es una función a valores reales positivos definida en el plano complejo y vale \(0\) para \(z=0\), \(1\) o \(\infty\).
Para conocer la naturaleza de la función de Bloch-Wigner \(D(z)\), comenzamos con la función logaritmo integral $$\text{Li}_2(z)=\sum_{n=1}^\infty \frac{z^n}{n^2}=\int_0^z\log(1-t)\frac{dt}{t}.$$ La primera expresión es sólo válida para \(|z|<1\), en la segunda se integra a lo largo del segmento que une \(0\) y \(z\), siempre que el segmento no contenga a \(1\). Esta función es multivaluada y verifica muchas relaciones funcionales complicadas. Curiosamente esas relaciones se simplifican enormemente si consideramos la función modificada \(D(z)\) $$D(z)=\text{Im }\text{Li}_2(z)+\arg(1-z)\log|z|.$$ La función \(D(z)\) toma valores reales y es real analítica en todo \(\textbf{C}\) excepto en los puntos \(z=0\) y \(z=1\) en que no es real analítica, pero sí que es continua.
\(D\) se reduce en realidad a una función de una sola variable real si tenemos en cuenta que $$D(z)=\frac12\Bigl[D\Bigl(\frac{z}{\overline{z}}\Bigr)+D\Bigl(\frac{1-1/z}{1-1/\overline{z}}\Bigr)+D\Bigl(\frac{1/(1-z)}{1/(1-\overline{z})}\Bigr)\Bigr]$$ todos números de módulo unidad y combinamos con $$D(e^{i\theta})=\sum_{n=1}^\infty\frac{\sin n\theta}{n^2}.$$
Entre las propiedades de la función de Bloch-Wigner destaquemos las siguientes que jugarán un papel importante más tarde. Para todo \(z\in \textbf{C}\) tenemos $$D(z)+D(z^{-1})=D(z)+D(1-z)=0$$ y para dos números complejos cualesquiera \(z\), \(w\in \textbf{C}\) tenemos $$D(z)+D(w)+D\Bigl(\frac{1-z}{1-zw}\Bigr)+D(1-zw)+D\Bigl(\frac{1-w}{1-zw}\Bigr)=0.$$
La demostración de Zagier.
El problema de Borwein y Bailey tuvo su máxima publicidad en 2004 y 2005, sin embargo su solución está contenida en un trabajo de Zagier Hyperbolic manifolds and special values of Dedekind zeta-functions, publicado en 1986.
Sea \(K=\textbf{Q}(\sqrt{-d})\) un cuerpo cuadrático imaginario de discriminante \(d\), \(O_K\) el anillo de los enteros de \(K\). El grupo \(\text{SL}_2(O_K)\) de las matrices con términos en \(O_K\) y con determinante \(1\) actúa en el espacio hiperbólico tridimensional \(H^3=\textbf{C}\times(0,\infty)\) y Humbert en 1919 probó que $$\zeta_K(2)=\frac{4\pi^2}{d\sqrt{d}}\text{Vol}(H^3/\text{SL}_2(O_K)).$$
Esta es la conexión con la geometría, en un lado de la igualdad tenemos la función zeta de un cuerpo cuadrático en el otro el volumen de una variedad 3-dimensional completa con geometría hiperbólica.
Cualquier variedad hiperbólica 3-dimensional puede ser triangulada, y así descomponer su volumen en la suma de volúmenes de tetraedros. Aplicando esto a la variedad hiperbólica \(H^3/\text{SL}_2(O_K)\) podemos expresar esta como una suma de tetraedros. De hecho podemos reducirlo a una suma o diferencia de tetraedros ideales y el volumen será una combinación de valores \(D(z)\) siendo \(z\) vértices.
Interviene aquí un elemento insospechado: Una de las ideas de William Thurston es la geometrización. Las ideas de Thurston fueron probadas finalmente por Perelman en el año 2003, lo que de paso probaba la famosa Conjetura de Poincaré, que le valió la medalla Fields y el primer premio del milenio de un millón de dólares que, para sorpresa de muchos, rechazó.

La conjetura de geometrización afirma que cualquier variedad tridimensional puede dotarse de una geometría (o se descompone en piezas que admiten la geometrización). Thurston la fundaba en numerosos ejemplos. Los más impactantes se forman si tenemos un nudo o varias curvas cerradas enlazadas en \(\textbf{R}^3\), el complemento es una variedad, que Thurston descomponía en tetraedros para darles una geometría hiperbólica. Un caso particular de los estudiados por Thurston es el de los anillos de Borromeo.
El complemento de los anillos (tres circunferencias enlazadas como en la figura) es una variedad \(\mathcal M\), Thurston consigue describir esta variedad como una unión de tetraedros, y de ese modo lo dota de una geometría hiperbólica que cumple $$\text{Vol}(\mathcal M)=6\text{Vol}(H^3/\text{SL}_2(O_K))$$ y por otro lado Thurston consigue expresar este volumen como $$\text{Vol}(\mathcal M)=2\Bigl[2D\Bigl(\frac{3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1-i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1+i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)\Bigr].$$ Para \(K=\textbf{Q}(\sqrt{-7})\) tenemos \(\zeta_K(s)=\zeta(s)L(s)\), De manera que el resultado de Humbert puede escribirse $$L(2)=\sum_{n=1}^\infty\frac{\chi(n)}{n^2}=\frac{24}{7\sqrt{7}}\text{Vol}(H^3/\text{SL}_2(O_K))$$ o bien $$\sum_{n=1}^\infty\frac{\chi(n)}{n^2}=\frac{8}{21\sqrt{7}}\Bigl[2D\Bigl(\frac{3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1-i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)+D\Bigl(\frac{-1+i\sqrt{3}}{2}\cdot\frac{-3+i\sqrt{7}}{4}\Bigr)\Bigr]$$
La demostración tiene dos componentes difíciles de entender. La prueba de la fórmula de Humbert y la vision geométrica de Thurston sobre la composición de la variedad hiperbólica.
Más allá de la prueba.
La demostración de la igualdad \(I=S\) no es el final sino el principio de la verdadera cuestión.
Las funciones \(L(s)\) fueron introducidas por Dirichlet con objeto de probar que si \(a\) y \(b\) son dos números naturales primos entre sí, entonces hay infinitos primos de la forma \(p=an+b\). Dedekind más tarde asoció a cada extensión finita \(K\) del cuerpo de los números racionales \(\textbf{Q}\) una función zeta \(\zeta_K(s)\). Esta función tiene un polo simple en \(s=1\). El valor del residuo de la función $$\text{Res}_{s=1}\zeta_K(s)=\frac{h 2^{r_1}(2\pi)^{r_2}R}{w\sqrt{d}}$$ es una combinación de los invariantes más importantes del cuerpo \(K\). Podemos decir que conocemos el sentido del valor de la función zeta en \(s=1\). El trabajo de Zagier en 1986 es un intento de extender esto para \(\zeta_K(2)\). Esto completa el trabajo de Humbert que consideraba el caso de ser \(K\) una extensión cuadrática. Zagier prueba que en el caso general $$\zeta_K(2)=\frac{\pi^{2r_1+2r_2}}{\sqrt{|d|}}\times\sum_\nu c_\nu A(x_{\nu,1})\cdots A(x_{\nu,r_2})\qquad \text{suma finita}$$ donde \(c_\nu\) son números racionales, los \(x_{\nu,j}\) son números reales algebraicos y \(A(x)\) es una función relacionada con \(D(x)\).
Zagier ha ido refinando este resultado. En un trabajo con Herbert Gangl prueba un resultado mucho más preciso:
Teorema. Sea \(K\) un cuerpo algebraico con \(r_1\) inmersiones reales y \(r_2\) complejas. Tenemos
(1) El grupo de Bloch \(\mathcal B(K)\) es finitamente generado de rango \(r_2\).
(2) Sea \(\xi_1\), … \(\xi_{r_2}\) una \(\textbf{Q}\)-base de \(\mathcal B(K)\times\textbf{Q}\) y \(\sigma_1\), …, \(\sigma_{r_2}\) un conjunto de inmersiones complejas (que no contiene a dos complejas conjugadas) de \(K\) en \(\textbf{C}\). Entonces $$\zeta_K(2)=\frac{a}{b} \sqrt{|d|}\pi^{2r_1+2r_2}\text{det}\bigl(D(\sigma_i(\xi_j))\bigr).$$ (dónde \(a/b\) es un número racional no especificado).
Zagier expone además conjeturas semejantes para los valores \(\zeta_K(n)\) para cualquier número natural \(n\), cambiando las funciones \(D(z)\) por otras funciones análogas más complicadas y el grupo de Bloch por otros de orden superior.
Todas estas conjeturas tienen la debilidad del número racional \(a/b\) no especificado. Si uno quiere una conjetura completa necesita tener alguna idea de qué son estos números. Ya desde su trabajo en 1986 Zagier añade: No conocemos de ninguna prueba directa, por ejemplo, de la igualdad de los lados derechos en (5) y (6). Que salvo equivalencias fáciles se traduce en que no conoce una demostración directa de \(I=S\).
Este es el problema, queremos probar \(I=S\), sí, pero queremos una prueba analítica, que no use el teorema de Humbert y las profundas ideas geométricas de Thurston. En el caso de \(I=S\), tenemos una prueba, pero una prueba analítica, podría extenderse a los otros casos de igualdades $$\frac{a}{b}\mathop{\rm vol}(\mathcal M)=\frac{(-D)^{3/2}}{(2\pi)^{2n-4}}\frac{\zeta_K(2)}{\zeta(2)},$$ y aportar luz sobre el significado de la fracción \(a/b\).
Este es el problema que Zagier planteaba en 1986 y ese sigue estando en pie.
Don Zagier.
Es director del Max Planck Institute for Mathematics, Tiene notables resultados sobre Aritmética y Formas Modulares. Sus trabajos son siempre hermosos, como ejemplo tenemos la prueba en una línea de que cualquier primo \(p\equiv1\pmod4\) puede escribirse como suma de dos cuadrados:
Zagier, D., A one-sentence proof that every prime \(p\equiv1\pmod4\) is a sum of two squares, American Math. Monthly, 97, (2) (1990), 144.

Para saber más.
El problema fue propuesto en:
Bailey, D. H. , y Borwein, J. M., Experimental Mathematics: Examples, Methods and Implications, Notices Amer. Math. Soc. 52, (2005), 502-514.
Borwein, J. M., y Bailey, D. H., Mathematics by Experiment, A. K. Peters Ltd., Natick, MA, 2004.
También puede encontrarse en el interesante artículo experimental
Borwein, J. M., y Broadhurst D. J., Determination of rational Dedekind-zeta invariants of hyperbolic manifolds and Feynman knots and links, arXiv:hep-th/9811173 (1998).
Las ideas de Thurston están expuestas en su libro:
Thurston, W. P. The Geometry and Topology of Three-Manifolds, Princeton University, Mimeographed Notes, 1977. Revised version in 2002.
Casi todos los trabajos de Zagier pueden descargarse de su página web: El trabajo en Inventiones Mathematicae donde prueba \(I=S\) es:
Zagier, Don, Hyperbolic manifolds and special values of Dedekind zeta-functions, Invent. Math. 83, (1986), 285–301.
Zagier es un gran matemático pero también un gran comunicador. Su presentación de las hermosas propiedades del dilogaritmo es magnifica:
Zagier, Don, The dilogarithm function, Frontiers in number theory, physics, and geometry. II, 3–65, Springer, Berlin, 2007.
Finalmente, citamos su trabajo sobre sus conjeturas:
Zagier, D, y Gangl, H., Classical and elliptic polylogarithms and special values of L-series, The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), 561–615, NATO Sci. Ser. C Math. Phys. Sci., 548, Kluwer Acad. Publ., Dordrecht, 2000.
Una prueba de la parte fácil de la derivación de \(I=S\) a partir de la igualdad probada por Zagier se encuentra en el artículo:
D. Cvijović, Proof of the Borwein-Broadhurst conjecture for a dilogarithmic integral arising in quantum field theory, arXiv 1011.0195 (2010)

Dejar una contestacion