Como han notado algunos lectores, el enunciado del divertimento Arco entero era erróneo. Pedimos disculpas por el fallo en la redacción. Esta vez, en lugar de dar una solución, aportaremos algunos contraejemplos.
Divertimento:
Un arco de circunferencia pasa por tres puntos \(A\), \(B\) y \(C\), de modo que \(B\) es el punto del arco de altura máxima respecto al segmento \(AC\).

Probar que si el radio de la circunferencia y las longitudes de los segmentos \(AC\) y \(BD\) son números enteros, entonces \( AC\) es un número par de veces \(BD\).
Comentario:
Al extender el segmento de radio BD hasta el centro E, definimos un triángulo rectángulo CDE, cuyos lados miden \(b/2\), \(R-h\) y \(R\), respectivamente.
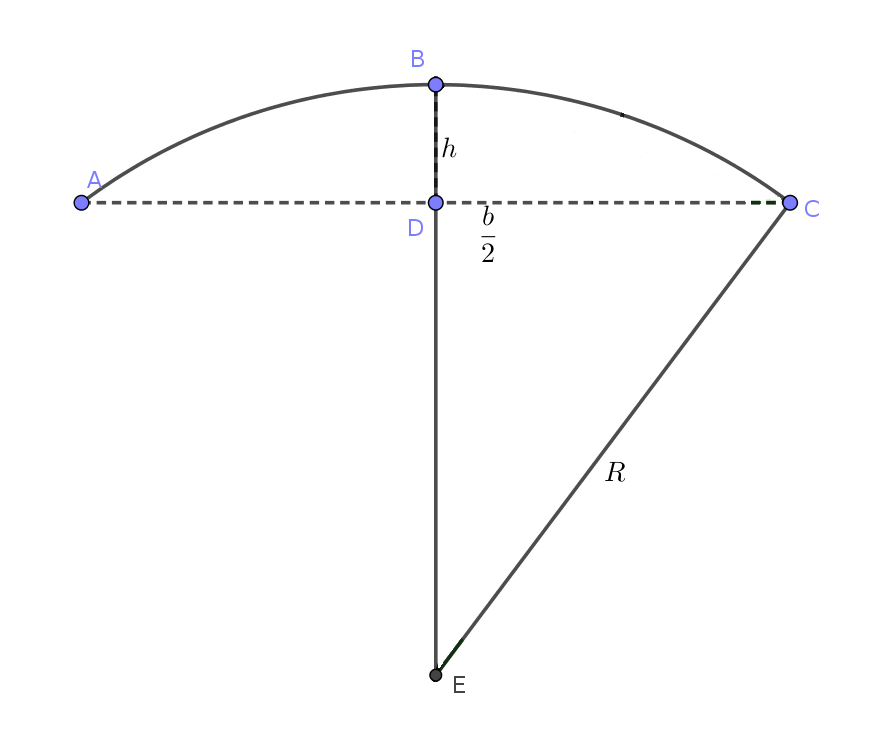
Aplicando el teorema de Pitágoras, obtenemos que \(R^2=b^2/4+(R-h)^2\), que podemos reescribir como
$$2Rh=h^2+\frac{b^2}{4}.$$
Como algunos lectores nos han indicado, es sencillo dar con soluciones enteras a esta ecuación, existiendo incluso familias infinitas. Por ejemplo, para cualquier entero \(k>1\), podemos tomar
$$R=k^2+1,\quad b=2(k^2-1),\quad h=(k-1)^2,$$
datos para los que \(b/h=2(k+1)/(k-1)\). Otra familia viene dada para cualquier entero positivo e impar \(x\), definiendo
$$R=\frac{x^2+1}{2},\quad b=2x,\quad h=x^2,$$
de modo que \(b/h=2/x\). Como se puede comprobar, solo para valores concretos de los parámetros conseguimos que \(b/h=2\).

Muy interesante, es increible la cantidad de aspectos cotidianos de las que las matematicas forman parte.