El problema de Collatz

Collatz (1910–1990) fue un matemático que trabajó principalmente en análisis numérico. Estudió en Alemania entre 1928 y 1935 y como era costumbre cursó en diversas universidades: Munich, Göttingen y Berlin. No nos sorprende que le impresionaran profundamente las clases de Hilbert, Courant, von Mises, Landau y Schur. Fue motivado por las clases de estos dos últimos profesores que trató de representar las funciones aritméticas por grafos. Para ello unía \(n\to m\) cuando \(f(n)=m\). Los ciclos son especialmente interesantes en estos grafos, de manera que trató de definir funciones simples que dieran lugar a ciclos. Para ello debería tenerse números tal que \(f(n)<n\) y otros con \(f(m)>m\). Fue de este modo que definió la función (que hoy llamamos de Collatz) $$C(n)=\begin{cases} n/2 & \text{si $n$ es par},\\ 3n+1 & \text{si $n$ es impar}.\end{cases}$$ Jugando con ella, se encuentra que cualquier número termina en el mismo ciclo \(4\to2\to1\to4\) $$26\to13\to 40\to20\to10\to5\to16\to8\to4\to2\to1$$ Esto llevó a Collatz a formular su conjetura: 

Conjetura:  Aplicando reiteradamente la función de Collatz \(C\) a un número cualquiera llegaremos al número \(1\). 

Para Collatz esto no fue nunca más que un entretenimiento. No publicó nada sobre la función hasta mucho más tarde y únicamente lo comunicó a algunos matemáticos en su entorno. En el congreso internacional celebrado en Cambridge, Mass., en 1950 lo planteó a diversos participantes y el problema se difundió notablemente.

Ciertamente es un problema peligroso, Erdös (que no fue un pusilánime respecto a problemas matemáticos) dijo de este: Hopeless, Absolutely hopeless. El problema apareció publicado por primera vez en un artículo del gran geómetra Coxeter:

Estoy tentado de seguir el ejemplo de Paul Erdös, que ofrece premios al que resuelva ciertos problemas. Si la anterior conjetura es cierta, daré un premio de 50 dólares a la primera persona que me envíe una demostración que yo pueda entender. Si es falsa, ofrezco un premio de 100 dólares al primero que muestre un contraejemplo.

La verdad es que yo no entiendo a Coxeter, ofreciendo premios por problemas que cualquiera puede entender. ¿De verdad pensaba intentar entender cada demostración que le mandaran? 

Algunos argumentos heurísticos.

Tomemos un número impar \(n\), se transforma en \(C(n)=3n+1\) que es par, luego el siguiente número \(C_2(n)=\frac{3n+1}{2}\). Este puede ser par o impar y en general no podemos decir más. Pero ciertamente, terminaremos por llegar a un número \(\frac{3n+1}{2^a}\), siendo \(a\) tal que \(2^a\) divide a \(3n+1\) pero \(\frac{3n+1}{2^a}\) es impar. Denotamos este máximo \(a\) por \(\nu_2(3n+1)\). Podemos de este modo definir la función de Siracusa \(S\) definida sólo en los números impares $$S(n)=\frac{3n+1}{2^{\nu_2(3n+1)}}.$$ Las iteradas \(S_k(n)\) no son más que los números impares entre las iteradas \(C_k(n)\) de la función de Collatz. Así que la conjetura de Collatz equivale a decir que la órbita \((S_k(n))\) contiene a \(1\). 

Si \(n\) es realmente grande, queremos saber qué podemos esperar sobre el tamaño de \(S(n)\). Este puede ser $$\frac{3n+1}{2}, \frac{3n+2}{4}, \frac{3n+2}{8}, \frac{3n+2}{16}, \dots$$ el último que sea entero. Pero un número par al azar es divisible por 2 y no por 4 la mitad de las veces, es divisible por 4 y no por 8 la cuarta parte de las veces, etc. Luego podemos pensar que \(S(n)=\frac{3n+1}{2}\) con probabilidad \(1/2\), \(S(n)=\frac{3n+1}{4}\) con probabilidad \(1/4\), y en general \(S(n)=\frac{3n+1}{2^a}\) con probabilidad \(1/2^a\).

Cuando \(n\) es realmente grande tendremos que \(\log S(n)\) es con mucha aproximación $$\log \frac{3n+1}{2^a}\approx \log\frac{3n}{2^a}.$$ Por tanto el valor esperado de \(\log S(n)\) es 

$$\sum_{a=1}^\infty (\log{3n}-a\log 2)\cdot\frac{1}{2^a}=\log 3n-2\log 2$$ y \(S(n)\) en media será \(\frac{3n}{4}\). Luego esperamos que en promedio los valores de los iterados decrezcan como \((3/4)^k n\), y esperamos que en media llegue a 1 cuando \(\log n=k\log(4/3)\). 

Estos resultados son bastante ajustados a la realidad. Denotemos por \(\sigma(n)\) el menor \(k\) tal que \(S_k(n)=1\). Modelos más complicados predicen que el cociente \(\frac{\sigma(n)}{\log n}\le 41.6776\). Se encuentra experimentalmente que para los valores que se han calculado se tiene $$\frac{\sigma(n)}{\log n}\le 36.7169$$ que se alcanza para \(n=72\,19136\,41637\,72362\,71195\). 

Dificultad del problema.

La conjetura de Collatz tiene un enunciado simple, pero los intentos de probarla han sido infructuosos. Erdös comentó en cierta ocasión: Mathematics is not ready for such problems, y es posible, pero justamente son los problemas difíciles los que son interesantes. Indican algo que no entendemos bien. Un problema fácil, que podemos atacar con nuestras herramientas no nos aportará nuevas teorías y métodos que podamos aplicar posteriormente. 

Es cierto que, como dijo Hilbert, un problema debe ser difícil, pero no tanto que nuestros esfuerzos sean completamente vanos. Pero bueno, hoy hablamos del problema por un avance de hace unos meses sobre este problema. Y el libro de Lagarias sobre la conjetura, publicado en 2010, contiene una bibliografía sobre el tema que contiene 8 artículos publicados en los 60, 34 en los 70, 52 en los 80 y 103 en los 90. Por muy difícil que nos parezca, la conjetura de Collatz tiene muchos puntos por donde atacarla. Esos trabajos conectan el problema con la Teoría de Números, los Sistemas Dinámicos, la Teoría Ergódica, los Procesos Estocásticos y Probabilidades, Teoría de la Computación y Lógica Matemática. De manera que podemos decir que es un problema bien conectado. 

Creo que es un modelo de cómo trabajamos los matemáticos. Ante un problema como este, hacemos todo tipo de experimentos para tratar de encontrar regularidades que nos acerquen a la solución. Por ejemplo, si calculamos el máximo \(\max_C(n)\) número que aparece en la órbita de \(n\) y representamos los puntos \((n,\max_C(n))\) encontramos el gráfico:

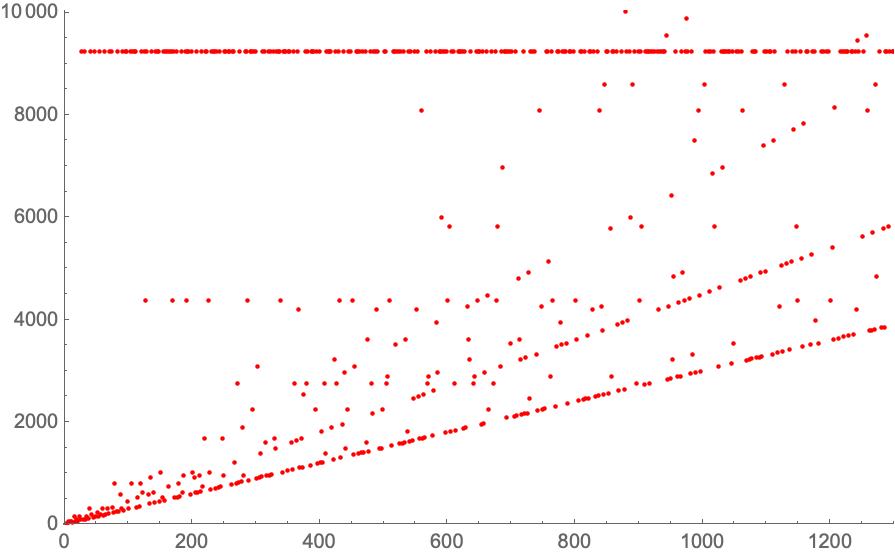
La línea horizontal en la parte superior corresponde a una órbita que contiene muchos números naturales, todos los términos de la órbita comparten el \(\max_C(n)\). Pero, ¿cuál es el motivo de las lineas de pendiente creciente que se dibujan? 

En otras ocasiones los cálculo simplemente nos informen de lo que sucede. Así se ha comprobado que la conjetura de Collatz se cumple para \(n< 10^{20}\).  Otra posibilidad es  generalizar el problema. Problemas muy parecidos en su formulación se comportan de manera muy diferente, por ejemplo si tomamos \(T(n)=n/2\) si \(n\) es par y \(T(n)=(5n+1)/2\) si es impar, entonces casi todas las órbitas escapan a infinito. Se ha reducido el problema de numerosas formas, por ejemplo Monks usando ideas de Conway propone el siguiente equivalente:

Consideremos el conjunto de fracciones \((f_j)\) $$\frac{1}{11}, \frac{136}{15}, \frac{5}{17}, \frac{4}{5}, \frac{26}{21}, \frac{7}{13}, \frac17, \frac{33}{4}, \frac52, 7$$ Para cada \(n\) definimos \(M(n)\) como el primer producto \(nf_j\) que sea un entero. Entonces la conjetura de Collatz es equivalente a que partiendo de \(2^n\) y aplicando sucesivamente \(M\) llegaremos siempre al número \(2\). Por ejemplo $$4\to33\to3\to21\to26\to14\to2.$$

Algunos avances.

Designemos por \(\min_C(n)\) el mínimo de los valores contenidos en la órbita de \(n\). Naturalmente la conjetura equivale a decir que \(\min_C(n)=1\) para todo \(n\), pero estamos tratando de probarla y no vamos a admitir esto. 

Krasikov y Lagarias han probado que hay muchos números que cumplen la conjetura, más precisamente $$\text{cardinal}\{n\le x\colon \min{}_C(n)=1\} \gg x^{0.84}.$$ Ciertamente son muchos, pero es una minoría. Sí, pero es lo que sabemos probar. 

En otro orden de ideas Terras probó que \(\min_C(n)<n\) para casi todo \(n\). Es decir que la órbita desciende por debajo de \(n\). La frase casi todo aquí se refiere a que la proporción de números \(\le x\) que cumple esto tiende a \(1\) para \(x\to\infty\). Este resultado fue mejorado por Allouche y posteriormente por Korec para finalmente llegar a que para casi todo \(n\) se tiene \(\min_C(n)<n^\theta\) siendo \(\theta\) cualquier número \(>\frac{\log3}{\log4}=0.7924\). 

Si hoy hablamos del problema es porque T. Tao el mes pasado ha publicado en arXiv un artículo mejorando estos últimos resultados.

El trabajo de Terry Tao.

Tao resume su teorema en la frase: Casi todas las órbitas alcanzan valores casi acotados.

Teorema. Sea \(f\colon\textbf{N}\to\textbf{R}\) una función tal que \(\lim_{n\to\infty} f(n)=+\infty\), entonces tendremos que para casi todo \(n\) se cumple \(\min_C(n)<f(n)\).

La gracia del teorema de Tao es que podemos escoger una función que tienda a infinito tan lentamente como queramos, por ejemplo \(f(n)=\log\log\log\log n\).

Por el teorema de Korec para casi todo \(n\in[1,x]\) se tiene \(\min_C(n)<x^\theta\), y también para casi todo \(m\in[1,x^\theta]\) se tiene \(\min_C(m)<(x^\theta)^\theta=x^{\theta^2}\). ¿No podríamos tomar \(m=\min_C(n)\), para llegar a la conclusión de que para casi todo \(n\in[1,x]\) se tiene \(\min_C(n)<x^{\theta^2}\)? Al fin y al cabo toda la órbita de \(m=\min_C(n)\) está contenida en la órbita de \(n\). Tao explica que ese razonamiento no es correcto debido a que casi todo no es todo y puede suceder que los \(m=\min_C(n)\) estén todos en el conjunto excepcional. 

En cualquier caso toda la prueba de Tao (el artículo tiene 48 páginas) se basa en hacer riguroso este razonamiento y llevarlo a su límite, es decir que en lugar de \(x^a\) aparece una función arbitraria con la única condición de que tienda a infinito.

La afirmación de que casi todas las órbitas toman valores casi acotados, se refiere a valores menores que \(f(n)\). La función \(f\) no es acotada, tiende a infinito, pero es lo más próximo que podemos imaginar a acotada. 

Tao usa la frase para casi todo \(n\) en un sentido especial, se refiere a la densidad logarítmica \(0\). Un conjunto \(A\) de números naturales tiene densidad logarítmica \(\alpha\) si se cumple $$\lim_{x\to\infty}\frac{\sum_{n\in A, n\le x}\frac1n}{\sum_{n\le x}\frac1n}=\alpha.$$ Esta densidad tiene propiedades que la hacen indispensable en la prueba, manteniendo el sentido intuitivo de para casi todos los \(n\). Otro elemento fundamental es usar la función de Siracusa. Se prueba fácilmente que el teorema es equivalente al enunciado \(\min_S(n)=1\) en lugar de \(\min_C(n)=1\). 

Cuando aplicamos la función de Siracusa a \(n\), \(S(n)=(3n+1)/2^{\nu_2(3n+1)}\). La valuación \(\nu_2(3n+1)\) tiene aquí un valor importante. Necesitamos también controlar cómo varían las valuaciones de las sucesivas iteradas. De manera que Tao define la función $$a^{\to}_{(k)}(n)=\bigl(\nu_2(3n+1), \nu_2(3S(n)+1), \dots, \nu_2(3S^{k-1}(n)+1)\bigr).$$ Un principio heurístico que le conduce en la prueba es el siguiente:

Principio Heurístico: Si \(n\) es un natural típico grande impar y \(k\) es mucho menor que \(\log n\), entonces la valuación \(a^{\to}_{(k)}(n)\) se comporta como un conjunto de \(k\) variables aleatorias independientes distribuidas según la ley \(\mathbb{P}(X=a)=2^{-a}\). 

Este principio está de acuerdo con los argumentos heurísticos explicados anteriormente. Naturalmente la parte difícil del trabajo es convertir estas ideas vagas en desigualdades matemáticamente correctas. 

Una vez conseguido eso, Tao usa otra comparación que lo guía en su razonamiento. Esta vez afirma que lo conseguido le recuerda en el lenguaje de las ecuaciones diferenciales, cuando se tiene un buen control de la evolución a corto plazo (\(k\ll\log n\)), para casi todas las elecciones de las condiciones iniciales (\(n\)). Esto situación en EDP se denomina en inglés almost sure local wellposedness. Para pasar a almost sure almost global wellposedness se inspira en un trabajo de Bourgain,  donde Bourgain construyó una medida de probabilidad invariante. Para la situación análoga en el problema de Collatz no existe esa medida y tiene que recurrir a construir una familia de medidas que aproximadamente se transforman unas en otras mediante la función de Siracusa.

Es lo que siempre me sorprende de Tao, como es capaz de usar técnicas desarrolladas en un campo de las Matemáticas a otros completamente dispares. Pero eso es lo que hacemos los matemáticos aplicar a nuestros problemas técnicas desarrolladas para resolver otros problemas. Sólo que Tao tiene una habilidad especial.

Para saber más.

La mejor fuente de información sobre el problema de Collatz es el libro de Lagarias:

Jeffrey C. Lagarias, The Ultimate Challenge: The $3x+1$ Problem, Amer. Math. Soc., Providence, Rhode Island, 2010.

En particular resultados sobre la posibilidad de que la conjetura sea indecidible, de los que no hemos indicado nada. 

El trabajo de Tao que comentamos puede bajarse de arXiv:

T. Tao, Almost all orbits of the Collatz map attain almost bounded values, arxiv:1909.03562.

En internet se encuentran numerosas referencias al problema:

Numberphile:David Eisenbud sobre la Conjetura de Collatz