A veces las Matemáticas se comparan con el Ajedrez y es cierto que tienen mucho en común. Pero hay una diferencia muy importante. En el Ajedrez lo que más cuenta es la peor jugada, en cambio en Matemáticas lo que cuenta es la mejor jugada. Seguro que Marithania, la protagonista de nuestra historia hoy lo puede ratificar. ¿Cuántos ensayos no habrá hecho antes de dar con el nudo \(10_{145}\) que destruía la conjetura de Kauffman? En el Ajedrez una mala jugada hace perder la partida, no importa cuán buenas fueran todas las demás jugadas. En cambio los intentos infructuosos de demostrar un resultado matemático no cuentan para el éxito final.

Las tablas de Dale Rolfsen
Marithania trabaja con nudos un concepto matemático, pero muy intuitivo. Si cogemos una cuerda, la atamos y pegamos los extremos, lo que obtenemos es un nudo. Los matemáticos empezaron a interesarse por ellos sobre todo al final del siglo XIX, pero ya Gauss los consideró un poco antes.
El libro de Dale Rolfsen Knots and Links tiene 439 páginas. Desde la página 321 a la 429 contiene las figuras y notaciones de unos 1000 nudos y (links) o enlaces de nudos, como los anillos de Borromeo de los que hablé en otra entrada. Cada página contiene unos 10 nudos, de los que la figura muestra el ejemplo que usó Marithania. Es en esa maraña donde ella ha buscado su nudo preferido. Con ello ha resuelto una conjetura planteada por Louis H. Kauffman en 1983.
Las tablas de nudos tienen una historia larga. En 1877 P. G. Tait comenzó el trabajo de la enumeración de los nudos. Lord Kelvin, mirando los anillos de humo de algunos fumadores, pensó que los átomos estaban formados por un flujo de partículas en movimiento que describían una trayectoria cerrada. La distinta naturaleza de los elementos químicos se debía al nudo descrito por esa trayectoria. Quizás hoy los físicos están volviendo a esa idea cuando hablan de la teoría de cuerdas en que las partículas fundamentales se reemplazan por objetos unidimensionales.
En todo caso el problema fundamental es decidir si dos nudos son equivalentes. Entendiendo por equivalentes que exista un homeomorfismo del espacio que lleve una al otro. O mejor, que sin romperlos, pero quizás estirando o comprimiendo trozos de la cuerda, podemos transformar un nudo en el otro.
Las tablas de Rolfsen se publicaron por primera vez en 1976, se han reeditado, la última vez en 2003, pero sin modificaciones sustanciales. Por eso todavía podemos ver el par de Perko. Rolfsen añade en la última edición la nota: One of the most embarrassing errors is the duplication in the knot table: \(10_{161}\) and \(10_{162}\) are really te same knot, as K. Perko has pointed out.
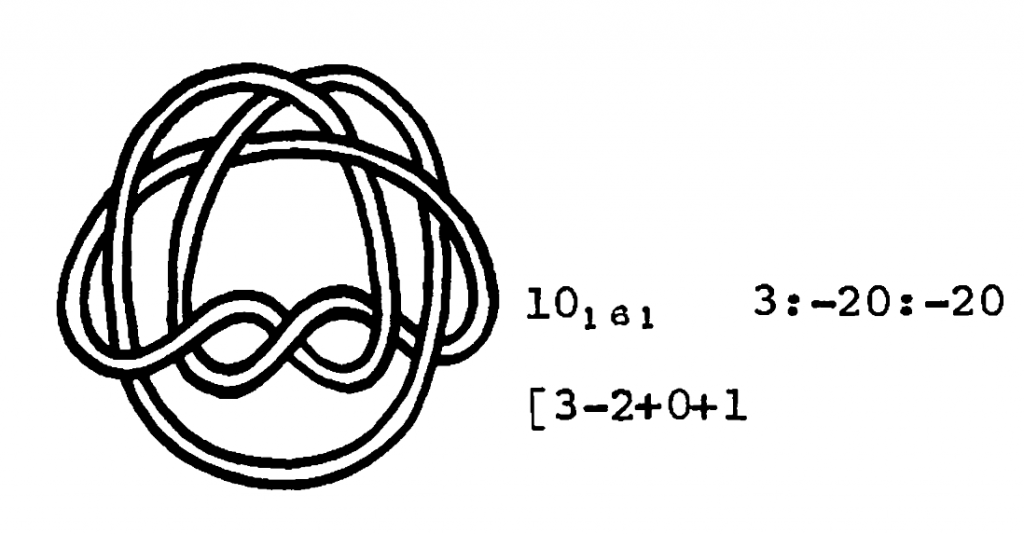

Aquí vemos la dificultad de distinguir los nudos. Estos dos aparentemente distintos son en realidad el mismo presentado de dos maneras distintas. De Perko estuve a punto de hablar en la entrada que dediqué a los matemáticos amateurs. Perko trabajaba como abogado y solo en sus ratos libres se dedicaba a los nudos. Pero sin embargo sí que tenía estudios en Ciencias de la Computación. La teoría de nudos está muy desarrollada y se han descubierto numerosos métodos de ver que dos nudos no son iguales. En realidad un nudo se puede representar por un diagrama, que no es más que una proyección del nudo, en la que los puntos dobles han sido sustituidos por cruces en los que se indica qué trozo de la cuerda pasa por arriba y cuál por abajo
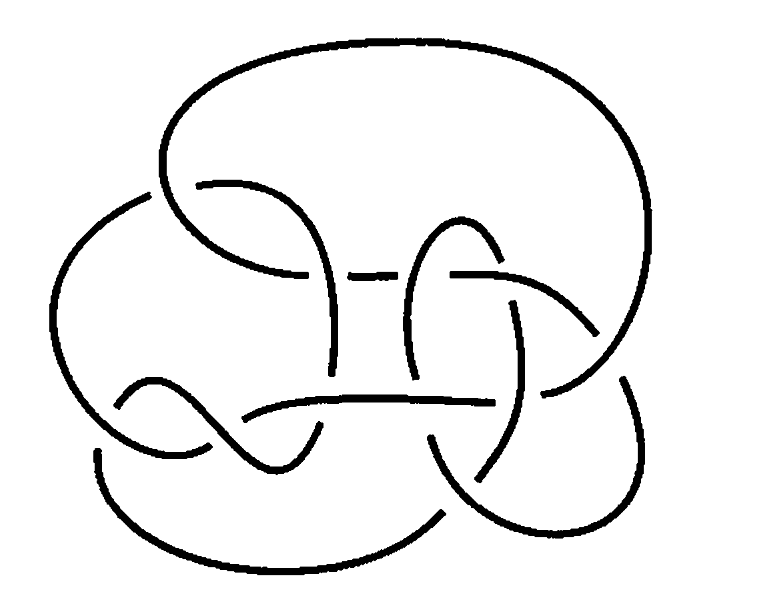
Y dos diagramas representan el mismo nudo si y sólo si pueden transformarse uno en otro mediante los movimientos de Reidemeister
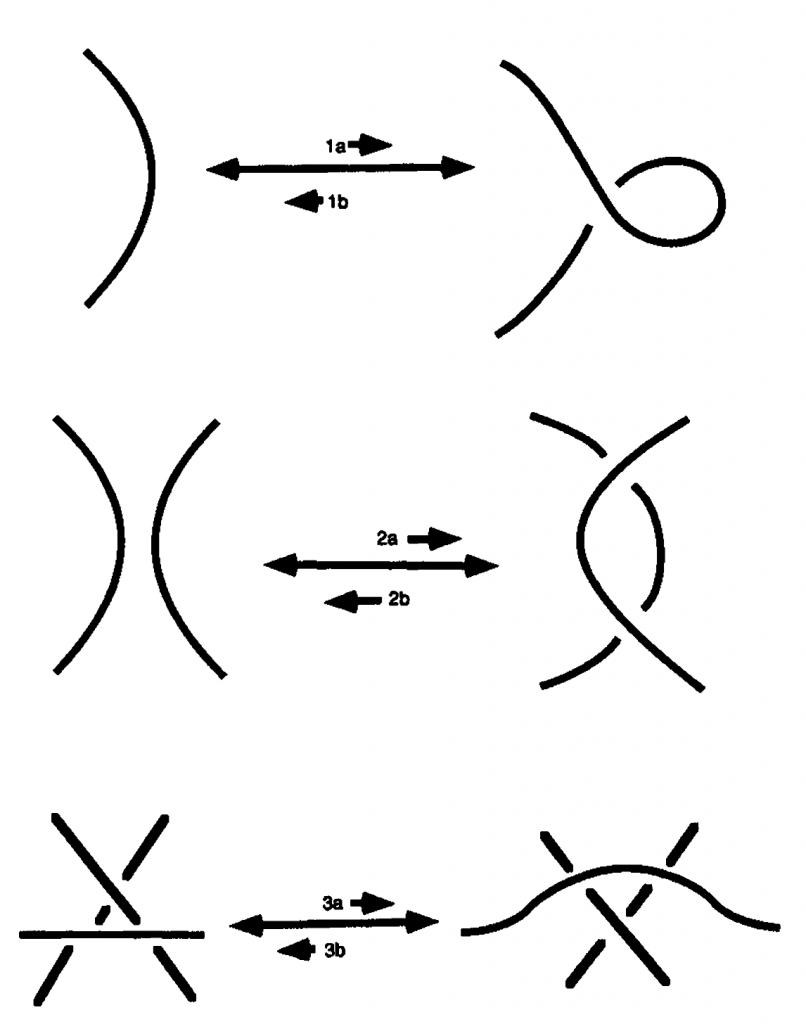
Nudos alternativos.
Hay muchas cosas interesantes que contar sobre los nudos, pero trataremos de explicar justo lo necesario para entender cuál es el problema que ha resuelto Marithania. Empezaremos por decir que se han definido numerosas clases de nudos. Por ejemplo, un nudo es alternante si puede representarse mediante un diagrama que al ser recorrido haga que pasemos, alternativamente, por arriba y por debajo cada vez que encontremos un cruce.
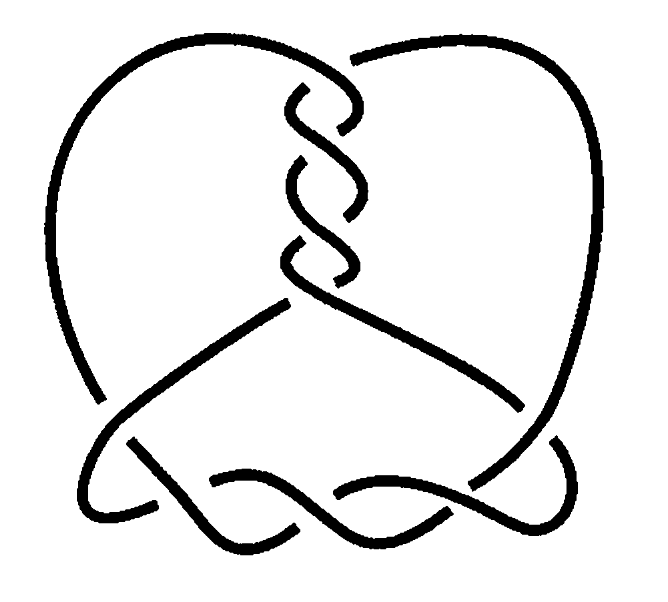
Kauffman en 1983 definió una clase relacionada la de los nudos alternativos. Para ello se definen los diagramas alternativos. Un nudo será alternativo si admite una representación por un diagrama alternativo.
Para poder hablar de un diagrama alternativo tenemos que partir de un diagrama orientado, es decir, un diagrama de un nudo en el que hemos fijado una de las dos orientaciones posibles. Los cruces de un diagrama orientado se pueden clasificar en positivos y negativos. Lo hacemos de acuerdo con el diagrama en la figura:

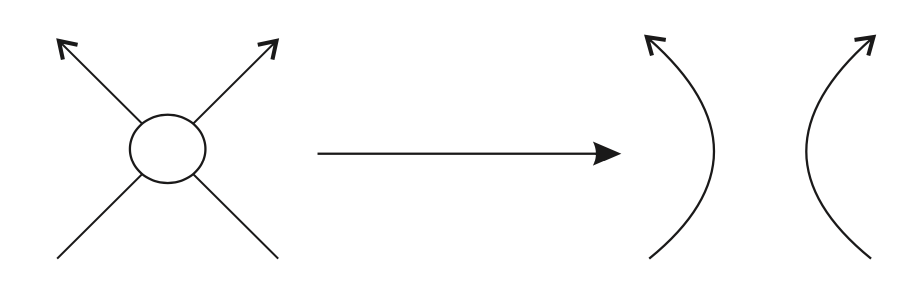
A continuación eliminamos los cruces mediante el procedimiento indicado, obteniendo una serie de círculos, posiblemente anidados, en el plano. Estos círculos dividen el plano en distintas componentes conexas. Diremos que el diagrama de partida es alternativo si en cada componente conexa todos los cruces tienen igual signo. Como dijimos antes, un nudo es alternativo si existe un diagrama alternativo que lo represente. Por ejemplo veamos que el diagrama que vimos antes no es alternativo
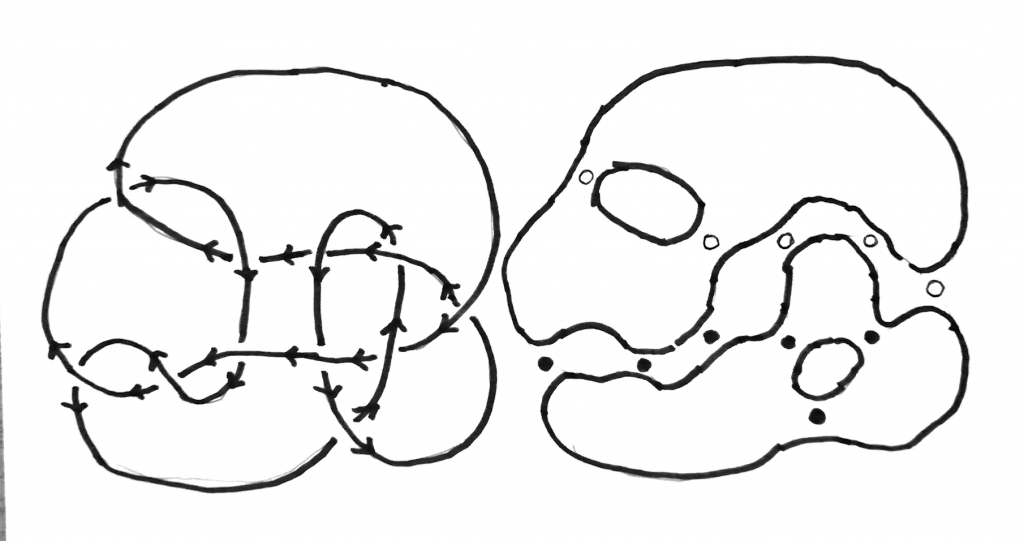
En la primera figura hemos preparado para saber cuales cruces son positivos o negativos. En la segunda figura hemos eliminado los cruces y hemos puesto un punto negro en los positivos y una pequeña circunferencia en los negativos. Vemos que la componente no acotada contiene 3 cruces positivos y 3 negativos, luego el diagrama no es alternativo. Esto no quiere decir que el nudo del diagrama no sea alternativo, pudiera existir otro diagrama para el mismo nudo que sí sea alternativo. Esta dificultad es una de las que ha tenido que salvar Marithania para demostrar que su nudo \(10_{145}\) no es alternativo.
Nudos seudoalternantes.
La conjetura de Kauffman se refiere también a otra clase de nudos. El Teorema de Seifert asegura que todo nudo puede verse como el borde de una superficie orientable
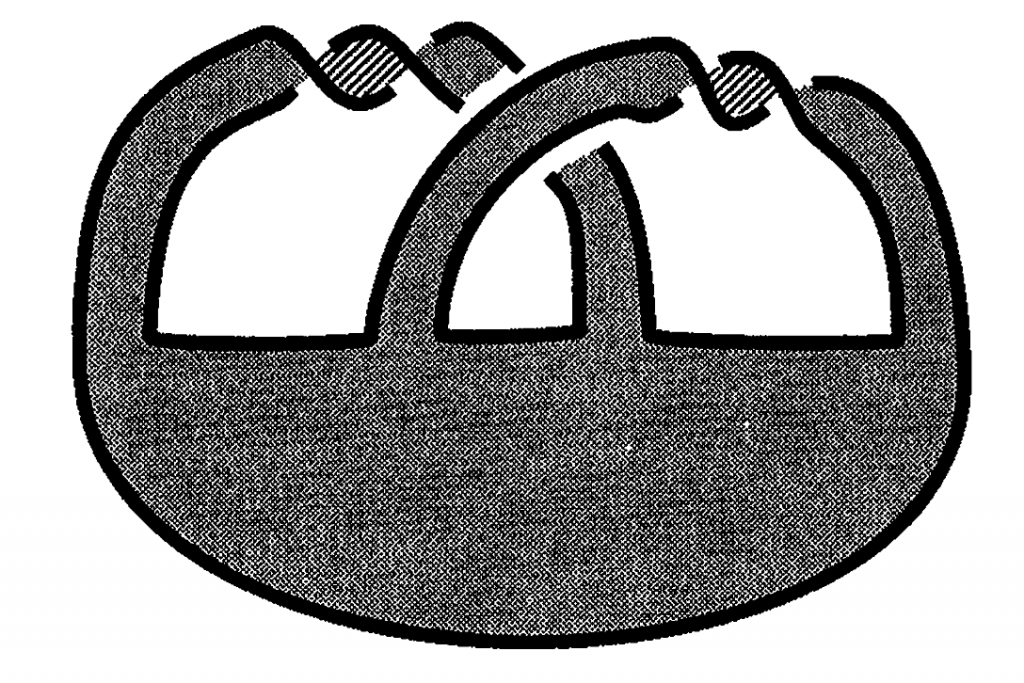
Los nudos seudoalternantes serán aquellos que sean el borde de una superficie plana generalizada. Superficies planas primitivas son las formadas por varios discos unidos por bandas con un solo twist todos en la misma dirección, estas bandas son todas disjuntas dos a dos y pueden dibujarse en un plano. Una superficie plana generalizada es la que se obtiene identificando discos de superficies planas primitivas:
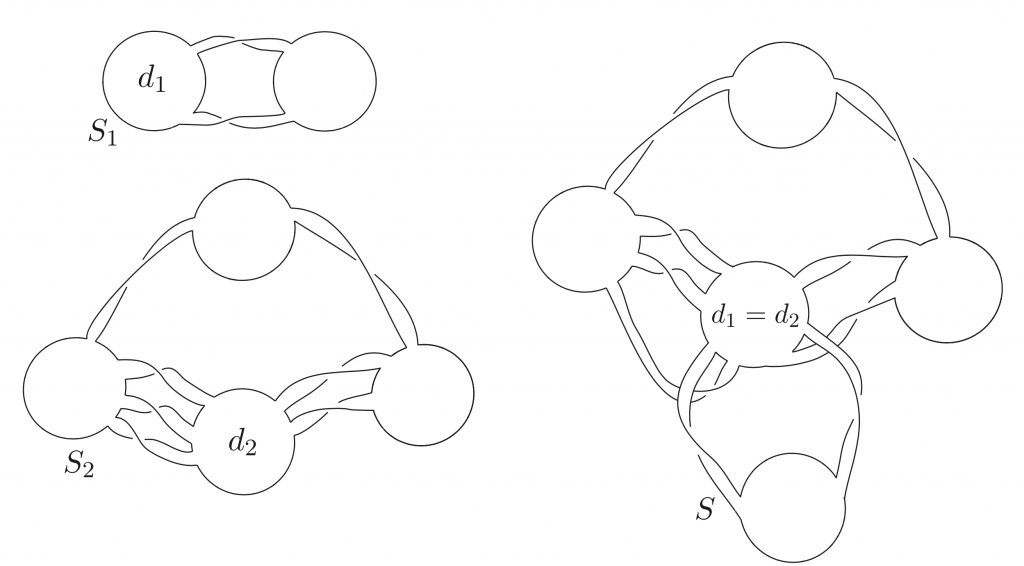
\(S_1\) y \(S_2\) son superficies planas primitivas. Identificando los discos \(d_1\) y \(d_2\) se obtiene la superficie plana generalizada \(S\).
La conjetura de Kauffman.
Los nudos seudoalternantes habían sido definidos por E. J. Mayland y K. Murasugi en 1976 como una generalización de los nudos alternantes. Kauffman en 1983 define los nudos alternativos. Kauffman probó en su trabajo que los nudos alternativos son seudoalternantes y planteó la cuestión de si las dos clases son iguales. Aún cuando los nudos alternativos no estaban definidos, en cierto sentido Mayland y Murasugi también plantearon la cuestión. Marithania Silvero prueba que el nudo \(10_{145}\) es seudoalternante pero no alternativo. Demostrar que el nudo \(10_{145}\) es seudoalternante requiere ponerlo como borde de una superficie plana generalizada. Esto lo hace mediante unos movimientos de Reidemeister que llevan \(D_1\) en \(D_4\) y mostrando la superficie.
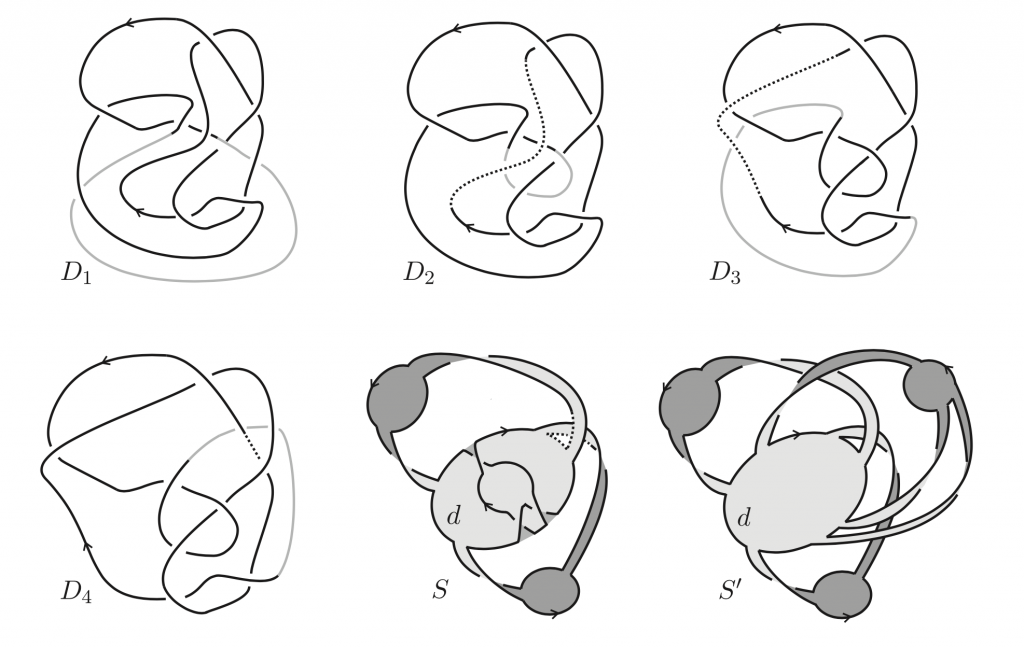
Pero la prueba de que no es alternativo no puede ser tan directa. Habría que considerar todas los diagramas posibles de \(10_{145}\). Se usa una clase intermedia la de los grafos homogéneos, introducidos por Peter Cromwell en 1989 y una buena porción de Teoría de nudos para dar una prueba elegante. El que quiera enterarse de la prueba necesitará estudiar algo de teoría de nudos para entender el trabajo de Marithania.
Sobre la investigación matemática.
Marithania dio una conferencia sobre su resultado en la Facultad. Nos contó que a ratos trataba de probar la conjetura y a ratos intentaba buscar un contraejemplo. No lo hemos dicho, pero en las dos direcciones consiguió resultados: su tesis contiene la prueba de que la conjetura es cierta para links cuyo primer número de Betti sea \(\le 2\).
Hemos explicado algo del significado de los nudos alternativos y los seudoalternantes, pero a los que no somos expertos en nudos nos pueden parecer definiciones caprichosas. Pero esto no es así, cuando Kauffman los define es porque los necesita con un objetivo preciso. Son conceptos naturales dentro de la teoría. Marithania estará siempre asociada a la relación entre estos dos tipos de nudos. Es lo que tiene la Matemática, las palabras de un poema o su significado habrán cambiado en 1000 años pero la belleza matemática es atemporal. Es más duradera que la de cualquier otro arte.
Las palabras de Marithania en la conferencia me recordaron algunas de mis experiencias y al escribir esto pensé que era bueno que ampliara lo que contó. Su respuesta es muy interesante para entender el proceso de la investigación matemática y de paso sirve para destruir el mito de los descubrimientos por serendipia. Suerte de la que algunos hablan para justificar su inactividad. Creo que no puedo mejorar su propia descripción:
Yo estaba intentando probar la conjetura al tiempo que intentaba refutarla. En el proceso de intentar probarla, iba descartando situaciones para las que tenía una prueba, y preguntándome «¿qué podría hacer que la prueba para este caso fallara?» Así fui dando con una serie de «situaciones desfavorables» para las que las pruebas que había ido consiguiendo fallaban. La idea era, entonces, partir de un nudo pseudoalternante con algunas de esas «situaciones desfavorables», y construir una prueba que asegurara que el nudo era alternativo. Pero en uno de los ejemplos que construí no sólo no fui capaz de probar que era alternativo, sino que pude asegurar, recurriendo a un invariante de nudos (el polinomio de Conway), que el nudo no podía ser alternativo. En otras palabras: había construido un nudo pseudoalternante que no era alternativo, es decir, un contraejemplo a la conjetura de Kauffman.
En aquel momento, el diagrama del nudo era mucho más complejo que el que se presenta en el artículo: lo que tenía delante era un nudo pseudoalternante escrito como borde de una superficie trenzada con más de 17 cruces. Utilizando invariantes de enlace, pude determinar que en realidad el número de cruces podía ser reducido a 10, y que se trataba, en efecto, del nudo \(10_{145}\).
A partir de su trabajo ha viajado mucho encontrándose en especial con el propio Kauffman. Louis Kauffman es profesor en la Universidad de Illinois en Chicago donde ella ha hecho una estancia después de refutar su conjetura.

Es todo un éxito para nuestra Facultad que Marithania Silvero sea nuestra alumna. Más que su resultado resolviendo un problema de más de 30 años sea parte de su tesis doctoral defendida en el IMUS. Nos llena de orgullo, enhorabuena también a sus directores Juan González Meneses y Pedro González Manchón que la pusieron delante del problema.
Parafraseando a Kronecker y recordando un pasaje de la Odisea: La matemática es como la flor del loto, habiendo probado este alimento los matemáticos no lo pueden dejar. Seguro que Marithania seguirá resolviendo problemas en el futuro.
Para saber más.
La teoría de nudos es uno de los temas que se puede apreciar sin grandes preparaciones previas. Un buen sitio donde empezar puede ser el libro del que hemos usado algunas imágenes en esta entrada:
Charles Livingston, Knot Theory, Mathematical Association of America, Washington, 1993.
El artículo de Marithania es accesible en la red: Marithania Silvero, On a conjecture by Kauffman on alternative and pseudoalternating links, Topology and its appl. 188 (2015), 82-90.
Pero con más amplitud se puede ver su tesis: Marithania Silvero, On some families of links and new approaches to link homologies, Imus 2016.

So who was the better pool player?