Fractales en la poesía

El matemático alemán Felix Hausdorff (1868-1942) enriqueció notablemente en 1919 el concepto de dimensión espacial. Decía Hausdorff que era muy poco sofisticado, e incluso incorrecto, decir que un objeto tiene dimensión uno si sólo tiene longitud ―un hilo, o un muelle, por ejemplo―; dimensión dos si además de longitud tiene anchura ―una hoja de papel o la superficie de una esfera―; y dimensión tres si además de longitud y anchura tiene también altura ―una esfera o una caja de zapatos―. Para enriquecer el concepto clásico de dimensión, Hausdorff propuso una noción mucho más sofisticada y rica desde el punto de vista matemático. La noción de Hausdorff permite medir de manera mucho más precisa la dimensión de un objeto; resulta así que, contra lo que nuestra intuición sensorial nos dice, hay objetos con dimensiones fraccionarias, digamos con dimensiones 1/2 o 5/3, o incluso \(\sqrt 5\), o todavía números peores.

Más de medio siglo después de que Hausdorff precisara su nuevo concepto de dimensión, Benoît Mandelbrot (1924-2010), un matemático de origen polaco aunque criado en Francia, bautizó con el nombre de «fractales» a esos conjuntos cuya dimensión de Hausdorff es fraccionaria. Por así decir, un fractal es un conjunto anómalo para nuestros sentidos, pero esa anomalía tiene que ver con la manera en que estos perciben las dimensiones espaciales; la rareza de un fractal es, por tanto, sensorial y no matemática.

Un ejemplo bien conocido de fractal es la curva de Koch, llamada así en honor del matemático sueco Niels von Koch que la definió en 1906. Hay distintas variantes, aquí voy a construir la curva de Koch partiendo de un triángulo equilátero; para ello se divide cada uno de sus lados en tres partes iguales y se reemplaza el segmento central en cada lado por los dos lados del triángulo equilátero construido sobre dicho segmento central. Se obtiene así una estrella de seis puntas. Se repite otra vez el proceso, o sea, se divide cada uno de los doce lados de la estrella en tres partes iguales y se reemplaza el segmento central en cada lado por los dos lados del triángulo equilátero construido sobre dicho segmento central. La curva de Koch es lo que se obtiene al repetir el proceso infinitas veces. No es difícil calcular que la dimensión de Hausdorff de la curva de Koch vale \(\log 4/\log 3\).

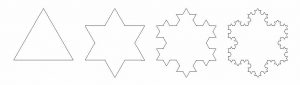
Mandelbrot mostró que la geometría de los fractales suele ser espectacularmente compleja ―no es raro que estén asociados con procesos caóticos―, aunque a menudo esa complejidad surge paradójicamente de una sencilla similitud ―a cualquier escala― entre sus partes.

Los fractales son conjuntos raros, fascinantes y muy laberínticos, y «aparentemente» bastante ajenos a nuestra experiencia física. Y he entrecomillado «aparentemente» porque, en realidad, esos objetos son tan omnipresentes, se colocan delante de nuestros ojos con tanta frecuencia y descaro, tanto nos hemos acostumbrado a su rareza, que ni siquiera somos ya capaces de reconocerla. La geometría fractal abunda más en la naturaleza que la geometría suave de las superficies matemáticas más convencionales. Y un buen ejemplo es que no hay mejor descripción para un litoral carcomido de rías o fiordos, como el gallego o el noruego, que una curva fractal del tipo de la curva de Koch. E, igualmente, nada describe mejor la red de neuronas de nuestro complicado cerebro que un fractal.

Ha sido la mirada matemática ―la aguda visión de matemáticos como Hausdorff o Mandelbrot― la que nos ha permitido reconocer la ubicuidad de los fractales en la naturaleza.

La mirada del matemático pero también la mirada del poeta. De los incontables ejemplos con que podría ilustrarse la coincidencia que se da en este caso entre la visión poética y matemática de la realidad, he elegido dos poemas: una rima de Bécquer y unos versos de Neruda.

Para describir la vaporosa esencia de la inspiración poética, «perfume misterioso de que es vaso el poeta», Bécquer echó mano en una célebre rima de objetos cuya naturaleza sutil y etérea contrasta con la solidez de su constitución tridimensional:

«Yo soy nieve en las cumbres,

soy fuego en las arenas,

azul onda en los mares

y espuma en las riberas.»

La mirada del poeta ha reunido en estos cuatro versos otros tantos objetos equívocamente tridimensionales: pensemos en la vacuidad de la nieve recién caída, el inaprensible hálito de una llama, la transparencia del «azul onda» del mar que lo convierte en un color incorpóreo, inasible por el ojo, un color caótico que no es uno sino muchos, o la porosa hechura de un jirón de espuma.

Consideremos ahora los primeros versos del poema 18 de Veinte poemas de amor y una canción desesperada de Pablo Neruda. Para envolver la irrealidad del amor ejercido en la distancia, «Amo lo que no tengo. Estás tú tan distante», Neruda echó mano en ese poema de objetos de clara naturaleza fractal:

«Aquí te amo.

En los oscuros pinos se desenreda el viento.

Fosforece la luna sobre las aguas errantes.

Andan días iguales persiguiéndose.

Se desciñe la niebla en danzantes figuras.

Una gaviota de plata se descuelga del ocaso.

A veces una vela. Altas, altas las estrellas.»

Pensemos en el tupido entramado de las agujas de los pinos, donde se desenreda el viento, en la porosa espuma que culmina esas aguas errantes sobre las que fosforece la luna, o el inaprensible hálito de un girón danzante de niebla. A lo que hay que añadir la ubicuidad de las altas estrellas, esos puntos que se arraciman en el cielo conformando un mosaico de luz cuya complejidad inasible por el ojo casi alcanza la bidimensionalidad.

Todas esas ambigüedades son, en realidad, consecuencia de la naturaleza fractal de dichos objetos. Ocurre que nuestra pobre percepción visual es incapaz de apreciar la realidad de su dimensión fraccionaria; realidad que, en cambio, se pone de manifiesto al aplicar el afilado bisturí de la dimensión de Hausdorff o la aguda intuición onírica de Bécquer o Neruda.

Referencias:

Antonio J. Durán, Pasiones, piojos, dioses… y matemáticas, Destino, Barcelona, 2009.

Antonio J. Durán, La poesía de los números, RBA, Barcelona, 2011.