Delantal:
El divertimento que nos ocupa esta quincena es un ejemplo simplificado de camino aleatorio en el retículo \(\mathbb{Z}^2\). Estos procesos, englobados a su vez en los de Markov, tienen numerosísimas aplicaciones en todas las ramas de la ciencia y la ingeniería, en donde modelizan (o ayudan a modelizar) fenómenos como la evolución de los precios, la deriva genética, el movimiento de los animales, las sugerencias en redes sociales y muchos más. Incluso da ideas a artistas con ganas de experimentar, como a Antony Gormley a la hora de crear su escultura Quantum Cloud (que ilustra esta entrada).
Si consideramos el límite de estos paseos cuando la longitud de los pasos tiende a cero, estaremos trabajando realmente con un proceso de Wiener, que modeliza el movimiento browniano, que es como se denomina al movimiento aleatorio que sigue una partícula en un medio fluido a raíz de los choques con las moléculas de dicho fluido. Los lectores habituales de este blog habrán oído hablar de él, pues fue Einstein quien dio por primera vez una explicación teórica del fenómeno (corroborada empíricamente años más tarde), publicada en uno de los artículos de su annus mirabilis y que sirvió como argumento a favor de la teoría atómica de la materia.
Divertimento:
Ana y Bernabé quedan para dar una vuelta por la barriada cuyo plano podemos ver en la imagen, en donde se encuentran sus respectivas viviendas. Ambos son un tanto despistados y han salido de casa sin móvil y sin saber en qué sitio quedaban, así que cada uno se dirige a la del otro. ¿Qué probabilidad hay de que se encuentren?
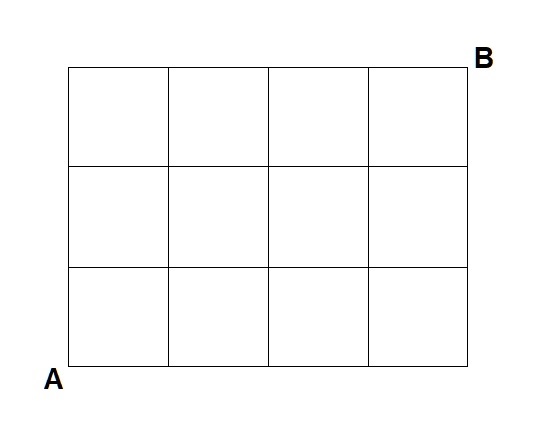
(Nota: Suponemos que ambos inician su camino a la vez, moviéndose a igual velocidad constante, que no dan rodeos y que en cada cruce las dos posibles direcciones son equiprobables.)
Solución:
Envía tus soluciones, hasta el domingo 16 de febrero, a la dirección ‘divertimentos-blog-imus(arroba)us.es’. La solución aparecerá el miércoles 19 de febrero. Recuerda no dejar pistas en los comentarios hasta que no se publique la solución del problema.

No entiendo bien cómo tomarme la definición de no dar rodeos
Queremos decir que se dirigirán hacia el lugar de origen de la otra persona por un camino lo más corto posible.
Alguien podría pensar que cada persona elige su camino de forma determinista, entre todos los caminos posibles de un punto al otro, antes de comenzar el trayecto. Debo entender que la probabilidad es distinta de si se elige una dirección en cada cruce, y sería otro problema, ¿es así?
Entiendo que no; los caminos no son equiprobables, porque su probabilidad depende de la cantidad de cruces por los que pasa cada uno (como se puede ver en la solución).