Publicamos la solución al divertimento de la pareja despistada. Gracias a Jaime Benabent, Gustavo Roque Collado, Magdalena Jáñez, Antonio Navas, Miguel Pineda y Enrique Zubiría por las soluciones que nos han enviado.
Divertimento:
Ana y Bernabé quedan para dar una vuelta por la barriada cuyo plano podemos ver en la imagen, en donde se encuentran sus respectivas viviendas. Ambos son un tanto despistados y han salido de casa sin móvil y sin saber en qué sitio quedaban, así que cada uno se dirige a la del otro. ¿Qué probabilidad hay de que se encuentren?
(Nota: Suponemos que ambos inician su camino a la vez, moviéndose a igual velocidad constante, que no dan rodeos y que en cada cruce las dos posibles direcciones son equiprobables.)
Solución:
Definamos un sistema de coordenadas con origen en \(A\) y unidad el lado de un cuadrado. Como Ana y Bernabé recorren caminos de longitud mínima, Ana solo puede ir arriba o a la derecha y Bernabé a la izquierda o abajo. Todos los caminos tienen longitud siete, así que nuestros protagonistas se encontrarán entre el tercer y el cuarto movimiento. En la figura se marcan con puntos blancos y negros las posibles posiciones de Ana y Bernabé, respectivamente, tras el tercer movimiento de cada uno.
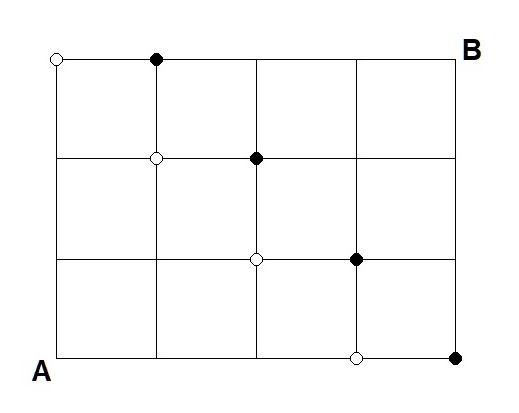
Por la simetría (central) del problema, nos basta probar la probabilidad de que Ana llegue a los distintos segmentos marcados por puntos blancos y negros. Como el movimiento de ambos es independiente del del otro amigo, la probabilidad de que ambos se encuentren en cada segmento será el producto de aquellas con las que cada uno llega a él.
Supongamos que Ana llega a \((0,3)\). Como solo hay un posible camino para llegar allí, lo habrá hecho con probabilidad \(\frac{1}{8}\). Ahora Ana no puede pasar sino a \((1,3)\), con lo que la probabilidad de llegar al segmento entre \((0,3)\) y \((1,3)\) será \(\frac{1}{8}\) también.
Supongamos ahora que Ana llega a \((1,2)\). Tiene tres maneras de llegar a dicho punto, así que la probabilidad de que haya llegado hasta ahí es \(\frac{3}{8}\). Por tanto, la probabilidad de pasar por los dos segmentos que empiezan en dicho punto es \(\frac{3}{16}\). Si Ana llega a \((2,1)\) el resultado es el mismo.
Por último, si Ana llega a \((3,0)\) lo hará con probabilidad \(\frac{1}{8}\), así que alcanzará los dos últimos segmentos con probabilidad \(\frac{1}{16}\).
En conclusión, la probabilidad pedida es así
$$\frac{1}{8}\frac{1}{16}+ \frac{3}{16}\frac{1}{16}+ \frac{3}{16}\frac{3}{16}+ \frac{3}{16}\frac{3}{16}+ \frac{3}{16}\frac{3}{16}+ \frac{1}{16}\frac{3}{16}+ \frac{1}{16}\frac{1}{8}= \frac{37}{256}.$$

Dejar una contestacion