En matemáticas, modelizar es intentar extraer los aspectos significativamente importantes de una situación real y plasmarlos en forma de expresiones y ecuaciones matemáticas. Salvo en procesos muy sencillos, lo que se obtenga nunca va a ser exacto, porque el modelo, necesariamente, no puede captar toda la realidad ni todas las variables involucradas, ni incorporar todos los datos iniciales de los que se parte. Pero sí que puede servir para estudiar el proceso y prever, de alguna forma, cómo la introducción de medidas concretas puede hacer que su evolución futura varíe.
En particular, es lo que ocurre con el desarrollo de las epidemias, y es lo que vamos a intentar hacer aquí mediante el modelo epidemiológico SEIR, bien adaptado a la epidemia de coronavirus COVID-19. Para su modelización, incorporaremos variaciones para poder tener en cuenta las medidas de contención que se adoptan. No intentaremos hacer una predicción real con números concretos (en particular, para ello necesitaríamos más datos médicos y políticos de los que nosotros disponemos), sino mostrar la influencia de las medidas en el desarrollo de la epidemia. Sólo queremos mostrar las tendencias cualitativas —con una explicación más o menos técnica de las herramientas matemáticas que se usan en los cálculos y las incertidumbres inherentes al proceso, las mismas que se encuentran todos los epidemiólogos—, no dar previsiones cuantitativas de cómo va a ser el futuro de la epidemia. (Esta entrada es una extracto de un artículo más extenso que se puede consultar completo aquí).
Modelo epidemiológico SEIR
Para nuestra modelización usaremos el modelo SEIR (una adaptación del modelo SIR, que fue propuesto por W. O. Kermack y A. G. McKendrick en 1927). En una población de tamaño fijo \(N\) en la que se ha desatado una epidemia que se propaga mediante contagio, en un tiempo \(t\) los individuos pueden estar en cuatro estados distintos:
Susceptibles: \(S(t)\),
Expuestos: \(E(t)\),
Infectados: \(I(t)\),
Recuperados: \(R(t)\).
El modelo SEIR se adapta bien al comportamiento de la epidemia del coronavirus dado que, en esta enfermedad, además de a los susceptibles de ser infectados, a los ya infectados y a los recuperados, conviene también tener en cuenta a los expuestos, esto es, individuos que portan la enfermedad pero que, al hallarse en su periodo de incubación, no muestran síntomas y aún no pueden infectar a otros (hay que ser precisos con lo que estamos denotando: si un individuo no presenta síntomas pero sí puede contagiar a otros lo contabilizamos en \(I(t)\), no en \(E(t)\)).
En el modelo SEIR tenemos tres parámetros: \(\beta\), llamado tasa de transmisión, de manera que \(1/\beta\) mide la probabilidad de que un susceptible se infecte cuando entra en contacto con un infectado; \(\gamma\), llamado tasa de recuperación, de manera que el periodo medio de recuperación es \(1/\gamma\); y \(\sigma\), de forma que \(1/\sigma\) es el tiempo promedio de incubación. Los dos primeros parámetros definen el parámetro \(R_0=\beta/\gamma\) que se llama tasa básica de reproducción y representa el número de nuevos infectados producidos por un infectado si toda la población es susceptible.
Las ecuaciones diferenciales del modelo SEIR básico son
$$\begin{cases} S'(t) = -\beta S(t)I(t)/N, \\E'(t) = \beta S(t)I(t)/N – \sigma E(t), \\I'(t) = \sigma E(t) – \gamma I(t), \\R'(t) = \gamma I(t).\end{cases}.$$
Modelo epidemiológico para el COVID-19 con medidas de contención
En el caso del coronavirus, bastantes de los estudios ya publicados introducen funciones o ecuaciones adicionales con el objeto de tener en cuenta el comportamiento del inicio de la epidemia en Wuhan en diciembre de 2019, cuando los humanos se infectaban directamente del contacto con animales, así como los desplazamientos extraordinarios de población fruto de las festividades chinas de la época, y otras variables. Prescindiremos aquí de todo eso, y simplificaremos hasta quedarnos con lo que nos parece razonable.
Usando el método SEIR, y siguiendo lo publicado en [1], para modelizar la evolución del coronavirus COVID-19 tomaremos como valor para los parámetros los siguientes: \(\gamma= 1/5\), \(\sigma= 1/7\). Lo más complicado es estimar \(\beta\); en particular, porque no se sabe cuántas personas infectadas asintomáticas hay que puedan estar infectando a otros.
Diversos estudios sobre el comportamiento de la enfermedad en China antes de que se adoptaran medidas drásticas de aislamiento de la población (como el ya citado [1]) sugieren que el valor de \(\beta\) podría estar entre 0.59 y 1.68 (en unidades días\({}^{−1}\)), lo cual daría un \(R_0\) entre 2.95 y 8.4, en ambos casos bastante elevado (un reciente artículo en la revista Lancet [3] toma \(R_0=2.68\)).
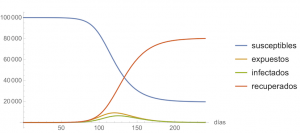
Tomando entonces \(\beta=1\) y suponiendo que tenemos una población de \(100\,000\) personas, en la que hay un infectado al principio, la evolución de la epidemia modelada con las ecuaciones diferenciales del modelo SEIR durante 120 días sería tal como se muestra en la siguiente figura.

Con otros parámetros no muy distintos los valores concretos de las funciones \(S(t), E(t), I(t)\) y \(R(t)\) variarían, pero el aspecto de las gráficas sería similar.
Hasta ahora hemos considerado que la tasa de infección \(\beta\) es constante. Pero este parámetro se puede ajustar artificialmente si se adoptan medidas de contención (protección y aislamiento), y si la población las acepta y las cumple. Así, se han llevado a cabo diversos estudios con parámetros \(\beta\) que van variando en el tiempo. Por ejemplo (véase [2]), con una función decreciente respecto al tiempo de la forma
$$\beta(t) = \beta_0 \Big((c_0-c_b)e^{-r_1t} + c_b\Big)$$
donde \(\beta_0\) sería la tasa de infección sin medidas de contención y las constantes \(c_0\) y \(c_b\) aluden a las tasas de contacto (fruto de los aislamientos de la población); o, también (véase [1]),
$$ \beta(t) = \beta_0 (1-\alpha(t)) \left(1 – \frac{D(t)}{N}\right)^{\kappa},$$
donde \(\beta_0\) es la tasa de infección sin medidas, \(\alpha(t)\) (con valores en el intervalo [0, 1]) es el resultado de las acciones gubernamentales, \(D(t)\) es la sensación pública de riesgo como consecuencia de los casos críticos y muertes conocidos, y \(\kappa\) mide la intensidad de la reacción de los individuos.
Típicamente, \(\alpha(t)\) es una función constante a trozos (las medidas se toman en momentos concretos), y algunas estimaciones (citadas en [1]) sugieren que se puede tomar \(\kappa=1117.3\) (aunque parece un tanto ridículo tomar un valor con cinco dígitos de precisión, ese es el valor obtenido en estudios previos para otras situaciones y, a falta de otra información, es lo que ellos usan).
La idea del factor \((1-D(t)/N)^\kappa\) con un \(\kappa\) elevado es que, cuando la preocupación es mucha, el factor es muy cercano a 0, la gente se aísla incluso voluntariamente y \(\beta(t)\) es muy pequeño; por el contrario, el factor es cercano a 1 y tiene escasa influencia si la preocupación social es poca. Como la realidad político-social china y la occidental no es la misma, difícilmente se puede pensar que podemos usar sus mismos parámetros, pero sí sus mismas ideas de modelización. Como estimación para \(D(t)\) nosotros podemos pensar que el 5% de los casos son graves y, así (sin necesidad de complicar excesivamente las ecuaciones), tomar \(D(t) = 0.05I(t)\) y un \(\kappa\) elevado pero más moderado, digamos, \(\kappa=100\).
Si desde el principio se hubiesen tomado medidas de contención, la evolución de la epidemia hubiera sido muy distinta. Por ejemplo, si, en la ecuación para \(\beta(t)\) anterior \(\beta_0=1\), y \(\alpha(t)\) hubiera tenido el valor constante 0.5, la evolución de la epidemia hubiera sido como se muestra en la siguiente figura.
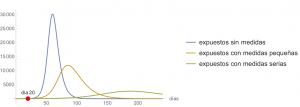
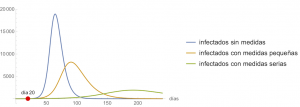
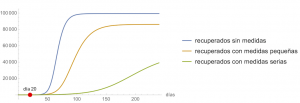
Reiteramos que todo esto son estimaciones, es imposible conocer el futuro, pero sí se puede analizar cómo las medidas afectan a la evolución de la epidemia; en particular, los cambios en el valor de \(\alpha\). Así mostaremos cómo evolucionaría la epidemia en tres escenarios distintos. En concreto, en la figura siguiente se compara cómo cambiaría la evolución de \(S(t)\), \(E(t)\), \(I(t)\) y \(R(t)\) si no se aplicaran medidas de contención (es decir, como en la primera figura) o si estas medidas se comenzaran a aplicar el día 20, es decir con
$$\beta(t) = \begin{cases} \beta_0, & \text{ si $t < 20$},\\ \beta_0 (1-\alpha) \left(1 – {0.05I(t)}/{N}\right)^{\kappa}, & \text{ si $t \ge 20$},\end{cases} $$
con \(\beta_0 = 1.0\) y \(\kappa=100\). A su vez, analizamos dos valores de \(\alpha\) distintos: \(\alpha=0.4\) (medidas pequeñas) y \(\alpha=0.7\) (medidas serias). Está claro que las medidas de contención son realmente efectivas, que permiten suavizar el «pico» y que lo alejan en el tiempo. También, que el efecto de las medidas no es inmediato, sino que tarda días en ponerse de manifiesto. Qué \(\alpha\) va a ser el que se obtiene con unas medidas concretas tomadas por un gobierno es imposible de conocer de antemano, sólo podría ser estimado a posteriori a la vista de lo que haya ocurrido; pero, sea cual sea, su efecto va a ser positivo, y, si en la evaluación diaria de los datos epidemiológicos se ve que no es suficiente para lo que se pretende conseguir, se pueden endurecer las medidas.

Referencias
[1] Qianying Lin, Shi Zhao, Daozhou Gao, Yijun Lou, Shu Yang, Salihu S. Musa, Maggie H. Wang, Yongli Cai, Weiming Wang, Lin Yang, Daihai He, A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action, International Journal of Infectious Diseases 93 (2020), 211–216. Publicado:
March 04, 2020. https://www.ijidonline.com/article/S1201-9712(20)30117-X/fulltext
[2] Biao Tang, Nicola Luigi Bragazzi, Qian Li, Sanyi Tang, Yanni Xiao, Jianhong Wu, An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov), Infectious Disease Modelling 5 (2020), 248–255. Publicado: February 11, 2020. https://www.sciencedirect.com/science/article/pii/S246804272030004X
[3] Joseph T. Wu, Kathy Leung, Gabriel M. Leung, Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study, Lancet 395 (2020), no. 10225, 689–697. Publicado: Jan 31, 2020. https:
//www.thelancet.com/journals/lancet/article/PIIS0140-6736(20)30260-9/fulltext

Buenas! Será posible acceder a el xls con el que se hicieron estos gráficos? Al menos al modelo elemental, sin incluir medidas gubernamentales, etc. Estoy tratando de utilizar el modelo que aquí se explica. Desde ya, muchas gracias
Las gráficas no están hechas con Excel, sino con Mathematica. En el enlace «aquí» al final del segundo párrafo hay un enlace al trabajo completo, y ahí está el código Mathematica para hacer las gráficas.
Buenas noches. Tengo el archivo excel que contiene todos los calculo por si todavia le interesa. Escribame a mi correo maryelgonz@gmail.com
Hola!! Agradecería por favor pudieran compartir el archivo de Excel.
gamartinezch@yahoo.com
Favor de enviarme el archivo Excel a gcorrea@unamad.edu.pe
Hola de Cali, Colombia. También me podrías compartir el excel. mauricio.ledesma@correounivalle.edu.co
Favor de compartir el archivo. Gracias!!!
serias tan amable de compartir tu archivo excel a miliansf@yahoo.es
gracias de antemano
Favor enviar archivo, lmaumm@gmail.com, Excelente análisis. Saludos
Excelente articulo. Agradecería el archivo en excel.
Carlos Guillermo
cbernate@gmail.com
Por favor, puedes compartir tu archivo excel a milenka.ocampo@gmail.com
Muchas gracias!
Saludos
Hola me podrías compartir el archivo en excel, yisus200162@gmail.com
Enviame tu correo y te envio mi modelo en Excel
Buenas, comentar que las personas en período de incubación también producen contagios, lo cual parece no haberse tenido en cuenta.
Por lo demás magnífico!
Se ha tenido en cuenta hasta cierto punto. Pone esto: «(hay que ser precisos con lo que estamos denotando: si un individuo no presenta síntomas pero sí puede contagiar a otros lo contabilizamos en I(t), no en E(t))». Se podía haber hecho un poco distinto y haber puesto en las ecuaciones que tanto los I(t) como los E(t) contagian, con distintos parámetros (en algunos estudios que hemos visto posteriormente hacen algo similar y la los que contagian sin presentar síntomas los llaman A(t), asintomáticos). ¿Pero qué tasas de contagio ponerles? Uno puede pensar que los que están incubando tienen pocos virus y son menos contagiosos (desconozco si eso es así), pero también que los E(t), como están malitos, todo el mundo lo ve y tienen menos contactos. ¿De dónde sacar estimaciones para los parámetros? Necesitaríamos estimar cuánto tiempo pasa un enfermo incubando sin contagiar, incubando contagiando sin síntomas, y ya con síntomas, y cuánto de contagioso es en cada caso. No le vimos sentido a introducir más tipos de personas con más parámetros de los que no podíamos dar ningún valor aproximado, solo inventárnoslo.
Cuanto menor es la tasa de contagio (o mayores las medidas gubernamentales que la regulan a lo largo del tiempo) mayor es la duración de la epidemia, por lo que parece inviable aplicar medidas de aislamiento o distanciamiento social desde un principio. Me equivoco? Y si no me equivoco, es posible que por esta razón muchos gobiernos hayan tardado en tomar estas medidas?
Es verdad, cuantas más medidas, más lento todo. Sin medidas de ningún tipo en ningún país, se podía haber acabado todo en un par de meses, con el 90% de la población mundial afectada y varios cientos de millones de muertos, y con todos los hospitales del mundo colapsados sin posibilidad de atender a la mayoría de los enfermos graves que les llegasen (me estoy inventado las cifras, pero los órdenes de magnitud no serían muy distintos). Eso sí, esto hubiera sido menos perjudicial para la economía, según nos ha explicado algún digno representante del partido republicano de EEUU, a quien le deseo que no tenga a su madre entre los infectados. La razón por la que los gobiernos han tardado en tomar medidas no la podemos saber, pero supongo que es porque no se creían que iba a pasar algo así (tampoco la gente, realmente), y daban prioridad a la lucha política sobre lo que algunos les estaban diciendo que iba a ocurrir (no cancelar las manifestaciones del 8 de marzo debería estar penado con homicidio imprudente, lo mismo que con el mitin de Vistalegre); eran incluso incapaces de mirar a Italia, por ejemplo.
Es un modelo interesante que permite analizar la fluctuación de progreso de la epidemia bajo unos parámetros básicos. indican una comprensión hacia las posibilidades comunes de propagación. Ojalá la gente comprenda la necesidad de estos modelos.
gracias por el artículo, se agradece la difusión. una pregunta que me surge: a la hora de estimar gamma, hay que tener en cuenta tanto recuperados como fallecidos, no? es decir, un posible estimador de gamma sería la media de fallecidos y recuperados al día respecto al stock de infectados?
Excelente artículo… muy necesario para la comunidad científica
Es muy buena propuesta, que pasa cuando los casos son muy pocos y su «aricion» o registro tienes periodos muy largos?
Muy agradecido por publicar el estudio, en muy aleccionador
Estimada doctora apreciaria mucho acceder a la base excel de los calculos de modelamiento. Estoy ensayando posibilidades para el contexto mio
un saludo
carlos
Estoy tratando de correr la sintaxis de su trabajo pero me sale este mensaje y no logro obtener la primera gráfica igual a la suya para luego cambiar los parámetros por lo de mi país
ReplaceAll::reps: {sol} is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing.
Plot::nonopt: Options expected (instead of PlotLegends\[RightArrow]{susceptibles,expuestos,infectados,recuperados}) beyond position 2 in Plot[{sS[t],eE[t],iI[t],rR[t]}/. sol,{t,0,120},PlotRange\[RightArrow]All,AxesOrigin\[RightArrow]{0,0},AxesLabel\[RightArrow]{días,Null},PlotLegends\[RightArrow]{susceptibles,expuestos,infectados,recuperados}]. An option must be a rule or a list of rules.
Juan Carlos, casi seguro que serán cosas del copiar y pegar desde el pdf. Escríbeme un email a jvarona@unirioja.es y te mando el notebook de Mathematica.
Gracias por compartir el trabajo.Es excelente material.
Muchas gracias por este articulo, los muertos no figuran en esta modelizacion?
Me uno a los agradecimientos por este trabajo.
Tengo una duda, en relación con la definicion del parametro beta. El articulo dice: » beta llamado tasa de transmisión, de manera que 1/beta mide la probabilidad de que un susceptible se infecte cuando entra en contacto con un infectado». En otro momento se le llama con el nombre, ligeramente distinto, de «tasa de infección». Y en otra parte del articulo se dice que «1/beta es el tiempo típico entre contactos»
Mis preguntas son: (1) ¿cómo puede beta tomar valores menores que 1 si su inverso mide una probabilidad? (ref. página 4 del articulo) (2) ¿es o no beta el inverso de una magnitud temporal (como parece el caso en los otros 3 parámetros del modelo SEIR, cuyos inversos se miden en días)?
Un gran trabajo. Gracias por compartir su codigo, he tatado de replicar la primera grafica sin lograrlo, al correr el script, me arroja el siguiente error:
Syntax::bktmop: Expression «NDSolve[{sS'[t]==-beta0*sS[t]*iI[t]/nN,eE'[t]==beta0*sS[t]*iI[t]/nN-sigma*eE[t],iI'[t]==sigma*eE[t]-gamma*iI[t],rR'[t]==gamma*iI[t],sS[0]==nN-iI0,eE[0]==I0,iI[0]==0,rR[0]==0},{sS,eE,iI,rR},{t,0,240}];
<>]» has no opening «[«.Plot::nonopt: Options expected (instead of PlotLegends\[RightArrow]{susceptibles,expuestos,infectados,recuperados}) beyond position 2 in Plot[{sS[t],eE[t],iI[t],rR[t]}/. sol,{t,0,120},PlotRange\[RightArrow]All,AxesOrigin\[RightArrow]{0,0},AxesLabel\[RightArrow]{días,Null},PlotLegends\[RightArrow]{susceptibles,expuestos,infectados,recuperados}]. An option must be a rule or a list of rules. Debe ser error de sintaxis.Por favor me podria ayudar, toda vez que necesito hacer este analisis con los datos de mi pais. De antemano muchas gracias
¡Muy motivador! Agradesco su tiempo y la forma tan didáctica de exponernos el Modelo SEIR.
Estimada Dra. Les felicito por la excelente presentación, muy clara y didactica le agradeceria me hiciera llegar el archivo excel para poder aplicarlo a la realidad de mi región. Desde ya se agradece, cordiales saludos
Buenas
Podrían por favor compartirme el Excel, agradecido por los aportes.
Excelente explicación del modelo, favor le solicito me pueda compartir el excel del modelo.
ME PUEDEN ENVIAR EL EXCEL
Muy buena explicación.
Por favor podría compartir su archivo excel al correo: lualvega@hotmail.com
Por favor compartir el archivo excel a oscarmartinezmichel@gmail.com