Covid-19: confinar cuanto antes ayuda a salvar vidas (actualizada 26 marzo)

Actualización 26 de marzo

Las estimaciones de esta entrada se hicieron con datos del 18 de marzo. Datos actualizados muestran que nuestras estimaciones para el número de muertes por Coronavirus en España dieron valores inferiores a los que vendrán. Nuestra estimación más optimista, de \(1\,500\) muertes, ya ha sido ampliamente superada y todo parece indicar que incluso la más pesimista, de \(8\,000\), se quedará corta. Como ya advertíamos, lo importante no era esa cuantificación, sino lo que implicaban los datos: la importancia de anticiparse en la adopción de medidas de confinamiento por parte de los gobernantes y de cumplirlas con rigor por parte de la población. La mayor gravedad de la epidemia que muestran los datos actualizados viene a confirmar e incluso a reforzar esa enseñanza: tenemos que cumplir con severidad el confinamiento.

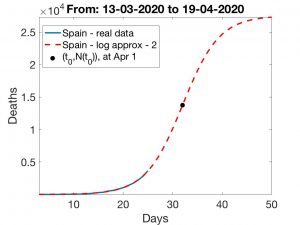
Sospechamos que el número de muertes de los últimos días indican que la curva logística, que tan bien funciona para China, quizá no sea tan adecuada en España. Ignoramos qué puede explicar esta diferencia, pero es posible que la acumulación de muertes en las residencias de ancianos, que se ha detectado en varias Comunidades Autónomas (en algunas de las cuales da cuenta del 50% de los fallecidos), puede estar introduciendo un sesgo, quizá temporal pero importante en la distribución logística. Si ese es el caso, las predicciones están muy condicionadas por la evolución separada del número de muertes que se localice en esos centros los próximos días y por el tiempo que tarde en corregirse ese sesgo (o sea, cuánto tiempo se tarde en controlar las infecciones en las residencias). Con este escenario, el margen de error de las predicciones aumenta (al depender más de los resultados de actuaciones decisivas que se están llevando a cabo estos días y en los próximos).  De esta forma, poco se puede decir sin más supuestos adicionales, como por ejemplo suponer que esté próximo en el tiempo el día en que la curva logística alcance su punto de inflexión, lo que los epidemiólogos llaman el pico de infección. Así, y suponiendo que no se corrija el sesgo producido por las muertes en las residencias, nuestras estimaciones apuntan a que si el pico se alcanzase el 29 de marzo (una predicción quizá demasiado optimista), tendríamos entre \(14\,000\) y \(19\,800\) muertes hacia el 19 de abril; si se alcanzara tres días después, el 1 de abril, las muertes podrían estar entre \(26\,500\) y \(51\,000\) para el 19 de abril. Incluimos detalles y gráficas al final de la entrada.

(Sigue el texto de la entrada publicada el 18 de marzo)

En esta entrada presentaremos estimaciones de las cifras de muertes por coronavirus en España para varios supuestos sobre la fecha de entrada en vigor de las acciones de aislamiento. Tomaremos como test la evolución del número de muertes en China (donde la situación se da por estabilizada) y seguiremos métodos muy simples, parecidos a los que ha implementado B. Marcos, de la Université Côte d’Azur, para los datos de Francia (véase [1]).

Debemos advertir que, dadas las evidentes diferencias entre las características de China (número de habitantes, extensión, situación política, etc.) y España y dado el carácter elemental de las técnicas y las hipótesis que siguen, las estimaciones aquí ofrecidas indican más órdenes de magnitud que valores reales. El objetivo que pretendemos no es tanto acertar en la estimación como cuantificar la influencia que tiene en la evolución del número de muertes producidas por la epidemia adoptar rápidamente medidas enérgicas de confinamiento.

En un período inicial, la evolución \(N_i = N_i(t)\) del número de muertes de una epidemia suele seguir un comportamiento exponencial. Por tanto, se suele modelar en la forma

$$N_i(t)=ae^{t/\tau},$$

donde \(\tau\) y  \(a\) son parámetros de ajuste, que se interpretan como propiedades de la población afectada. La variable \(t\) corresponde al tiempo, medido por ejemplo en días.

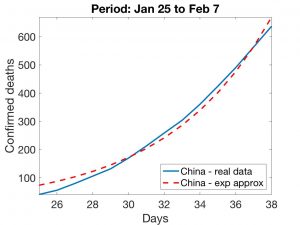
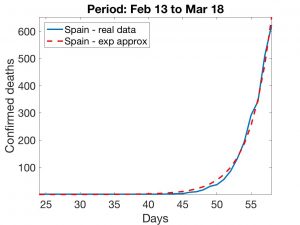
En las Figuras 1 y 2, mostramos ajustes exponenciales para los datos iniciales chinos y españoles.

En los fenómenos epidemiológicos de este tipo, una vez aplicadas medidas de contención, podemos aproximar la evolución posterior del número de muertes con una distribución logística del tipo

$$N(t)=\frac{k}{1+e^{-\frac{t-t_0}{\tau}}}.$$

Aquí aparece un parámetro importante, \(t_0\), que tiene la dimensión del tiempo e indica el instante de inflexión en la evolución del número de muertes (la derivada segunda de \(N\) se anula \(t_0\) y solo en \(t_0\)). El parámetro \(\tau\) es análogo al que aparece en \(N_i\) y \(k\) se puede ajustar de varias formas, por ejemplo haciendo coincidir las curvas determinadas por \(N_i\) y \(N\) en un día prefijado en la secuencia de datos.

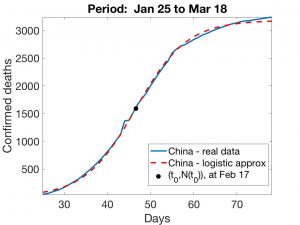
En el caso de China (que servirá de test), se documenta la primera víctima en Wuhan el 9 de enero y el bloqueo se decretó para la provincia China de Hubei el 23 de enero (14 días después). A partir de los datos chinos, se pueden conseguir curvas logísticas de ajuste muy aceptables por dos métodos distintos:

• 

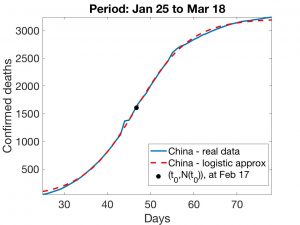
  Fijamos el valor de \(\tau\) determinado por el ajuste exponencial (Figura 1) y calculamos \(k\) y \(t_0\) de modo que los valores de \(N\) en los días que van del 25 de enero al 17 de marzo minimicen, en el sentido de los mínimos cuadrados, la distancia a los valores conocidos. El resultado aparece en la Figura 3.

• Dejamos libres los valores de \(\tau\), \(k\) y \(t_0\) y resolvemos el problema de mínimos análogo. Puede observarse la curva resultante en la Figura 4.

Se observa que las curvas conseguidas son casi coincidentes. Esto da credibilidad al cálculo de \(t_0\), que corresponde aproximadamente al 17 de febrero (39 días después de iniciado el ciclo de muertes, 25 días después del inicio del confinamiento).

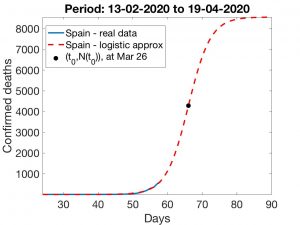
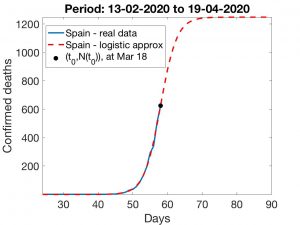
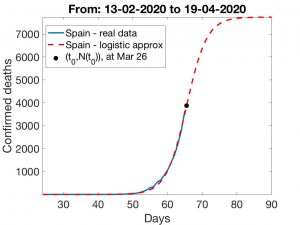
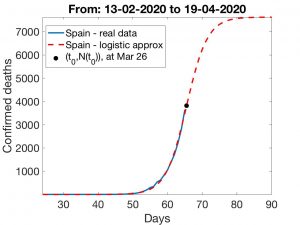
En España, el estado de alerta empezó a funcionar el 15 de marzo (32 días después del primer fallecimiento). Con las técnicas que preceden, se obtienen las curvas de ajuste logísticas visualizadas en la Figuras 5 y 6. Los resultados observados en la primera son bastante pesimistas: el \(t_0\) calculado corresponde al 26 de marzo y el número de muertes seguirá creciendo hasta llegar aproximadamente a 8500. Los resultados que proporciona la segunda técnica son más esperanzadores: estamos ya llegando al instante de inflexión (entre el 18 y el 19 de marzo) y el número de muertes será algo inferior a 1300. Un resultado intermedio resulta de usar el primer método anterior, pero ajustando al periodo 3 al 17 de marzo (descartando el periodo 13 de febrero al 2 de marzo en el que el número de muertes se mantuvo constante igual a uno); en este caso el número final de muertes rondaría los 3.000.

Desgraciadamente, todavía no tenemos suficientes datos para decir con seguridad más cosas.

Lo que sí podemos hacer es  comparar la situación actual con la que podríamos tener si las medidas de confinamiento se hubieran tomado antes, pongamos el 10 de marzo (cuando se empezaron a cerrar colegios y universidades en Madrid, País Vasco y La Rioja).

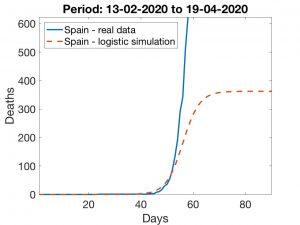
Con un \(t_0\) 10 unidades inferior al que corresponde a la Figura 5, conservando el valor de \(\tau\) y ajustando el valor de \(k\) para que el número de muertes coincida con el número real a principios de marzo, obtenemos la curva mostrada en la Figura 7. Se observa que, ahora, el máximo de fallecimientos es aproximadamente 370, alrededor de 20 veces menos que la estimación pesimista (Figura 5) y menos de un tercio de lo previsto en la estimación optimista.

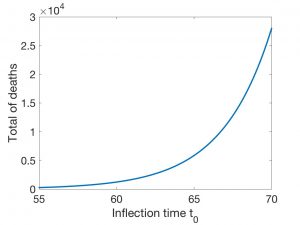
Así, el número total de muertes se ve enormemente influido por la fecha en la que da comienzo el confinamiento. En realidad se puede estimar el número final de muertes en función de  \(t=t_0\) (y por tanto en función de la fecha en que se tomen las medidas de confinamiento); véase la Figura 8.

Referencias

[1] B. Marcos, Prédiction du nombre de malades de COVID-19 en fonction de la date du confinement en France,

https://math.unice.fr/~marcos/coronavirus.pdf

[2] M. Roser, H. Ritchie, E. Ortiz-Ospina, Coronavirus Disease (COVID-19) – Statistics and Research, https://ourworldindata.org/coronavirus

Actualización 26 de marzo

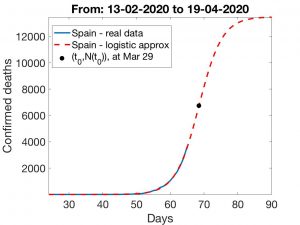
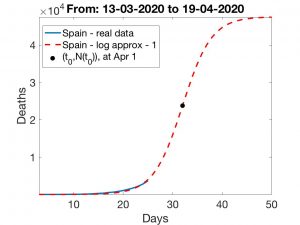
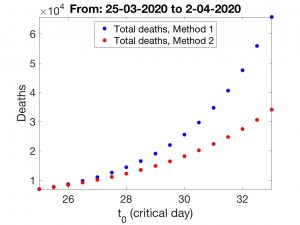
En las Figuras que siguen, indicamos qué escenarios corresponden a los días de inflexión 26 de Marzo, 29 del mismo mes y 1 de Abril. Indicamos en cada caso el número total de muertes \(k\). Como es lógico, las previsiones correspondientes a los Métodos 1 y 2 difieren a medida que \(t_0\) crece. Finalmente, mostramos en la Figura a la derecha el modo en que \(k\) crece a medida que lo hace el valor de \(t_0\). Con independencia del efecto que puede tener el incremento de muertes en residencias de la tercera edad, la conclusión siempre es la misma: aplicar rápidamente medidas de confinamiento es crucial para «adelantar» la fecha del día crítico lo cual, a su vez, es imprescindible para que los efectos de la epidemia sean lo menos dañinos posible.