Cuidado con el panadero y con los vocales de la mesa electoral . . .

Esta entrada tiene como objetivo mostrar en qué modo el número de contactos entre personas influye sobre la propagación de una epidemia. También, que basta con que haya algunas personas «populares», que tengan relación con muchas otras, para que la velocidad de propagación crezca muy peligrosamente. Finalmente, que el confinamiento tiene pleno sentido para combatir y superar una crisis como ésta. Se proponen ejercicios sobre el coronavirus para estudiantes de todos los niveles de dificultad creciente, Se aconseja atacarlos progresivamente, no demasiados a la vez, para no desmotivarse.

¿De qué depende la propagación?

La velocidad de propagación de una epidemia depende de varios factores:

• La sociabilidad (la frecuencia de contactos entre individuos).

• La intensidad de contagio (la probabilidad de transmisión entre personas que contactan) y los medios de protección.

Conviene por tanto desarrollar estrategias para reducir la peligrosidad de los contactos y su número. De hecho, veremos a continuación que, más que la sociabilidad media, lo que realmente cuenta es la presencia de personas muy sociables.

Difusión de un virus en un grupo homogéneo

Consideremos un grupo, \(H_1\), de \(1000\) personas. Se supone que cada una de ellas tiene \(10\) contactos diarios con otras personas y que la probabilidad de contagio es \(0.1\).

Cada persona infectada contacta otras \(10\) y de éstas una es infectada. Luego cada infectado ha dado lugar a un nuevo infectado cada día. A partir de una sola persona infectada, tenemos por tanto:

• Día 1: \(1+1 = 2\) infectados.
• Día 2: \(2+2 = 4\) infectados.
• Día 3: \(4+4 = 8\) infectados.
• Día 4: \(8+8 = 16\) infectados, etc.

Cada día doblamos el número de infectados. El día \(n\) habremos llegado a \(2^n\) infectados (la famosa ley exponencial de la que tanto hablan los medios estos días).

Difusión en presencia de personas «populares»

Consideremos ahora el grupo \(P\), conseguido al añadir a \(H_1\) otras \(10\) personas muy populares que tienen contacto cotidiano con todos. Entonces, de nuevo a partir de una sola persona infectada, obtenemos:

• Día 1: El infectado contacta con \(10\) personas e infecta a una de ellas y también a uno de los \(10\) miembros populares, dado que todos ellos contactan con él. Tenemos \(1+1+1 = 3\) infectados.

• Día 2: El popular enfermo infecta a la décima parte de las \(1000\) personas con las que tiene contacto. Por otra parte, los otros dos enfermos infectan dos nuevos populares y dos personas más. Tenemos ahora \(100 + 3 + 4 = 107\) enfermos, de los cuales \(3\) son populares.

• Día 3: Los \(3\) populares enfermos infectan a \(3 \times 100 = 300\) personas. Por otra parte, los _\(104\) enfermos restantes pasan la enfermedad a otros \(104\) y a todos los populares sanos que quedaban. Tenemos: \(300 + 104 + 7 = 411\) infectados y todos los populares forman parte de este colectivo.

• Día 4: Todos los individuos son infectados.

Así, en \(4\) días, tenemos toda la población enferma, contrariamente  a los  \(2^4\) que obteníamos en el caso del grupo \(H_1\).

Primeras conclusiones

No pretendemos describir la realidad con estos ejemplos. Tan solo sirven para ilustrar la gran importancia que tienen las personas muy sociables, las  que contactan frecuentemente con muchas otras.

Es fácil identificar algunas de estas personas. Basta pensar en la que está a cargo de la caja de un supermercado o la que nos atiende en la panadería … y en el vocal de una mesa electoral. Si veis que no llevan mascarilla ni guantes y los tenéis a mano, regaládselos.

Conclusión 1: Es esencial que las personas que poseen contactos cotidianos múltiples estén muy bien protegidas para que no enfermen e infecten a otras: que estén bien lejos de los clientes, que se cubran el rostro y enfunden sus manos, etc. Conviene recordárselo si se les olvida.

Conclusión 2: El sistema electoral francés (a dos vueltas) es un medio muy eficaz para difundir un virus: en la primera vuelta, los vocales de mesa quedan infectados; en la segunda, distribuyen el virus.

Ejercicios sencillos

Ejercicio 1: ¿Cuántos enfermos habrá en una semana en el grupo \(H_1\)? ¿Y en dos semanas?

Ejercicio 2: ¿Al final de cuántos días estarán las \(1000\) personas del grupo \(H_1\) enfermas?

Ejercicio 3:  Responder a las mismas preguntas para un grupo \(H_2\) de \(1000\) personas donde el número de contactos diarios es de \(5\) por persona, con probabilidad de contagio \(0.2\). Comparar con los resultados obtenidos para el grupo \(H_1\).

Ejercicio 4: Mismo enunciado para un grupo \(H_3\) de \(1000\) personas, cada una con \(2\) contactos diarios con otras \(10\), suponiendo de nuevo que la probabilidad de contagio es \(0.1\).

Ejercicio 5: También, para un grupo \(H_4\) de \(10000\) personas que se comportan como las del grupo \(H_1\).

Confinando la población

Volvamos a considerar nuestro grupo homogéneo \(H_1\). Supongamos que, como antes, se ha propagado el virus a partir de una persona infectada y han pasado ya \(n\) días. Claramente, si no se hace nada, acabarán todos enfermos.

Pero en ese grupo hay alguien inteligente y con capacidad de persuasión: nuestro amigo \(h\). Se da cuenta de que un individuo que haya sido infectado y se queda en casa, si se abstiene de acercarse a cualquier otra persona, se recupera totalmente a los \(p\) días. Entonces envía un mensaje a los otros miembros del grupo y convence a unos cuantos de que se recluyan.

¿Qué ocurrirá a partir del día \(n+1\)? ¿Y el día \(n+p\)? ¿Y más tarde?

Claro, la respuesta depende de cuántos se han dejado convencer:

• Si \(h\) fue capaz de convencer a los \(2^n\) infectados, éstos se van a casa y al cabo de \(p\) días están sanos. Como no quedó ningún enfermo fuera, asunto acabado.

• Por el contrario, si \(h\) no convenció a uno de los \(2^n\), digamos el ciudadano \(k\), estamos perdidos.

En efecto, no hay ninguna razón por la cual \(k\) deje de relacionarse con los demás. Tal vez, un poco alarmados por las palabras de \(h\), cada miembro no recluido de \(H_1\) contacta con \(5\) y no \(10\) personas cada día (la mitad). Pero eso significa que todo enfermo genera un nuevo enfermo cada dos días. Así, razonando como antes, vemos que al cabo de \(m\) días habrá \(2^{[m/2]}\) personas infectadas.

Cuando haya transcurrido mucho tiempo, solo los \(2^n – 1\) individuos que se refugiaron sobreviven (y esto suponiendo que tras pasar la enfermedad quedan inmunes).

Si no es posible confinar todos los enfermos, parece inteligente diseñar una estrategia basada en retirar de la vida en sociedad, al menos, un número determinado de  ellos periódicamente, cada cierto tiempo. Si suponemos  de nuevo que los recuperados no vuelven a ser susceptibles y el confinamiento se produce con suficiente frecuencia y afecta a un número suficientemente alto de individuos, acabaremos erradicando la enfermedad.

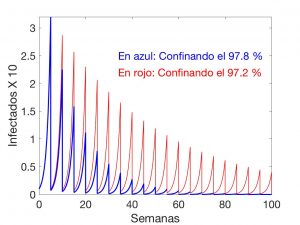
La evolución del número de enfermos seguirá muy aproximadamente una curva como las que aparecen en la Figura que precede. En el caso de la curva azul, cada \(5\) semanas el \(97.5 \%\) de los enfermos queda confinado. Vemos que la enfermedad desaparece en poco más de un año.  Por el contrario, si bajamos el porcentaje de infectados en cuarentena al \(97.2 \%\) (curva roja), pasados dos años todavía estaremos sufriendo la enfermedad a un nivel no despreciable.

En grandes poblaciones, el confinamiento frecuente de grupos numerosos es muy complicado (por no decir imposible). Sin embargo, no resulta descabellado imponer esta estrategia durante un tiempo limitado, a la espera de que lleguen remedios más efectivos y, en particular, dispongamos de vacunas.

Por otra parte, el efecto que produce aplicar periódicamente una terapia efectiva a un alto porcentaje de la población es similar. De nuevo, la evolución de la enfermedad queda descrita por una curva como las de la Figura.

Conclusión 3: Conviene hacer caso de las normas que, poco a poco, van siendo impuestas en todas partes: ciudadanos y ciudadanas, id a casa, divertíos todo lo que podáis en familia, aprovechad para leer, aprender cosas nuevas y cuidar las plantas, pero no salgáis a menos que sea estrictamente necesario hasta que se os diga.

Ejercicios algo más difíciles

Ejercicio 6: Responder a las preguntas de los Ejercicios 1 y 2 para un grupo \(X\) de \(n\) personas, cada una de las cuales efectúa \(c\) contactos diarios, de manera que la probabilidad de transmitir el virus en cada contacto es \(p\) (naturalmente, \(0 \leq p \leq 1\)). Verificar que se vuelven a conseguir los resultados de los Ejercicios anteriores.

Ejercicio 7:  Responder a las preguntas de los Ejercicios 1 y 2 para el grupo \(C\) (con enlaces).

Ejercicio 8: ¿Por qué los cálculos realizados en los Ejercicios 1 y 2 son (un poco) falsos?

Indicación: Cuando una persona está enferma y las \(10\) personas que contacta están ya enfermas, ¿cuántos nuevos enfermos genera? Por otra parte, ¿debemos contar dos infectados más cuando una persona sana atrapa dos veces la enfermedad?

Ejercicio 9: Hallar estimaciones (superiores e inferiores) de los números de enfermos que deben ser calculados en los Ejercicios 1 y 2. Generalizar las ideas y determinar, si es posible, estimaciones en la situación general abordada en el Ejercicio 6.

Indicación: Para comprender bien la situación, comenzar con un grupo de (por ejemplo) \(10\) personas, cada una con \(2\) contactos diarios, con probabilidad de contagio \(0.5\).

Ejercicio 10: Consideremos de nuevo el grupo \(X\) del Ejercicio 6. Sabemos que un enfermo aislado se cura a los \(m\) días y que, tras pasar la enfermedad, queda inmune. Por otra parte, cada vez que se produce un confinamiento, el número medio de contactos diarios de los miembros queda multiplicado por \(0.75\) (es decir, se reduce a las tres cuartas partes). Se quiere aplicar una estrategia similar a la que se describe en la Sección precedente, confinando \(g\) personas del grupo de infectados cada \(d\) días. Fijamos un plazo máximo de \(D\) días para erradicar totalmente la enfermedad. ¿Qué condiciones deben cumplir \(g\) y \(d\) para alcanzar este objetivo? De entre todas las elecciones posibles, ¿cuál es la más «barata», esto es, la que corresponde al mayor valor de \(d\)?