El amor en los tiempos del corona

“Mathematics is everywhere” fue el lema elegido por la UNESCO para celebrar el Día Internacional de las Matemáticas de 2020. Desafortunadamente, las matemáticas no estuvieron presentes en los primeros momentos de la crisis del coronavirus COVID-19: nuestras autoridades consideraron, sin el aval de modelos matemáticos, que no era mala idea permitirnos acudir arrimaditos a manifestaciones, partidos de fútbol y besapiés.

Ahora, desde nuestro confinamiento, oímos a matemáticos, profesionales o aficionados, hablar en los medios de estimaciones del erre cero y de proyecciones que deben estar, como también deberían haber estado antes, presentes en la toma de decisiones sobre salud pública.

Гео́ргий Феодо́сьевич Вороно́й, es decir, Voronoi, falleció en 1908 sin saber nada del COVID-19 y sin saber, por tanto, que este alteraría sustancialmente nuestra forma de relacionarnos y, ya lo veremos, de amarnos. Quizás su legado nos ayude a hacer más eficaz, aunque no más llevadero, el distanciamiento social que -ahora sí- ejercemos, ayudándonos a responder a estas dos preguntas:

1. ¿Dónde debería ubicarme en una región R poligonal (una sala de trabajo, un ascensor, el pasillo del papel higiénico en el supermercado…) para maximizar la distancia (euclídea) que me separa de las demás personas de un conjunto P?
2. ¿Cómo deberían distribuirse en esa misma R las personas de P de modo que la mínima distancia de separación entre ellas fuera máxima?

La primera pregunta tiene una respuesta fácil y de rápida implementación, pues el tiempo de ejecución algorítmica crece subcuadráticamente con el cardinal de P. Solo necesitamos saber que la distancia euclídea, como toda distancia inducida por una norma, es una función convexa, y por tanto alcanza su máximo sobre un compacto en algún punto extremo, y también necesitamos saber qué es un diagrama de Voronoi, pero eso ya lo sabemos, pues alguna vez nos lo ha explicado, y muy bien explicado, nuestra Clara Grima. En pocas y toscas palabras, el diagrama de Voronoi del conjunto P de n puntos del plano es la subdivisión del plano en n celdas, donde la celda V(k) asociada al punto k es el lugar geométrico de los puntos del plano que están más cerca de k que de los demás puntos de P. Cada celda V(k) está definida como intersección de semiplanos cerrados (los que tienen de frontera las mediatrices de un punto con todos los demás) y son, por tanto, polígonos convexos. Para determinar mi ubicación en una región R poligonal maximizando la mínima distancia a los puntos de P basta construir el diagrama de Voronoi de P e intersecar cada celda V(k) con la región R, obteniendo así una subdivisión de R en polígonos V*(k); sobre cada V*(k), el punto más cercano a mí es k, por lo que maximizar la distancia al punto más cercano es maximizar la distancia a k, cosa que consigo ubicándome en cierto punto extremo del polígono V*(k). En definitiva, encuentro mi ubicación óptima evaluando un conjunto finito de puntos de cardinal muy bajo y fácil de generar.

Mientras que la pregunta 1 se refiere a una decisión individual (¿dónde me ubico?), la pregunta 2 conlleva una decisión colectiva: ¿dónde nos ubicamos?. Por mucho que pese a los liberales, la decisión óptima para la colectividad no necesariamente se genera a partir de decisiones individuales óptimas. En efecto, si pudiéramos decidir cómo distribuir n personas en R, podríamos buscar una configuración inicial, por ejemplo, aleatoria, y después aplicar secuencialmente el procedimiento descrito arriba, buscando para cada punto su ubicación óptima suponiendo que los demás permanecen fijos, y ya sabemos que basta considerar como candidatos los vértices del diagrama de Voronoi correspondiente. Este procedimiento, aplicado a cuatro personas a ubicar en un cuadrado R, podría converger a la configuración de la figura 1 (izquierda), en la que nadie tiene incentivo para moverse individualmente; sin embargo, la decisión colectiva mostrada en la figura 1 (derecha) separa más, bastante más, a todos.

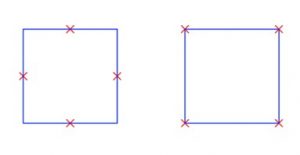
Salvo que seamos unos irresponsables, no deberíamos quedarnos satisfechos con una solución óptima local o punto de equilibrio del problema 2: deberíamos buscar una solución óptima global. Las condiciones usuales de optimalidad (las de Karush-Kuhn-Tucker) son en este caso necesarias pero no suficientes, así que, para resolver de verdad este problema de optimización cuadrática no convexa, tendremos que recurrir al ordenador. Resolver numéricamente problemas de optimización como este puede privarnos de matemáticas elegantes (hay pocas herramientas teóricas, las propiedades analíticas son pocas y endebles, es difícil generar teoremas y teorías), pero tenemos, en cambio, matemáticas eficaces.

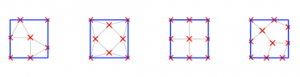
Por si fuera de interés, en la Figura 2 adjunto configuraciones que maximizan la distancia mínima entre n puntos (n=7,8,9,10) en un cuadrado R, que podría ser la cabina de un ascensor de los grandes. He marcado con líneas delgadas los pares de puntos que están más próximos. Estemos especialmente vigilantes a sus micropartículas. De todos modos, será mucho mejor para todos (otra decisión colectivamente óptima) olvidarse del ascensor y aplicar de verdad el lema #YoMeQuedoEnCasa