Solución: Triángulos pasteleros

Publicamos la solución al divertimento de los triángulos pasteleros. Gracias a Jaime Benabent, Gustavo Roque Collado, Antonio Navas, Miguel Pineda y Enrique Zubiría por las soluciones que nos han enviado.

Divertimento:

En una pastelería se elaboran tartas triangulares cuyo precio depende exclusivamente de su peso. Tienen cuatro tamaños distintos, obteniéndose todos ellos de la pieza mayor, representada en la imagen por el triángulo \(ABC\).

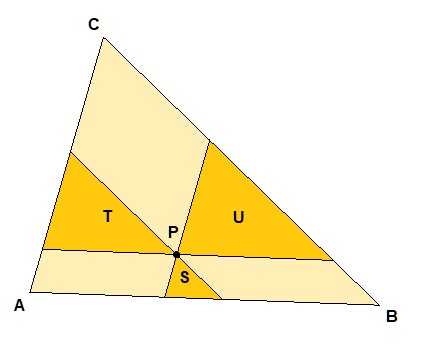
El resto de piezas se consigue eligiendo un punto \(P\) interior a dicho triángulo y haciendo tres cortes paralelos a los lados pasando por \(P\). Si los precios de las tres porciones menores son \(S\), \(T\) y \(U\), ¿cuánto costará la tarta grande?

Solución:

Como trazamos paralelas a los lados del triángulo pasando por \(P\), cada uno de los triángulos pequeños será semejante a \(ABC\) por ser sus ángulos correspondientes iguales, por lo que denotando \(V\) al precio del triángulo grande (que será proporcional a su área si asumimos que la tarta es de densidad y altura constante), existirán tres constantes de semejanza \(\lambda\), \(\mu\) y \(\nu\) tales que
$$S=\lambda^2V,\,T=\mu^2V \text{ y } U=\nu^2V.$$

Es más, si respectivamente, llamamos \(Q\) y \(R\) al corte de la recta paralela a \(AB\) que pasa por \(P\) con los lados \(AC\) y \(BC\) y \(X\) e \(Y\) a los cortes del lado \(AB\) con las rectas paralelas a \(AC\) y \(BC\) pasando por \(P\), también tendremos que
$$QP=\lambda AB,\,PR=\mu AB, \text{ y } XY=\nu AB.$$
Ahora bien, por ser \(AXPQ\) e \(YBRP\) dos paralelogramos, \(AX=QP\) e \(YB=PR\), con lo que \(QP+XY+PR=AB\). Reuniendo todo lo anterior, obtenemos el siguiente sistema de ecuaciones:
$$\left\{\begin{array}{l}
S=\lambda^2V\\
T=\mu^2V\\
U=\nu^2V\\
\lambda+\mu+\nu=1
\end{array}\right. $$
Este sistema tiene como única solución
$$\lambda=\frac{\sqrt{S}}{\sqrt{S}+\sqrt{T}+\sqrt{U}},\, \mu=\frac{\sqrt{T}}{\sqrt{S}+\sqrt{T}+\sqrt{U}} \text{ y } \nu=\frac{\sqrt{U}}{\sqrt{S}+\sqrt{T}+\sqrt{U}},$$
y por lo tanto,
$$V=\left(\sqrt{S}+\sqrt{T}+\sqrt{U}\right)^2.$$