La crisis desatada por el SARS-CoV-2 nos hace hablar de los respiradores, unos aparatos específicos, imprescindibles en las Unidades de Cuidados Intensivos (UCI), capaces de sustituir o ayudar a los pulmones en su función. Un paciente con insuficiencia respiratoria necesita un respirador para vivir. Y, como sabemos, precisamente la incapacidad para ventilar u oxigenarse está siendo una de las consecuencias que produce el COVID-19.

Fabricar respiradores se ha convertido en un asunto de interés general. En las últimas semanas, ha crecido fuertemente el número de iniciativas. En España, aparte de las empresas del sector (Temel en Valencia, Hersill en Madrid), se han estado o están fabricando en plantas de Seat (Martorell), Fujitsu Ten (Málaga), Airbus (Sevilla), entre otras. También, numerosas universidades de todo el mundo se han involucrado en esta actividad. Entre muchas otras, citaré aquí la Universidad Federal de Paraíba (Joao Pessoa, Brasil), donde un grupo de profesores ha conseguido diseñar una máquina de montaje rápido, precio muy asequible y, entre otras ventajas, acceso remoto.
Dräger, la cerveza y los respiradores

Los primeros respiradores fueron fabricados por la compañía Dräger.
Fundada inicialmente como Dräger & Gerling por J. Heinrich Dräger y C.A. Gerling en 1889, tuvo como primer objetivo mejorar los sistemas de embotellamiento de cerveza. Desde la segunda mitad del siglo XIX, ya era posible rellenar tanques de acero con gas a presiones elevadas. Sin embargo, eliminar el gas de forma segura y controlada constituía un serio problema. Frecuentemente, el proceso era defectuoso y ocasionaba daños.
En esos años, Dräger y su hijo Bernhard inventaron, patentaron y empezaron a fabricar la válvula Lubeca que, por primera vez, permitía controlar con exactitud la cantidad de dióxido de carbono que debía ser eliminada en los tanques de alta presión.

Posteriormente, bajo el impulso de Bernhard Dräger, la compañía adoptó el lema Tecnología para la vida y centró sus intenciones en desarrollar actividades innovadoras al servicio de la salud y, más precisamente, el uso del oxígeno con fines médicos. A partir de1899, la compañía lanzó al mercado distintos productos: máquinas, válvulas de reducción, manómetros de alta presión, etc. En particular, aparece en 1907 el Pulmotor, el primer respirador artificial. Esta máquina, capaz de crear alternativamente presiones positivas y negativas, fue usada con éxito como un «resucitador» portátil en la industria minera; véase la Figura 3.
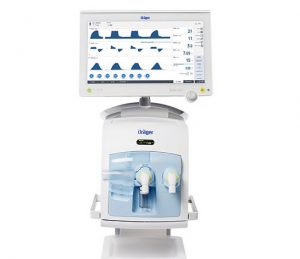
Los fundamentos de un respirador han sido siempre los mismos. Con oxígeno y aire medicinal, el mezclador interno genera una concentración de gas que es suministrada al paciente. En todo momento se controla que la mezcla sea la adecuada mediante un sensor de oxígeno. Lo que se pretende es conseguir una evolución que vaya de una ventilación totalmente controlada a la respiración espontánea y autónoma. Como es lógico, para esto se ha ido recurriendo a respiradores dotados de una tecnología cada vez más sofisticada.
El respirador más moderno del presente, también fabricado por Dräger, es el Evita V800. Fue diseñado este mismo año para tratar las patologías más graves y, a pesar de que su lanzamiento no estaba previsto hasta mediados de 2020, está siendo instalado en la actualidad en algunas UCIs españolas. Entre otros avances, el Evita V800 es capaz de personalizar la terapia y reducir considerablemente la estancia hospitalaria con una pronta desconexión del soporte respiratorio.
El HEV

En fechas recientes, se ha tenido noticia de un interesante proyecto lanzado e iniciado en el CERN.
Los sistemas utilizados para regular el flujo de gas en experimentos de detección de partículas en el Large Hadron Collider (LHC), el mayor acelerador del mundo, poseen características estructurales y funcionales muy similares a las de los modernos respiradores. Esta observación ha permitido diseñar una nueva máquina, el High Energy physics community Ventilator (HEV).
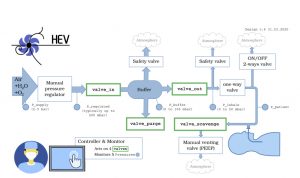
El funcionamiento del HEV obedece al esquema presentado en la Figura 6: la unidad toma en entrada el suministro habitual de aire comprimido o mezclado; la presión suministrada es reducida aproximadamente a la décima parte por un regulador; durante la fase expiratoria, se procede al llenado de un compartimento de aproximadamente 2 litros, controlado por una válvula de entrada, hasta conseguir una presión deseada; a continuación, se cierra esta válvula, se comprueba si el valor de la presión es correcto y, acto seguido, se abre la válvula de salida, iniciándose así el ciclo respiratorio; tanto el ritmo de respiración, como el tiempo de inspiración (que corresponde al momento en que la válvula de salida queda abierta) y el tiempo de parada son controlables; si se fija un valor positivo para la presión pulmonar en el instante final de expiración, este valor es alcanzado.
Esta descripción justifica la analogía del respirador diseñado y los reguladores de gas del LHC.

El prototipo fue culminado a finales de marzo y será probado próximamente en hospitales. En principio, se quiere utilizar en pacientes cuyo estado sea como mucho grave pero no crítico o estén en fase de recuperación; esto permitirá dejar libres respiradores más sofisticados para casos especiales. Como ventajas adicionales, señalemos que el diseño se basa en elementos abundantes y poco costosos y que el programa instalado y el resto de sus componentes consumen poca energía. Eventualmente, puede ser alimentado con baterías, paneles solares, grupos electrógenos, etc. y esto hace de él un respirador idóneo para zonas de recursos limitados.
En lo que se refiere a previsiones de producción, es intención del CERN, por una parte, poner el proyecto a disposición de las instituciones académicas asociadas y, por otra, darle difusión de carácter industrial, siempre en el marco de las normas acordadas y recomendadas por la OMS.
Sobre el modelado matemático
Intentemos describir con herramientas matemáticas el proceso de la respiración en el ser humano. Comenzaremos con un modelo muy simple, que puede ser visualizado como un sistema físico constituido por un tubo conectado a un globo. Resulta adecuado suponer que el volumen \(V = V(t)\) alcanzado por el globo verifica
$$
R\dot{V} + E(V-V_0) = -P(t) ,
$$
donde \(R\) y \(E\) son constantes positivas características del tubo y el globo considerados. Aquí, \(P = P(t)\) es la presión aplicada al sistema y \(\dot{V}\) denota la derivada temporal de \(V\). Podemos interpretar que el globo es un pulmón, el tubo es la tráquea y \(P\) resulta de la contracción del diafragma y posiblemente los músculos abdominales durante la inspiración. Por ejemplo, si suponemos que \(V(0) = V_0\), entonces
$$
V(t) = V_0 – \frac{1}{R} \int_0^t e^{-\lambda(s-t)} P(s) \,ds , \quad \hbox{ con } \ \lambda = E /R.
$$
Es especialmente interesante analizar el posible comportamiento periódico del sistema. En este sentido, se puede probar que, si \(P\) es \(T\)-periódica, la solución \(V\) es asintóticamente periódica en un sentido adecuado.
Para describir el proceso respiratorio de manera más realista, conviene recurrir a una ley no lineal. En efecto, el modelo precedente admite soluciones con valores de \(V\) arbitrariamente grandes (con \(P\) negativa y de gran valor absoluto), lo que no corresponde a situaciones admisibles. Así, un modelo más apropiado es
$$
R\dot{V} + \varphi(V) = -P(t) ,
$$
donde \(\varphi : (V_m,V_M) \mapsto \mathbf{R}\) es una función regular estrictamente creciente, con \(\varphi(V) \to -\infty\) cuando \(V \to V_m^+\) y \(\varphi(V) \to +\infty\) cuando \(V \to V_M^-\). Un ejemplo adecuado de función \(\varphi\) es
$$
\varphi(V) = \lambda \left( \frac{1}{V_M-V} – \frac{1}{V-V_m} – Z \right),
$$
con
$$
Z = \frac{1}{V_M-V_0} – \frac{1}{V_0-V_m}\,, \ \ \lambda = \frac{E}{ \varphi'(V_0)} \,, \ \ V_0 \in (V_m,V_M).
$$
Para este modelo, se pueden demostrar propiedades «razonables», que concuerdan con el comportamiento observado en el mundo real. Así, si tenemos \(P_0 \leq P(t) \leq P_1\), \(V_0\) y \(V_1\) son los volúmenes asociados respectivamente a \(P_0\) y \(P_1\) (es decir, \(\varphi(V_i) = P_i\)) y elegimos un dato inicial en \((V_0,V_1)\), entonces la solución asociada toma valores también en \((V_0,V_1)\). Por otra parte, si \(P : \mathbf{R} \mapsto \mathbf{R}\) es localmente integrable y \(T\)-periódica, existe una única solución \(T\)-periódica asociada.
En la práctica, para una descripción más precisa, los modelos deben contener muchos más detalles. Entre otras cosas, debemos aceptar que el coeficiente \(R\) que aparece en los modelos precedentes (la resistencia hidráulica del sistema) dependa de \(V\) y \(\dot{V}\). También, debemos imponer características geométricas más complicadas, con la cavidad pulmonar constituida por \(m\) compartimentos distintos. Más precisamente, en vez de una incógnita escalar \(V\), es conveniente considerar una variable \(m\)-valuada \((V_1,\dots,V_m)\) correspondiente a los volúmenes de los distintos compartimentos. El sistema resultante toma la forma
$$
R(V,\dot{V})\dot{V} + \Phi(V) = -(p + P_0(t))\mathbf{e}, \quad \Phi(V) = (\Phi_1(V), \dots,\Phi_m(V)),
$$
donde \(\mathbf{e}\) es un vector cuyas componentes valen \(1\) y las \(\Phi_j\) son similares a la función \(\varphi\) considerada más arriba. Para que la descripción sea lo más completa posible, hemos descompuesto la presión en suma de dos: una presión exterior \(p = p(t)\) (que eventualmente se debe a la acción de un respirador y puede ser interpretada como un control en el sistema) y la presión «natural», antes denotada \(P\).
Otros modelos mucho más detallados (y complicados) pueden conseguirse acoplando estas ecuaciones con sistemas de ecuaciones en derivadas parciales con origen en mecánica de fluidos que describen el flujo sanguíneo.
Para saber más
Para conocer la historia de la compañía Dräger:
- The History of Dräger,
https://www.draeger.com/Library/Content/the_history_of_draeger_2.pdf
Para detalles sobre el respirador HEV:
- J. Buytaert and others, The HEV Ventilator Proposal, CERN-EP-TECH-NOTE-2020-01, April 3, 2020.
Para comprender bien los modelos que describen el proceso respiratorio:
- B. Maury, The Respiratory System in Equations. Modeling, Simulation & Applications, Vol. 7, Springer-Verlag Italia 2013
Otros trabajos recientes de interés:
- P.G.B. Calderon and others, Control aspects of the human cardiovascular-respiratory system under a nonconstant workload. Mathematical Biosciences 289 (2017) 142-152.
- P. Cazeaux, C. Grandmont, Homogenization of a multiscale viscoelastic model with nonlocal damping, application to the human lungs. Mathematical Models and Methods in Applied Sciences Vol. 25, No. 6 (2015) 1125-1177.
- S.P. Hou and others, Adaptive sliding mode control for a general nonlinear multicompartment lung model with input pressure and rate saturation constraints, Int. J. Robust Nonlinear Control 2016: 719-736.
- MR. Owen, M.A. Lewis, The mechanics of lung tissue under high-frequency ventilation, SIAM J. Appl. Math Vol. 61, No. 5, pp. 1731-1761.

Dejar una contestacion