¿Cómo nos infecta un virus?

Aún se desconocen muchos aspectos sobre los mecanismos de infección del coronavirus SARS-CoV-2, pues es un nuevo patógeno para nuestra especie. Sin duda, la elevada cantidad de información que nos llega durante el confinamiento al que estamos sometidos hace que términos como  «carga viral» y «dosis infectiva» se encuentren entre los conceptos que leemos o escuchamos casi a diario. Y, sí, son conceptos para los que las herramientas de modelización matemática pueden ayudar en su descripción. Es más, la modelización ayuda incluso en la generación de valores concretos de estos parámetros, algo que no siempre es fácil en la clínica.

Determinar los valores, o rangos de valores, propios de la carga viral o de la dosis infectiva puede ser de utilidad para la toma de decisiones según los escenarios. Por ejemplo, conocer cuál es el valor de la dosis infectiva con la que el virus sea capaz de evadir la respuesta inmune, es decir, que nuestro organismo no pueda ganarle el combate, o estimar qué pequeñas dosis de virus, y con qué frecuencia y continuidad, puede hacer que se llegue a un umbral tal que dé lugar a que el virus también gane a nuestro sistema inmune. El primer escenario es aquel en el que cualquier persona puede contagiarse tras un solo contacto con otra infectada que, con una elevada carga viral, emita tal cantidad de virus que se garantice que al receptor le llegue la dosis infectiva. El segundo escenario es aquel en el que nos podemos encontrar en el día a día, con pequeñas cantidades de virus que queden en el ambiente o sobre superficies contaminadas, algo de lo que hablamos en otra entrada de este blog.

En concreto, en esta entrada vamos a discutir los conceptos «carga viral» y «dosis infectiva», conceptos muy arraigados en los estudios epidemiológicos, y que necesitan un poco de matemáticas para poder entenderlos en su totalidad.

Así pues, la «carga viral» se define como la cantidad de virus que se encuentra en el interior de la persona infectada, y la «dosis infectiva» es la cantidad mínima de partículas virales necesarias para producir la infección. Está claro que, mientras que la dosis infectiva es un número más o menos concreto que sólo se tiene en cuenta para el inicio de la infección, la carga viral varía a lo largo del proceso, ya que la cantidad de virus aumenta cuando se replica en el interior de las primeras células infectadas y, más aún, conforme las nuevas partículas infectan a otras células del organismo. Por tanto, dicho número (carga viral) puede aumentar hasta acabar con la vida del individuo, o puede ir disminuyendo hasta desaparecer del todo según responda el sistema inmune.

Para el SARS-CoV-2 no se conoce la dosis infectiva  mínima real, ni para la mayoría de los virus, pero se estima que 100 partículas víricas que lleguen a infectar a una o dos células del pulmón (concretamente a las llamas células alveolares de tipo II) pueden ser suficientes para conseguir que el virus se replique e infecte a otras células. A nivel experimental, la dosis infectiva se establece a través del cálculo del TCID50, que es la dosis de virus capaz de infectar al \(50\%\) de los cultivos de células utilizados, y que ya definimos en la citada entrada de este blog.

Por otro lado, la carga viral está directamente relacionada con el número de partículas virales que el individuo infectado puede emitir al hablar, estornudar o toser. Se ha detectado que el número de partículas de coronavirus alcanza un pico a los 5-6 días después de la infección, con valores en el rango de \(10^4-10^7\) partículas por ml. La severidad de los síntomas también suele estar relacionada con la carga viral de modo que los síntomas suelen ser más severos en pacientes con una mayor carga viral.

 ¿Cómo nos infecta un virus?

Hay dos factores que influyen en como un virus nos va a infectar. Una vez que en virus entra en nuestro organismo (normalmente vía boca, nariz y ojos) hay dos procesos que se tienen que considerar:

1. ¿Cuánto tiempo tardan las partículas virales en adherirse y entrar en las células?
2. ¿Cuántas partículas virales entran en nuestras células (pulmonares, por ejemplo)?

Vamos a considerar ambos procesos brevemente:

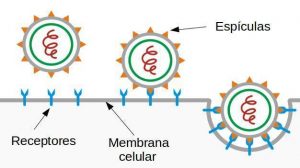
Una vez que el virus entra a través del sistema respiratorio de un individuo, el primer paso de la infección consiste en la unión del virus a la célula (en inglés virus attachment) lo cual, desde un punto de vista físico-matemático, depende de la probabilidad de que el virus y la célula se encuentren y, por lo tanto, de la concentración de ambos (ver página 124 de [1]). Así pues, la tasa \(U\) de unión entre el virus y la célula se puede describir, en una primera aproximación, a través de la ecuación cinética siguiente:
$$
\frac{dU}{dt} = k[V][C] ,
$$
donde \(t\) es el tiempo, \([V]\) y \([C]\) las concentraciones de virus y de células, respectivamente; y \(k\) la constante cinética, que en nuestro caso estará determinada por la intensidad del reconocimiento entre ambos (se sabe que los virus entran por determinadas zonas de las células, y que hay células más proclives a ser infectadas que otras). Es evidente que esta es una representación muy sencilla del proceso de infección, ya que existen múltiples variables de las que va a depender que el virus llegue y encuentre a la molécula receptora específica de la célula adecuada. No obstante, no cabe duda de que es un buen punto de partida para la modelización del proceso de infección. En particular, de la ecuación cinética anterior se deduce que la velocidad de unión entre el virus y las células de su huésped aumenta con la cantidad de partícula virales que entren en su organismo.

Veamos ahora cómo, una vez que el virus se ha unido a la célula, podemos describir de un modo sencillo el impacto de la denominada «multiplicidad de infección» (MOI por sus siglas en inglés); o sea, cuántas partículas infectivas hay por cada célula (ver página 50 de [1]). Por ejemplo, si tenemos un cultivo donde hay \(10^6\) células y \(10^7\) virus, el MOI es 10, y si tenemos \(10^6\) células y \(10^6\) virus, el MOI es 1.

Supongamos que los virus y las células están en suspensión. El que ambos se encuentren dependerá, como ya hemos dicho, de la colisión aleatoria entre ellos. A algunas células no se le unirá virus alguno; a otras uno, o dos o tres, y así hasta el aburrimiento. La probabilidad de que a una célula se le una uno, dos, o más virus (y por tanto que descarguen en ella su material genético) sigue una distribución de Poisson
$$
P(k) = \frac{e^{-m} m^k}{k!} ,
$$
donde \(P(k)\) es la fracción de células infectadas por \(k\) virus y \(m\) es la MOI, que puede calcularse a partir de la proporción de células que no se infectan \(P(0)\) en un experimento controlado. Veámoslo con un ejemplo:

Si \(k\) es cero, entonces \(P(0)\) es la proporción de células que no se infectan y, por lo tanto,
$$
P(0) = e^{-m} \quad \Rightarrow m = -\ln P(0).
$$
Imaginemos que tenemos un cultivo con un MOI\(=10\). Entonces la fracción de células que se infecten por \(0\), \(1\) y más de \(1\) virus, puede obtenerse fácilmente del siguiente modo:

Para fracción de células que no se infectan, \(P(0)\), se tiene
$$
P(0) = e^{-10} = 4,5\cdot 10^{-5} ,
$$
que, en un cultivo de \(10^6\) células, corresponde a 45 células no infectadas, o sea, casi ninguna.

La fracción de células que se infectan con 1 virus, \(P(1)\), será
$$
P(1) = 10\cdot 4,5\cdot 10^{-5} = 4,5\cdot 10^{-5} ,
$$
que, en un cultivo de \(10^6\) células, corresponde a 450 células que se infectan con 1 virus.

La fracción de células que se infectan con más de 1 virus, \(P(>1)\), será, por tanto
$$
P(>1) = 1-P(0)-P(1)=1- e^{-m} \cdot (m+1) = 0,9995,
$$
que, en un cultivo de \(10^6\) células, corresponde a \(999500\), o sea, casi todas las células estarán infectadas por uno o más de 1 virus.

De este modo, si queremos garantizar que el \(99\%\) de las células de un cultivo se infecten, la MOI requerida será
$$
P(0) = 1\% = 0,01 \quad \Rightarrow m = -\ln(0,01) = 4.6.
$$
Conviene hacer notar que es prácticamente imposible conocer el valor del MOI en el caso de un individuo, este es más bien un indicador teórico que nos indica la proporción de cuantas células se infectan y por cuántos virus. De los ejemplos considerados, se tiene además que, si el MOI es alto, entonces la probabilidad de que una gran cantidad de células quede infectada aumenta considerablemente. Por otro lado, si la concentración de virus inicial en nuestras células pulmonares, por ejemplo, es muy alta entonces la tasa de unión es más grande y por tanto los virus pueden penetrar en las células más rápidamente, de modo que podemos contraer más fácilmente la enfermedad.

A modo de conclusión.

Como conclusión, los dos factores discutidos en esta entrada llegamos a que conviene evitar aquellos sitios donde pudiera haber una mayor concentración de virus y, en caso de que no hubiese alternativa, habría que ir convenientemente protegido con mascarillas y guantes y evitar tocarse boca, nariz y ojos. Dado que, como ya se comentó al principio de esta entrada, las personas enfermas de COVID-19 (con o sin no síntomas [2]) suelen tener una alta carga viral (al parecer más alta cuando los síntomas son más severos, pero no necesariamente), y por tanto expulsan mucha mas cantidad de partículas virales al estornudar, toser e incluso al hablar, es de especial importancia que los sanitarios que han de tratarlos extremen sus precauciones y que se les dote de los medios de protección adecuados. Así mismo, cuando comience la desescalada del confinamiento, todos debemos ser conscientes del peligro de contagio y tomar todas las medidas pertinentes.

Finalmente, tenemos que mencionar que lo discutido en esta estrada sólo describe a grandes rasgos como comienza la infección, y es lo suficientemente general como para no tener el cuenta el modo concreto de entrada del virus en las células (en el caso del SARS-CoV-2, como en el resto de los coronavirus es mediante la endocitosis [3] cuyo esquema podemos ver en la figura 1). Si queremos describir como se desarrolla la misma en el interior del organismo necesitamos modelos dinámicos más complejos. Intentaremos en una próxima entrada presentar algunos de los posibles modelos matemáticos que nos permitan describir e interpretar como se desarrolla una infección vírica en nuestro organismo.

Si quieres bajarte el pdf de la entrada pincha AQUÍ.

Bibliografía

[1] S. Jane Flint, Vincent R. Racaniello, Glenn F. Rall, Anna Marie Skalka, Lynn W. Enquist, Principles of Virology, 3º ed., Vol 1. American Society for Microbiology Press, Washington DC, 2015.

[2] Monica Gandhi, Deborah S. Yokoe, and Diane V. Havlir, Asymptomatic Transmission, the Achilles’ Heel of Current Strategies to Control Covid-19,
The New England Journal of Medicine, April 24, 2020. DOI: 10.1056/NEJMe2009758

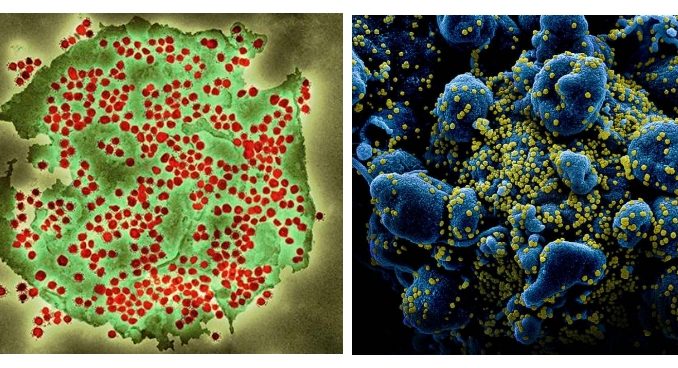
[3] Fuente de las fotos de la figura 2. Izquierda: Coloured transmission electron micrograph (TEM) of a SARS-CoV-2 coronavirus particle isolated from a UK case of the disease Covid-19. SARS-CoV-2 (https://publichealthmatters.blog.gov.uk}). Derecha: Colorized scanning electron micrograph of an apoptotic cell (blue) heavily infected with SARS-COV-2 virus particles (yellow), isolated from a patient sample. Image captured and color-enhanced at the NIAID Integrated Research Facility (IRF) in Fort Detrick, Maryland. Credit: NIAID (https://www.flickr.com/photos/niaid/)